6.5: Closure Operations on Relations
- Page ID
- 80525
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Section 6.1, we studied relations and one important operation on relations, namely composition. This operation enables us to generate new relations from previously known relations. In Section 6.3, we discussed some key properties of relations. We now wish to consider the situation of constructing a new relation \(r^+\) from an existing relation \(r\) where, first, \(r^+\) contains \(r\) and, second, \(r^{+ }\) satisfies the transitive property.
Transitive Closure
Consider a telephone network in which the main office \(a\) is connected to, and can communicate to, individuals \(b\) and \(c\text{.}\) Both \(b\) and \(c\) can communicate to another person, \(d\text{;}\) however, the main office cannot communicate with \(d\text{.}\) Assume communication is only one way, as indicated. This situation can be described by the relation \(r = \{(a, b), (a, c), (b, d), (c, d)\}\text{.}\) We would like to change the system so that the main office \(a\) can communicate with person \(d\) and still maintain the previous system. We, of course, want the most economical system.
This can be rephrased as follows; Find the smallest relation \(r^{+ }\) which contains \(r\) as a subset and which is transitive; \(r^+ =\{(a, b), (a, c), (b, d), (c, d), (a, d)\}\text{.}\)
Definition \(\PageIndex{1}\): Transitive Closure
Let \(A\) be a set and \(r\) be a relation on \(A\text{.}\) The transitive closure of \(r\text{,}\) denoted by \(r^+\text{,}\) is the smallest transitive relation that contains \(r\) as a subset.
Let \(A = \{1, 2, 3, 4\}\text{,}\) and let \(\mathcal{S} = \{(1, 2), (2, 3), (3, 4)\}\) be a relation on \(A\text{.}\) This relation is called the successor relation on \(A\) since each element is related to its successor. How do we compute \(\mathcal{S}^+\text{?}\) By inspection we note that \((1, 3)\) must be in \(\mathcal{S}^+\) . Let's analyze why. This is so because \((1,2) \in \mathcal{S}\) and \((2, 3) \in \mathcal{S}\text{,}\) and the transitive property forces \((1,3)\) to be in \(\mathcal{S}^+\text{.}\)
In general, it follows that if \((a, b) \in \mathcal{S}\) and \((b, c) \in S,\) then \((a, c) \in \mathcal{S}^+ \text{.}\) This condition is exactly the membership requirement for the pair \((a, c)\) to be in the composition \(\mathcal{S}\mathcal{S} = \mathcal{S}^2\text{.}\) So every element in \(\mathcal{S}^2\) must be an element in \(\mathcal{S}^+\) . So we now know that, \(\mathcal{S}^+\) contains at least \(\mathcal{S} \cup \mathcal{S}^2\) . In particular, for this example, since \(\mathcal{S} = \{(1, 2), (2, 3), (3, 4)\}\) and \(\mathcal{S}^2 = \{(1, 3), (2, 4)\}\text{,}\) we have
\begin{equation*} \mathcal{S} \cup \mathcal{S}^2 =\{(1, 2), (2, 3), (3, 4), (1, 3), (2, 4)\} \end{equation*}
Is the relation \(\mathcal{S} \cup \mathcal{S}^2\) transitive? Again, by inspection, \((1, 4)\) is not an element of \(\mathcal{S} \cup \mathcal{S}^2\text{,}\) but \((1,3) \in \mathcal{S}^2\) and \((3, 4) \in \mathcal{S}\text{.}\) Therefore, the composition \(\mathcal{S}^2 \mathcal{S} = \mathcal{S}^3\) produces \((1, 4)\text{,}\) and it must be an element of \(\mathcal{S}^+\) since \((1,3)\) and \((3, 4)\) are required to be in \(\mathcal{S}^+\text{.}\) This shows that \(\mathcal{S}^3 \subseteq \mathcal{S}^+\text{.}\) This process must be continued until the resulting relation is transitive. If \(A\) is finite, as is true in this example, the transitive closure will be obtained in a finite number of steps. For this example,
\begin{equation*} \mathcal{S}^+ =\mathcal{S}\cup \mathcal{S} ^2\cup \mathcal{S} ^3=\{(1, 2), (2, 3), (3, 4),(1, 3),(2, 4),(1,4)\} \end{equation*}
Theorem \(\PageIndex{1}\): Transitive Closure on a Finite Set
If \(r\) is a relation on a set \(A\) and \(\lvert A \rvert = n\text{,}\) then the transitive closure of \(r\) is the union of the first \(n\) powers of r. That is,
\begin{equation*} r^+ = r \cup r^2 \cup r ^3 \cup \cdots \cup r^n\text{.} \end{equation*}
Let's now consider the matrix analogue of the transitive closure.
Consider the relation
\begin{equation*} r = \{(1, 4), (2, 1), (2, 2), (2, 3),(3, 2), (4, 3), (4, 5), (5, 1)\} \end{equation*}
on the set \(A = \{1,2, 3, 4, 5\}\text{.}\) The matrix of \(r\) is
\begin{equation*} R=\left( \begin{array}{ccccc} 0 & 0 & 0 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ \end{array} \right) \end{equation*}
Recall that \(r^2, r^3, \ldots\) can be determined through computing the matrix powers \(R^2, R^3, \ldots\text{.}\) For our example,
Table \(\PageIndex{1}\)
| \(R^2=\left( \begin{array}{ccccc} 0 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ \end{array} \right)\) | \(R^3=\left( \begin{array}{ccccc} 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ \end{array} \right)\) |
| \(R^4=\left( \begin{array}{ccccc} 1 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 & 0 \\ \end{array} \right)\) | \(R^5=\left( \begin{array}{ccccc} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 \\ \end{array} \right)\) |
How do we relate \(\underset{i=1}{\overset{5}{\cup }}r^i\) to the powers of \(R\text{?}\)
Theorem \(\PageIndex{2}\): Matrix of a Transitive Closure
Let \(r\) be a relation on a finite set and \(R\) its matrix. Let \(R^+\) be the matrix of \(r^+\text{,}\) the transitive closure of \(r\text{.}\) Then \(R^+ = R + R^2 + \cdots + R^n\text{,}\) using Boolean arithmetic.
Using this theorem, we find \(R^+\) is the \(5\times 5\) matrix consisting of all \(1's\text{,}\) thus, \(r^+\) is all of \(A \times A\text{.}\)
Algorithms for computing transitive closure
Let \(r\) be a relation on the set \(\{1, 2, \dots , n\}\) with relation matrix \(R\text{.}\) The matrix of the transitive closure \(R^+\text{,}\) can be computed by the equation \(R^+ = R + R ^2 + \cdots + R^n\text{.}\) By using ordinary polynomial evaluation methods, you can compute \(R^+\) with \(n -1\) matrix multiplications:
\begin{equation*} R^+ = R(I + R(I +( \cdots R(I+ R) \cdots ))) \end{equation*}
For example, if \(n = 3\text{,}\) \(R^+ = R(I + R(I + R))\text{.}\)
We can make use of the fact that if \(T\) is a relation matrix, \(T + T = T\) due to the fact that \(1 + 1 = 1\) in Boolean arithmetic. Let \(S_k = R + R^2 + \cdots + R^k\text{.}\) Then
\begin{equation*} \begin{split} R &= S_1\\ S_1(I+S_1)&=R(I+R)=R+R^2 = S_2 \\ S_2(I+S_2)&=(R+R^2)(I+R+R^2) \\ &=(R+R^2)+(R^2+R^3)+(R^3+R^4) \\ &=R+R^2+R^3+R^4 = S_4 \end{split}\text{.} \end{equation*}
Similarly,
\begin{equation*} S_4(I+S_4)=S_8 \end{equation*}
and by induction we can prove
\begin{equation*} S_{2^k}(I+S_{2^k})=S_{2^{k+1}} \end{equation*}
Notice how each matrix multiplication doubles the number of terms that have been added to the sum that you currently have computed. In algorithmic form, we can compute \(R^+\) as follows.
Algorithm \(\PageIndex{1}\): Transitive Closure Algorithm
Let \(R\) be a relation matrix and let \(R^+\) be its transitive closure matrix, which is to be computed as matrix \(T\)
1.0. S=R
2.0 T=S*(I+S)
3.0 While T != S
3.1 S = T
3.2 T= S*(I+S) // using Boolean arithmetic
4.0 Return T
Listing \(\PageIndex{1}\)
Note \(\PageIndex{1}\)
- Often the higher-powered terms in \(S_{n}\) do not contribute anything to \(R^{+}\). When the condition \(T=S\) becomes true in Step 3, this is an indication that no higher-powered terms are needed.
- To compute \(R^{+}\) using this algorithm, you need to perform no more than \(⌈\log_{2}n⌉\) matrix multiplications, where \(⌈x⌉\) is the least integer that is greater than or equal to \(x\). For example, if \(r\) is a relation on 25 elements, no more than \(⌈\log_{2}25⌉=5\) matrix multiplications are needed.
A second algorithm, Warshall's Algorithm, reduces computation time to the time that it takes to multiply two square matrices with the same order as the relation matrix in question.
Algorithm \(\PageIndex{2}\): Warshall's Algorithm
Let \(R\) be an \(n \times n\) relation matrix and let \(R^+\) be its transitive closure matrix, which is to be computed as matrix \(T\) using Boolean arithmetic
1.0 T = R
2.0 for k = 1 to n:
for i = 1 to n:
for j = 1 to n:
T[i,j]= T[i,j] + T[i,k] * T[k,j]
3.0 Return T
Listing \(\PageIndex{2}\)
Exercises
Exercise \(\PageIndex{1}\)
Let \(A =\{0, 1, 2, 3, 4\}\) and \(\mathcal{S}=\{(0, 1), (1, 3), (2, 3), (3, 4), (4, 1)\}\text{.}\) Compute \(\mathcal{S}^+\) using the matrix representation of \(\mathcal{S}\text{.}\) Verify your results by checking against the result obtained directly from the definition of transitive closure.
Exercise \(\PageIndex{2}\)
Let \(A=\{1,2,3,4,6,12\}\) and \(t=\{(a,b)\mid b/a \textrm{ is a prime number}\}\text{.}\) Determine \(t^+\) by any means. Represent your answer as a matrix.
Exercise \(\PageIndex{3}\)
- Draw digraphs of the relations \(\mathcal{S}\text{,}\) \(\mathcal{S}^2\text{,}\) \(\mathcal{S}^3\) , and \(\mathcal{S}^+\) where \(\mathcal{S}\) is defined in the first exercise above.
- Verify that in terms of the graph of \(\mathcal{S}\text{,}\) \(a \mathcal{S}^+ b\) if and only if \(b\) is reachable from \(a\) along a path of any finite nonzero length.
- Answer
-
- See graphs below.
- For example, \(0 s^+ 4\) and using \(S\) one can go from 0 to 4 using a path of length 3.
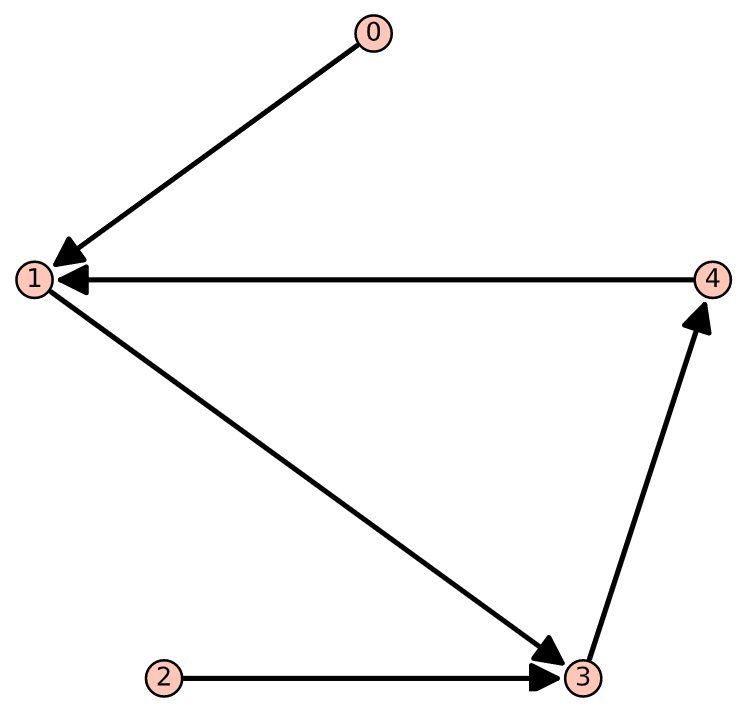
Figure \(\PageIndex{1}\): Digraph of \(S\)
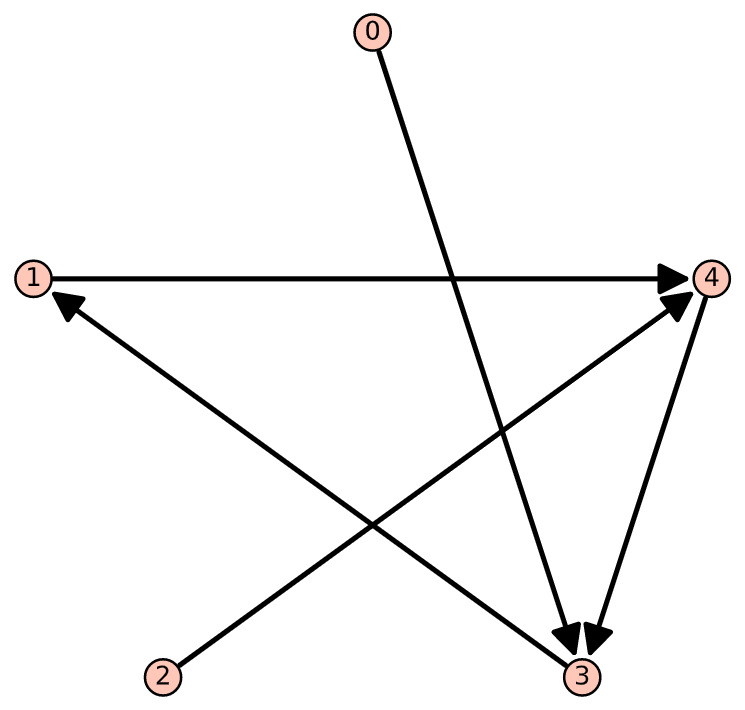
Figure \(\PageIndex{2}\): Digraph of \(S^{2}\)
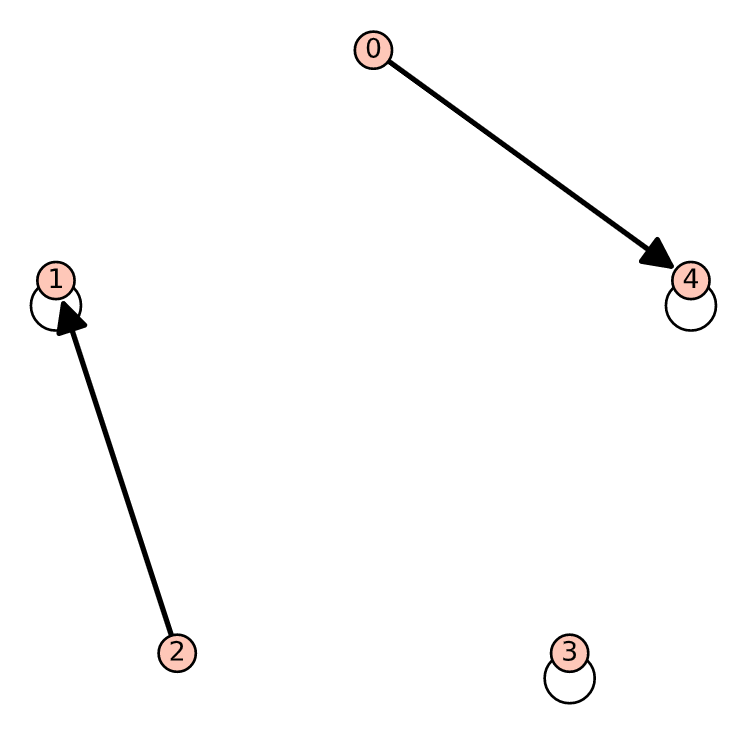
Figure \(\PageIndex{3}\): Digraph of \(S^{3}\)
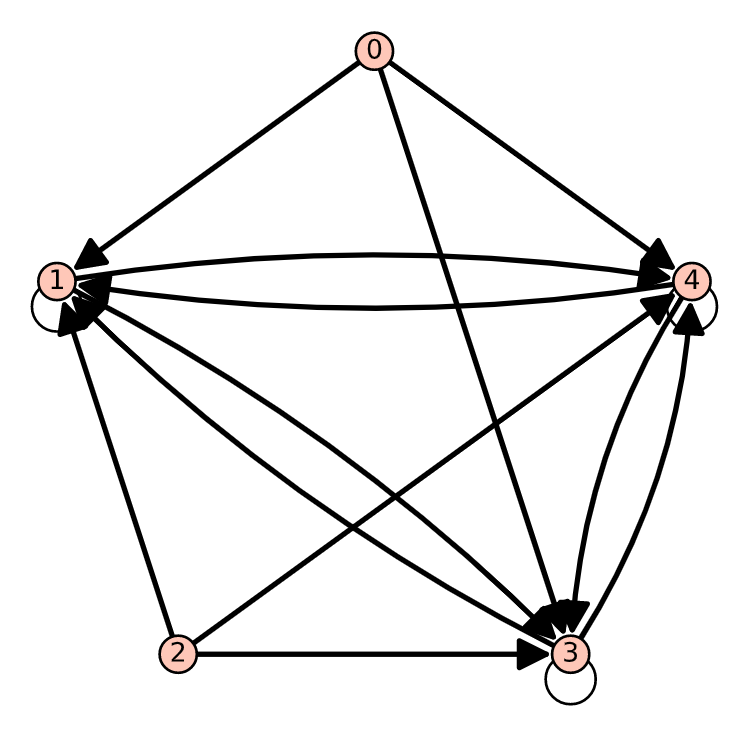
Figure \(\PageIndex{4}\): Digraph of \(S^{+}\)
Exercise \(\PageIndex{4}\)
Let \(r\) be the relation represented by the following digraph.
- Find \(r^+\) using the definition based on order pairs.
- Determine the digraph of \(r^+\) directly from the digraph of \(r\text{.}\)
- Verify your result in part (b) by computing the digraph from your result in part (a).
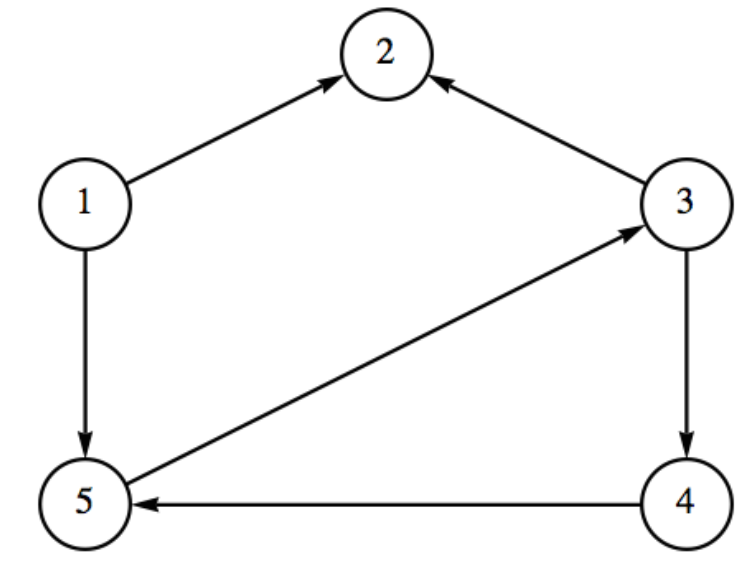
Figure \(\PageIndex{5}\): Digraph of \(r\) in Exercise \(\PageIndex{4}\)
Exercise \(\PageIndex{5}\)
- Define reflexive closure and symmetric closure by imitating the definition of transitive closure.
- Use your definitions to compute the reflexive and symmetric closures of examples in the text.
- What are the transitive reflexive closures of these examples?
- Convince yourself that the reflexive closure of the relation \(<\) on the set of positive integers \(\mathbb{P}\) is \(\leq\text{.}\)
- Answer
-
Definition: Reflexive Closure. Let \(r\) be a relation on \(A\text{.}\) The reflexive closure of \(r\) is the smallest reflexive relation that contains \(r\text{.}\)
Theorem: The reflexive closure of \(r\) is the union of \(r\) with \(\{(x, x) : x\in A\}\)
Exercise \(\PageIndex{6}\)
What common relations on \(\mathbb{Z}\) are the transitive closures of the following relations?
- \(a S b\) if and only if \(a + 1 = b\text{.}\)
- \(a R b\) if and only if \(| a - b | = 2\text{.}\)
Exercise \(\PageIndex{7}\)
- Let \(A\) be any set and \(r\) a relation on \(A\text{,}\) prove that \(\left(r^+\right)^+=r^+\text{.}\)
- Is the transitive closure of a symmetric relation always both symmetric and reflexive? Explain.
- Answer
-
- By the definition of transitive closure, \(r^+\) is the smallest relation which contains \(r\text{;}\) therefore, it is transitive. The transitive closure of \(r^+\text{,}\) \(\left(r^+\right)^+\) , is the smallest transitive relation that contains \(r^+\text{.}\) Since \(r^+\) is transitive, \(\left(r^+\right)^+=r^+\text{.}\)
- The transitive closure of a symmetric relation is symmetric, but it may not be reflexive. If one element is not related to any elements, then the transitive closure will not relate that element to others.
Exercise \(\PageIndex{8}\)
The definition of the Transitive Closure, Definition \(\PageIndex{1}\), of \(r\) refers to the “smallest transitive relation that contains \(r\) as a subset.” Show that the intersection of all transitive relations on \(A\) containing \(r\) is a transitive relation containing \(r\) and is precisely \(r^+\text{.}\)


