12.3: Paths and Cycles

Recall the definition of a walk. As we saw in Example 12.2.1, the vertices and edges in a walk do not need to be distinct.

There are many circumstances under which we might not want to allow edges or vertices to be re-visited. Efficiency is one possible reason for this. We have a special name for a walk that does not allow vertices to be re-visited.

Definition: Path

A walk in which no vertex appears more than once is called a path.

Notation

For $n ≥ 0$, a graph on $n + 1$ vertices whose only edges are those used in a path of length $n$ (which is a walk of length $n$ that is also a path) is denoted by $P_n$. (Notice that $P_0 \cong K_1$ and $P_1 \cong K_2$.)

Notice that if an edge were to appear more than once in a walk, then both of its endvertices would also have to appear more than once, so a path does not allow vertices or edges to be re-visited.

Example $\PageIndex{1}$

In the graph

$(a, f, c, h)$ is a path of length $3$. However, $(a, f, c, h, d, f)$ is not a path, even though no edges are repeated, since the vertex $f$ appears twice. Both are walks.

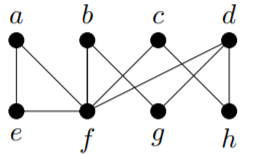
Proposition $\PageIndex{1}$

Suppose that $u$ and $v$ are in the same connected component of a graph. Then any $u − v$ walk of minimum length is a path. In particular, if there is a $u − v$ walk, then there is a $u − v$ path.

Proof

Since $u$ and $v$ are in the same connected component of a graph, there is a $u − v$ walk.

Towards a contradiction, suppose that we have a $u − v$ walk of minimum length that is not a path. By the definition of a path, this means that some vertex $x$ appears more than once in the walk, so the walk looks like:

$$(u = u_1, . . . , u_i = x, . . . , u_j = x, . . . , u_k = v),$$

and $j > i$. Observe that the following is also a $u − v$ walk:

$$(u = u_1, . . . , u_i = x, u_{j+1}, u_{j+2}, . . . , u_k = v).$$

Since consecutive vertices were adjacent in the first sequence, they are also adjacent in the second sequence, so the second sequence is a walk. The length of the first walk is $k − 1$, and the length of the second walk is $k − 1 − (j − i)$. Since $j > i$, the second walk is strictly shorter than the first walk. In particular, the first walk was not a $u − v$ walk of minimum length. This contradiction serves to prove that every $u − v$ walk of minimum length is a path.

This allows us to prove another interesting fact that will be useful later.

Proposition $\PageIndex{2}$

Deleting an edge from a connected graph can never result in a graph that has more than two connected components.

Proof

Let $G$ be a connected graph, and let $u_v$ be an arbitrary edge of $G$. If $G \setminus \{u_v\}$ is connected, then it has only one connected component, so it satisfies our desired conclusion. Thus, we assume in the remainder of the proof that $G \setminus \{u_v\}$ is not connected.

Let $G_u$ denote the connected component of $G \setminus \{u_v\}$ that contains the vertex $u$, and let $G_v$ denote the connected component of $G \setminus \{u_v\}$ that contains the vertex $v$. We aim to show that $G_u$ and $G_v$ are the only connected components of $G \setminus \{u_v\}$.

Let $x$ be an arbitrary vertex of $G$, and suppose that $x$ is a vertex that is not in $G_u$. Since $G$ is connected, there is a $u − x$ walk in $G$, and therefore by Proposition 12.3.1 there is a $u − x$ path in $G$. Since $x$ is not in $G_u$, this $u−x$ path must use the edge $u−v$, so must start with this edge since $u$ only occurs at the start of the path. Therefore, by removing the vertex $u$ from the start of this path, we obtain a $v − x$ path that does not use the vertex $u$. This path cannot use the edge $u_v$, so must still be a path in $G \setminus \{u_v\}$. Therefore $x$ is a vertex in $G_v$.

Since $x$ was arbitrary, this shows that every vertex of $G$ must be in one or the other of the connected components $G_u$ and $G_v$, so there are at most two connected components of $G \setminus \{u_v\}$. Since $u_v$ was an arbitrary edge of $G$ and $G$ was an arbitrary connected graph, this shows that deleting any edge of a connected graph can never result in a graph with more than two connected components.

A cycle is like a path, except that it starts and ends at the same vertex. The structures that we will call cycles in this course, are sometimes referred to as circuits.

Definition: Cycle

A walk of length at least $1$ in which no vertex appears more than once, except that the first vertex is the same as the last, is called a cycle.

Notation

For $n ≥ 3$, a graph on $n$ vertices whose only edges are those used in a cycle of length $n$ (which is a walk of length $n$ that is also a cycle) is denoted by $C_n$.

The requirement that the walk have length at least $1$ only serves to make it clear that a walk of just one vertex is not considered a cycle. In fact, a cycle in a simple graph must have length at least $3$.

Example $\PageIndex{2}$

In the graph from Example 12.3.1, $(a, e, f, a)$ is a cycle of length $3$, and $(b, g, d, h, c, f, b)$ is a cycle of length $6$.

Here are drawings of some small paths and cycles:

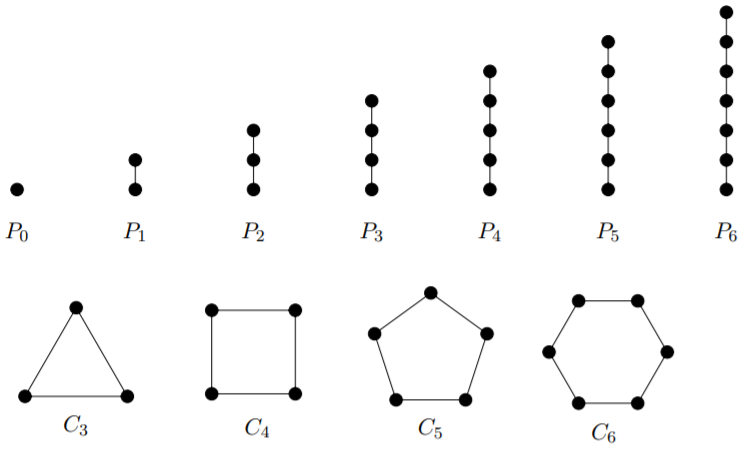
We end this section with a proposition whose proof will be left as an exercise.

Proposition $\PageIndex{3}$

Suppose that $G$ is a connected graph. If $G$ has a cycle in which $u$ and $v$ appear as consecutive vertices (so $u_v$ is an edge of $G$) then $G \setminus \{u_v\}$ is connected.

Exercise $\PageIndex{1}$

1) In the graph

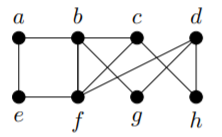
(a) Find a path of length $3$.

(b) Find a cycle of length $3$.

(c) Find a walk of length $3$ that is neither a path nor a cycle. Explain why your answer is correct.

2) Prove that in a graph, any walk that starts and ends with the same vertex and has the smallest possible non-zero length, must be a cycle.

3) Prove Proposition 12.3.3.

4) Prove by induction that if every vertex of a connected graph on $n ≥ 2$ vertices has valency $1$ or $2$, then the graph is isomorphic to $P_n$ or $C_n$.

5) Let $G$ be a (simple) graph on $n$ vertices. Suppose that $G$ has the following property: whenever $u \nsim v$, $dG(u) + dG(v) ≥ n − 1$. Prove that $G$ is connected.