12.2: Walks and Connectedness
- Page ID
- 60134
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Graphs can be connected or disconnected. Intuitively, this corresponds to the network being connected or disconnected – is it possible to travel from any node to any other node? When a graph (or network) is disconnected, it has broken down into some number of separate connected components - the pieces that still are connected.
Since this is mathematics, we require more formal definitions, to ensure that the meanings are not open to misunderstanding. Before we can define connectedness, we need the concept of a walk in a graph.
Definition: Walk
A walk in a graph \(G\) is a sequence of vertices \((u_1, u_2, . . . , u_n)\) such that for every \(1 ≤ i ≤ n − 1\), we have \(u_i ∼ u_{i+1}\). (That is, consecutive vertices in the walk must be adjacent.)
A \(u − v\) walk in \(G\) is a walk with \(u_1 = u\) and \(u_n = v\). (That is, a walk that begins at \(u\) and ends at \(v\).)
Now we can define what it means for a graph to be connected.
Definition: Word
The graph \(G\) with vertex set \(V\) is connected if for every \(u\), \(v ∈ V\), there is a \(u − v\) walk.
The connected component of \(G\) that contains the vertex \(u\), is
\[\{v ∈ V | \text{ there is a } u − v \text{ walk.}\}\]
This definition of connected component seems to depend significantly on the choice of the vertex \(u\). In fact, though, being in the same connected component of \(G\) is an equivalence relation on the vertices of \(G\), so the connected components of \(G\) are a property of \(G\) itself, rather than depending on particular choices of vertices. We won’t go through a formal proof that being in the same connected component is an equivalence relation (we leave this as an exercise below), but we will go through the proof of a proposition that is closely related.
Proposition \(\PageIndex{1}\)
Let \(G\) be a graph, and let \(u\), \(v\), \(w ∈ V (G)\). Suppose that \(v\) and \(w\) are in the connected component of \(G\) that contains the vertex \(u\). Then \(w\) is in the connected component of \(G\) that contains the vertex \(v\).
- Proof
-
Since \(v\) and \(w\) are in the connected component of \(G\) that contains the vertex \(u\), by definition there is a \(u − v\) walk, and a \(u − w\) walk. Let \((u = u_1, u_2, . . . , u_k = w)\) be a \(u − w\) walk, and let \((u = v_1, v_2, . . . , v_m = v)\) be a \(u − v\) walk.
We need to show that \(w\) is in the connected component of \(G\) that contains the vertex \(v\); by definition, this is equivalent to showing that there is a \(v − w\) walk. Consider the sequence of vertices:
\[(v = v_m, v_{m−1}, . . . , v_1 = u = u_1, u_2, . . . , u_k = w).\]
Since \((u = v_1, v_2, . . . , v_m = v)\) is a \(u − v\) walk, consecutive vertices are adjacent, so consecutive vertices in the first part of the given sequence (from \(v_m\) through \(v_1 = u\)) are adjacent. Similarly, since \((u = u_1, u_2, . . . , u_k = w)\) is a \(u − w\) walk, consecutive vertices are adjacent, so consecutive vertices in the last part of the given sequence (from \(u = u_1\) through \(u_k\)) are adjacent. Therefore, the given sequence is in fact a \(v − w\) walk, as desired.
When discussing walks, it is convenient to have standard terminology for describing the length of the walk.
Definition: Length of a Walk
The length of a walk is one less than the number of vertices in the walk. Thus, if we think of a walk as a sequence of edges (formed by consecutive pairs of vertices from the walk), the length of the walk is the number of edges in the walk.
Unfortunately, there is some disagreement amongst mathematicians as to whether the length of a walk should be used to mean the number of vertices in the walk, or the number of edges in the walk. We will use the latter convention throughout this course because it is consistent with the definition of the length of a cycle (which will be introduced in the next section). You should be aware, though, that you might find the other convention used in other sources.
Sometimes it is obvious that a graph is disconnected from the way it has been drawn, but sometimes it is less obvious. In the following example, you might not immediately notice whether or not the graph is connected.
Example \(\PageIndex{1}\)
Consider the following graph.
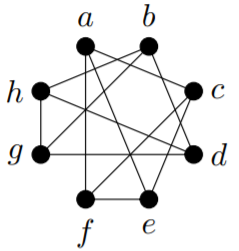
Find \(a\) walk of length \(4\) from \(a\) to \(f\). Find the connected component that contains \(a\). Is the graph connected?
Solution
A walk from of length \(4\) from \(a\) to \(f\) is \((a, c, a, c, f)\). (Notice that the vertices and edges used in a walk need not be distinct.) Remember that the length of this walk is the number of edges used, which is one less than the number of vertices in the sequence!
The connected component that contains \(a\) is \(\{a, c, e, f\}\). There are walks from \(a\) to each of these vertices, but there are no edges between any of these vertices and any of the vertices \(\{b, d, g, h\}\).
Since there is no walk from \(a\) to \(b\) (for example), the graph is not connected.
Exercise \(\PageIndex{1}\)
1) Prove that being in the same connected component of \(G\) is an equivalence relation on the vertices of any graph \(G\).
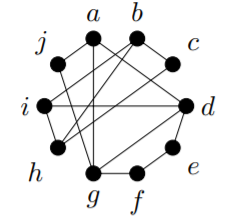
2) Is the following graph connected? Find the connected component that contains \(a\). Find a walk of length \(5\) from \(a\) to \(f\).
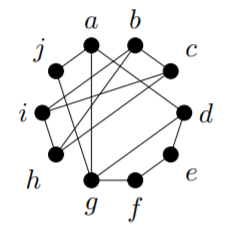
3) Is the following graph connected? Find the connected component that contains \(a\). Find a walk of length \(3\) from \(a\) to \(d\).
4) Use Euler’s Handshaking Lemma to prove (by contradiction) that if \(G\) is a connected graph with \(n\) vertices and \(n − 1\) edges, and \(n ≥ 2\), then \(G\) has at least \(2\) vertices of valency \(1\).
[Hint: What does \(G\) being connected imply about \(d(v)\) for any vertex \(v\) of \(G\)?]
5) Fix \(n ≥ 1\). Prove by induction on \(m\) that for any \(m ≥ 0\), a graph with \(n\) vertices and \(m\) edges has at least \(n − m\) connected components.


