4.6: Matchings
- Page ID
- 7164
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Now we return to systems of distinct representatives.
A system of distinct representatives corresponds to a set of edges in the corresponding bipartite graph that share no endpoints; such a collection of edges (in any graph, not just a bipartite graph) is called a matching. In Figure \(\PageIndex{1}\), a matching is shown in red. This is a largest possible matching, since it contains edges incident with all four of the top vertices, and it thus corresponds to a complete sdr.
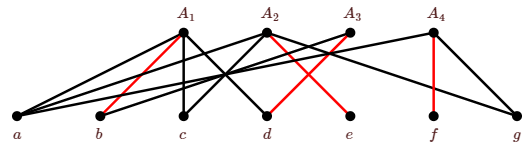
Any bipartite graph can be interpreted as a set system: we simply label all the vertices in one part with "set names'' \(A_1\), \(A_2\), etc., and the other part is labeled with "element names'', and the sets are defined in the obvious way: \(A_i\) is the neighborhood of the vertex labeled "\(A_i\)''. Thus, we know one way to compute the size of a maximum matching, namely, we interpret the bipartite graph as a set system and compute the size of a maximum sdr; this is the size of a maximum matching.
We will see another way to do this working directly with the graph. There are two advantages to this: it will turn out to be more efficient, and as a by-product it will actually find a maximum matching.
Given a bipartite graph, it is easy to find a maximal matching, that is, one that cannot be made larger simply by adding an edge: just choose edges that do not share endpoints until this is no longer possible. See Figure \(\PageIndex{2}\) for an example.
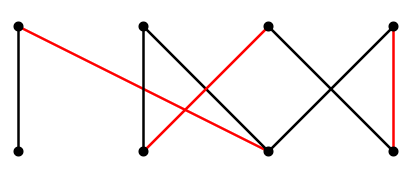
An obvious approach is then to attempt to make the matching larger. There is a simple way to do this, if it works: We look for an alternating chain, defined as follows.
Suppose \(M\) is a matching, and suppose that \(v_1,w_1,v_2,w_2,\ldots,v_k,w_k\) is a sequence of vertices such that no edge in \(M\) is incident with \(v_1\) or \(w_k\), and moreover for all \(1\le i\le k\), \(v_i\) and \(w_i\) are joined by an edge not in \(M\), and for all \(1\le i\le k-1\), \(w_i\) and \(v_{i+1}\) are joined by an edge in \(M\). Then the sequence of vertices together with the edges joining them in order is an alternating chain.
The graph in Figure \(\PageIndex{2}\) contains alternating chains, one of which is shown in Figure \(\PageIndex{3}\).
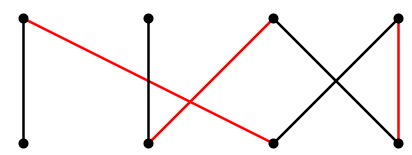
Suppose now that we remove from \(M\) all the edges that are in the alternating chain and also in \(M\), forming \(M'\), and add to \(M'\) all of the edges in the alternating chain not in \(M\), forming \(M''\). It is not hard to show that \(M''\) is a matching, and it contains one more edge than \(M\). See Figure \(\PageIndex{4}\).
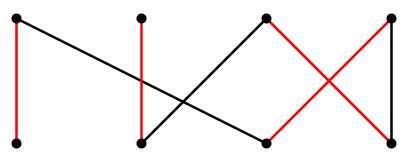
Remarkably, if there is no alternating chain, then the matching \(M\) is a maximum matching.
Suppose that \(M\) is a matching in a bipartite graph \(G\), and there is no alternating chain. Then \(M\) is a maximum matching.
- Proof
-
We prove the contrapositive: Suppose that \(M\) is not a maximum matching. Then there is a larger matching, \(N\). Create a new graph \(G'\) by eliminating all edges that are in both \(M\) and \(N\), and also all edges that are in neither. We are left with just those edges in \(M\) or \(N\) but not both.
In this new graph no vertex is incident with more than two edges, since if \(v\) were incident with three edges, at least two of them would belong to \(M\) or two would belong to \(N\), but that can't be true since \(M\) and \(N\) are matchings. This means that \(G'\) is composed of disjoint paths and cycles. Since \(N\) is larger than \(M\), \(G'\) contains more edges from \(N\) than from \(M\), and therefore one of the paths starts and ends with an edge from \(N\), and along the path the edges alternate between edges in \(N\) and edges in \(M\). In the original graph \(G\) with matching \(M\), this path forms an alternating chain. The "alternating'' part is clear; we need to see that the first and last vertices in the path are not incident with any edge in \(M\).
Suppose that the first two vertices are \(v_1\) and \(v_2\). Then \(v_1\) and \(v_2\) are joined by an edge of \(N\). Suppose that \(v_1\) is adjacent to a vertex \(w\) and that the edge between \(v_1\) and \(w\) is in \(M\). This edge cannot be in \(N\), for then there would be two edges of \(N\) incident at \(v_1\). But then this edge is in \(G'\), since it is in \(M\) but not \(N\), and therefore the path in \(G'\) does not start with the edge in \(N\) joining \(v_1\) and \(v_2\). This contradiction shows that no edge of \(M\) is incident at \(v_1\). The proof that the last vertex in the path is likewise not incident with an edge of \(M\) is essentially identical.
Now to find a maximum matching, we repeatedly look for alternating chains; when we cannot find one, we know we have a maximum matching. What we need now is an efficient algorithm for finding the alternating chain.
The key, in a sense, is to look for all possible alternating chains simultaneously. Suppose we have a bipartite graph with vertex partition \(\{v_1,v_2,\ldots,v_n\}\) and \(\{w_1,w_2,\ldots,w_m\}\) and a matching \(M\). The algorithm labels vertices in such a way that if it succeeds, the alternating chain is indicated by the labels. Here are the steps:
- Label with '(S,0)' all vertices \(v_i\) that are not incident with an edge in \(M\). Set variable step to 0.
Now repeat the next two steps until no vertex acquires a new label: - Increase step by 1. For each newly labeled vertex \(v_i\), label with \((i,step)\) any unlabeled neighbor \(w_j\) of \(v_i\) that is connected to \(v_i\) by an edge that is not in \(M\).
- Increase step by 1. For each newly labeled vertex \(w_i\), label with \((i,step)\) any unlabeled neighbor \(v_j\) of \(w_i\) that is connected to \(w_i\) by an edge in \(M\).
Here "newly labeled'' means labeled at the previous step. When labeling vertices in step 1 or 2, no vertex is given more than one label. For example, in step 1, it may be that \(w_k\) is a neighbor of the newly labeled vertices \(v_i\) and \(v_j\). One of \(v_i\) and \(v_j\), say \(v_i\), will be considered first, and will cause \(w_k\) to be labeled; when \(v_j\) is considered, \(w_k\) is no longer unlabeled.
At the conclusion of the algorithm, if there is a labeled vertex \(w_i\) that is not incident with any edge of \(M\), then there is an alternating chain, and we say the algorithm succeeds. If there is no such \(w_i\), then there is no alternating chain, and we say the algorithm fails. The first of these claims is easy to see: Suppose vertex \(w_i\) is labeled \((k_1,s)\). It became labeled due to vertex \(v_{k_1}\) labeled \((k_2,s-1)\) that is connected by an edge not in \(M\) to \(w_i\). In turn, \(v_{k_1}\) is connected by an edge in \(M\) to vertex \(w_{k_2}\) labeled \((k_3,s-2)\). Continuing in this way, we discover an alternating chain ending at some vertex \(v_j\) labeled \((S,0)\): since the second coordinate step decreases by 1 at each vertex along the chain, we cannot repeat vertices, and must eventually get to a vertex with \(step=0\). If we apply the algorithm to the graph in Figure \(\PageIndex{2}\), we get the labeling shown in Figure \(\PageIndex{5}\), which then identifies the alternating chain \(w_2, v_3,w_1,v_1\). Note that as soon as a vertex \(w_i\) that is incident with no edge of \(M\) is labeled, we may stop, as there must be an alternating chain starting at \(w_i\); we need not continue the algorithm until no more labeling is possible. In the example in Figure \(\PageIndex{5}\), we could stop after step 3, when \(w_2\) becomes labeled. Also, the step component of the labels is not really needed; it was included to make it easier to understand that if the algorithm succeeds, there really is an alternating chain.
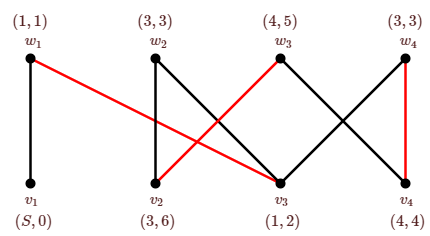
To see that when the algorithm fails there is no alternating chain, we introduce a new concept.
A vertex cover in a graph is a set of vertices \(S\) such that every edge in the graph has at least one endpoint in \(S\).
There is always a vertex cover of a graph, namely, the set of all the vertices of the graph. What is clearly more interesting is a smallest vertex cover, which is related to a maximum matching.
If \(M\) is a matching in a graph and \(S\) is a vertex cover, then \(|M|\le |S|\).
- Proof
-
Suppose \(\hat M\) is a matching of maximum size and \(\hat S\) is a vertex cover of minimum size. Since each edge of \(\hat M\) has an endpoint in \(\hat S\), if \(|\hat M|> |\hat S|\) then some vertex in \(\hat S\) is incident with two edges of \(\hat M\), a contradiction. Hence \(|M|\le |\hat M|\le |\hat S|\le |S|\).
Suppose that we have a matching \(M\) and vertex cover \(S\) for a graph, and that \(|M|=|S|\). Then the theorem implies that \(M\) is a maximum matching and \(S\) is a minimum vertex cover. To show that when the algorithm fails there is no alternating chain, it is sufficient to show that there is a vertex cover that is the same size as \(M\). Note that the proof of this theorem relies on the "official'' version of the algorithm, that is, the algorithm continues until no new vertices are labeled.
Suppose the algorithm fails on the bipartite graph \(G\) with matching \(M\). Let \(U\) be the set of labeled \(w_i\), \(L\) the set of unlabeled \(v_i\), and \(S=L\cup U\). Then \(S\) is a vertex cover and \(|M|=|S|\).
- Proof
-
If \(S\) is not a cover, there is an edge \(\{v_i,w_j\}\) with neither \(v_i\) nor \(w_j\) in \(S\), so \(v_i\) is labeled and \(w_j\) is not. If the edge is not in \(M\), then the algorithm would have labeled \(w_j\) at the step after \(v_i\) became labeled, so the edge must be in \(M\). Now \(v_i\) cannot be labeled \((S,0)\), so \(v_i\) became labeled because it is connected to some labeled \(w_k\) by an edge of \(M\). But now the two edges \(\{v_i,w_j\}\) and \(\{v_i,w_k\}\) are in \(M\), a contradiction. So \(S\) is a vertex cover.
We know that \(|M|\le |S|\), so it suffices to show \(|S|\le |M|\), which we can do by finding an injection from \(S\) to \(M\). Suppose that \(w_i\in S\), so \(w_i\) is labeled. Since the algorithm failed, \(w_i\) is incident with an edge \(e\) of \(M\); let \(f(w_i)=e\). If \(v_i\in S\), \(v_i\) is unlabeled; if \(v_i\) were not incident with any edge of \(M\), then \(v_i\) would be labeled \((S,0)\), so \(v_i\) is incident with an edge \(e\) of \(M\); let \(f(v_i)=e\). Since \(G\) is bipartite, it is not possible that \(f(w_i)=f(w_j)\) or \(f(v_i)=f(v_j)\). If \(f(w_i)=f(v_j)\), then \(w_i\) and \(v_j\) are joined by an edge of \(M\), and the algorithm would have labeled \(v_j\). Hence, \(f\) is an injection.
We have now proved this theorem:
In a bipartite graph \(G\), the size of a maximum matching is the same as the size of a minimum vertex cover.
It is clear that the size of a maximum sdr is the same as the size of a maximum matching in the associated bipartite graph \(G\). It is not too difficult to see directly that the size of a minimum vertex cover in \(G\) is the minimum value of \(f(n,i_1,i_2,\ldots,i_k)=n-k+|\bigcup_{j=1}^k A_{i_j}|\). Thus, if the size of a maximum matching is equal to the size of a minimum cover, then the size of a maximum sdr is equal to the minimum value of \(n-k+|\bigcup_{j=1}^k A_{i_j}|\), and conversely. More concisely, Theorem \(\PageIndex{4}\) is true if and only if Theorem 4.3.1 is true.
More generally, in the schematic of Figure \(\PageIndex{6}\), if any three of the relationships are known to be true, so is the fourth. In fact, we have proved all but the bottom equality, so we know it is true as well.
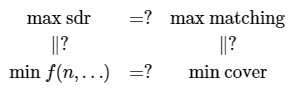
Finally, note that we now have both a more efficient way to compute the size of a maximum sdr and a way to find the actual representatives: convert the sdr problem to the graph problem, find a maximum matching, and interpret the matching as an sdr.


