4.E: Systems of Distinct Representatives (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
4.2: Existence of SDRs
How many different systems of distinct representatives are there for A1={1,2}, A2={2,3}, …, An={n,1}?
How many different systems of distinct representatives are there for the sets Ai=[n]∖i, i=1,2,…,n, n≥2?
Suppose the set system A1,A2,…,An has an sdr, and that x∈Ai. Show the set system has an sdr containing x. Show that x cannot necessarily be chosen to represent Ai.
Suppose the set system A1,A2,…,An satisfies |⋃kj=1Aij|≥k+1 for every 1≤k<n and {i1,i2,…,ik}⊆[n], and that x∈Ai. Show the set system has an sdr in which x represents Ai.
An m×n chessboard, with m even and both m and n at least 2, has one white and one black square removed. Show that the board can be covered by dominoes.
4.3: Partial SDRs
Find the size of a maximum sdr for A1={a,b,c},A2={a,b,c,d,e},A3={a,b},A4={b,c},A5={a},A6={a,c,e}. Justify your answer.
4.4: Latin Squares
Show that there is only one reduced Latin square of order 3.
Verify that the isotopy relation is an equivalence relation.
Find all 4 reduced Latin squares of order 4. Show that there are at most 2 isotopy classes for order 4.
Show that the second set system defined in Example 4.4.5 has an sdr as claimed.
Show that there are no orthogonal Latin squares of order 2.
Find the two orthogonal Latin squares of order 5 as described in Theorem 4.4.1. Show your answer as in Example 4.4.6.
Prove that to construct orthogonal Latin squares of order 2m, m≥2, it suffices to find two orthogonal Latin squares of order 4=22 and two of order 8=23.
An n×n Latin square A is symmetric if it is symmetric around the main diagonal, that is, Ai,j=Aj,i for all i and j. It is easy to find symmetric Latin squares: every addition table modulo n is an example, as in Example 4.4.4. A Latin square is idempotent if every symbol appears on the main diagonal. Show that if A is both symmetric and idempotent, then n is odd. Find a 5×5 symmetric, idempotent Latin square.
The transpose A⊤ of a Latin square A is the reflection of A across the main diagonal, so that A⊤i,j=Aj,i. A Latin square is self-orthogonal if A is orthogonal to A⊤. Show that there is no self-orthogonal Latin square of order 3. Find one of order 4.
4.6: Matchings
In this bipartite graph, find a maximum matching and a minimum vertex cover using the algorithm of this section. Start with the matching shown in red. Copies of this graph are available in this pdf file.
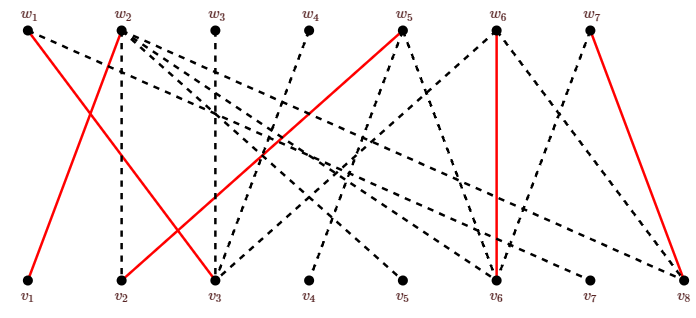
Show directly that that the size of a minimum vertex cover in G is the minimum value of n−k+|⋃kj=1Aij|, as mentioned above.


