10.3: Important Examples
- Page ID
- 83453
the function \(A \to A\) defined by \(a \mapsto a\)
the identity function on on set \(A\)
An identity function is always a bijection.
the function \(A \to X\) defined by \(a \mapsto a\)
the functions \(A \times B \to A\) and \(A \times B \to B\) defined by \((a,b) \mapsto a\) and \((a,b) \mapsto b\)
the projection function onto the first factor \(A\) in the Cartesian product \(A \times B\)
the projection function onto the second factor \(B\) in the Cartesian product \(A \times B\)
Consider \((\dfrac{1}{2},\pi) \in \mathbb{Q} \times \mathbb{R}\text{.}\) Then
\begin{align*} p_{\mathbb{Q}} \left( \dfrac{1}{2}, \pi \right) & = \dfrac{1}{2}, & p_{\mathbb{R}} \left( \dfrac{1}{2}, \pi \right) & = \pi \text{.} \end{align*}
Extend.
We may of course similarly define a projection function on a Cartesian product with any number of factors. Write
to mean the projection function onto the \(i^{th}\) factor \(A_i\) in the Cartesian product
Alternatively, we may write
for this function.
A projection is always surjective (except possibly when one or more of the factors in the Cartesian product is the empty set).
the “induced” function \(A \to Y\) created from function \(f: X\rightarrow Y\) and subset \(A \subseteq X\) by “forgetting” about all elements of \(X\) that do not lie in \(A\)
restriction of function \(f: X\rightarrow Y\) to subset \(A \subseteq X\)
alternative domain restriction notation
alternative domain restriction notation
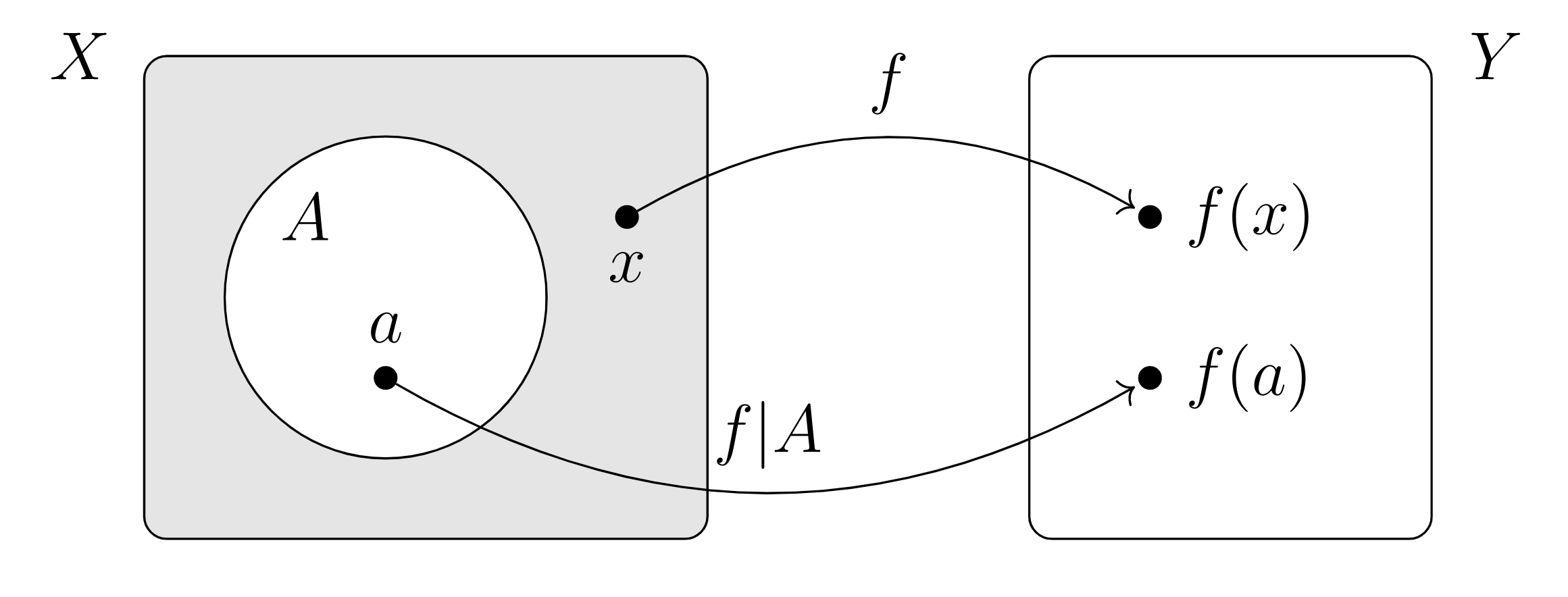
For \(f: \mathbb{Z} \rightarrow \mathbb{N}\text{,}\) \(f(m) = \vert m \vert \text{,}\) we have \(f \vert _{\mathbb{N}} = \id_{\mathbb{N}}\text{.}\)
Consider function \(f: X\rightarrow Y\) and subset \(A \subseteq X\text{.}\)
- If \(f\) is injective, is \(f \vert _A\) injective?
- If \(f \vert _A\) is injective, must \(f\) be injective?
- Answer the previous two questions replacing “injective” with “surjective”.
The concept of restricting the domain makes our previously defined concept image of a function on a subset unnecessary: for function \(f: X\rightarrow Y\) and subset \(A \subseteq X\text{,}\) the image of \(f\) on \(A\) is the same as the image of the restriction \(f \vert _A\text{.}\)
the “induced” function \(X \to B\) created from function \(f: X\rightarrow Y\) and subset \(B \subseteq Y\) by “forgetting” about all elements of \(Y\) that do not lie in \(B\text{,}\) where \(B\) must contain the image of \(f\)
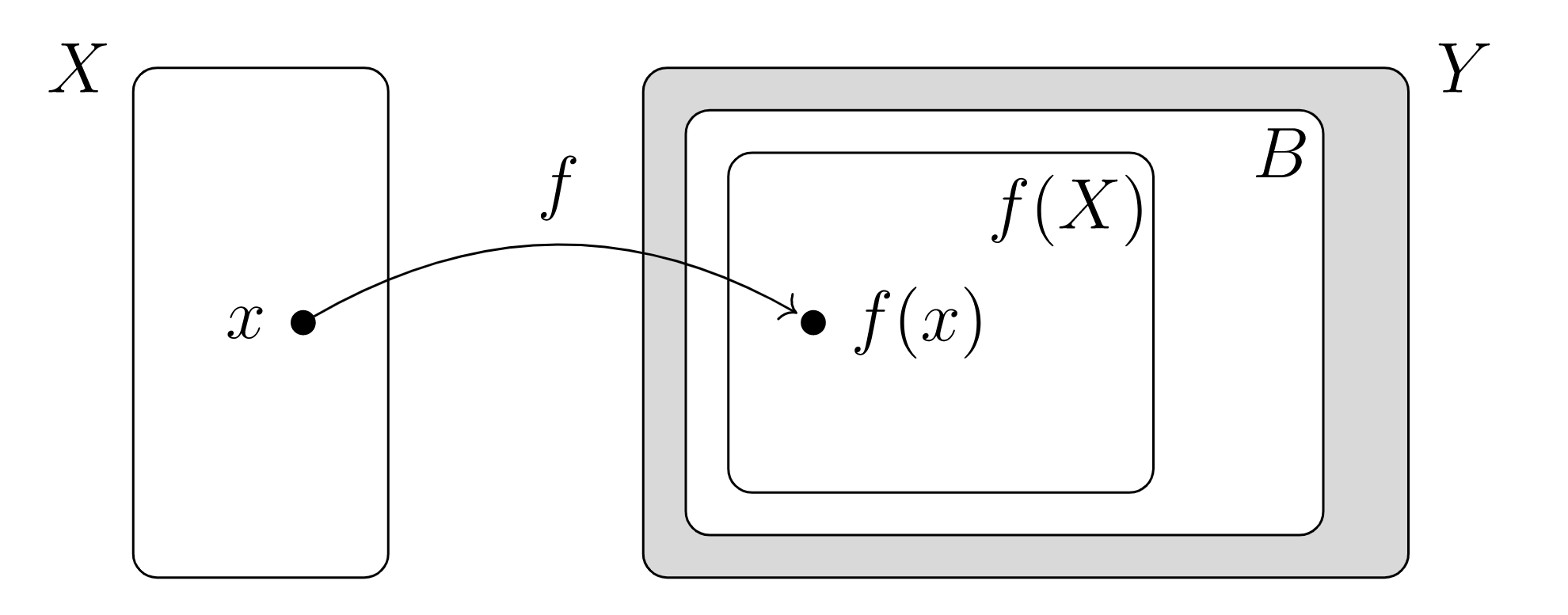
Consider \(f: \mathbb{R} \rightarrow \mathbb{R}\text{,}\) \(f(x) = x^2\text{.}\) It would be more precise to write \(f: \mathbb{R} \rightarrow \mathbb{R}_{\geq 0} \\text{,}\) since \(x^2 \ge 0\) for all \(x \in \mathbb{R}\text{.}\)
If we restrict the codomain all the way down to the image set \(f(X)\text{,}\) the resulting map \(f : X \rightarrow f(X) \) is always surjective. In particular, if \(f: X \xrightarrow Y\) is injective, then by restricting the codomain we can obtain a bijection \(f : X \rightarrow f(X) \text{.}\)
relative to function \(f: A \rightarrow B\) and superset \(X \supseteq A\text{,}\) a function \(g: X \rightarrow B\) so that \(g(a) = f(a)\) for all \(a \in A\)
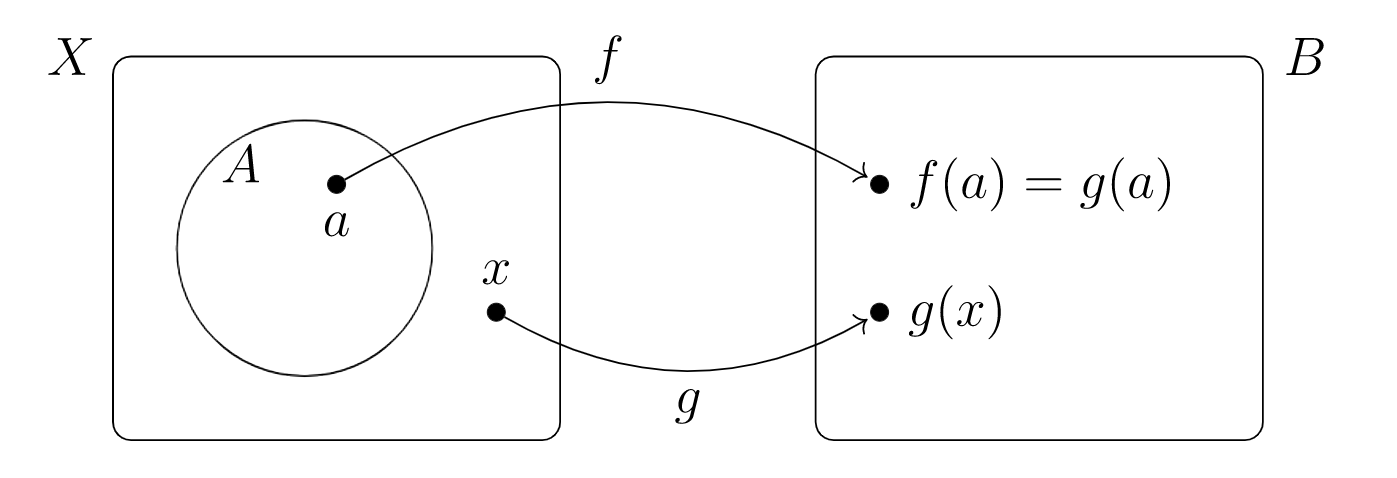
The condition defining the concept extension function can be more succinctly stated as requiring function \(g: X \rightarrow B\) with \(A \subseteq X\) satisfy \(g \vert _A = f\text{.}\)
Write \(\text{flr}:\mathbb{R} \rightarrow \mathbb{Z}\) to mean the floor function: for real input \(x\text{,}\) the output \(\text{flr} (x)\) is defined to be the greatest integer that is less than or equal to \(x\text{.}\) Usually we write
\begin{equation*} \text{flr} (x) = \lfloor x \rfloor \text{.} \end{equation*}
As every integer is less than or equal to itself, we have \(\text{flr} (z) = z\) for every \(z \in \mathbb{Z}\text{.}\) This says that the floor function is an extension of the identity function \(\id_{\mathbb{Z}}\text{.}\)
One of the most common ways to extend a function to a larger domain is to pick an appropriate constant value in the codomain to assign to all “new” inputs in the enlarged domain.
relative to function \(f: A \rightarrow Z\) and superset \(X \supseteq A\text{,}\) where \(Z\) is a set of “numbers” containing a zero element, the extension function \(g: X \rightarrow Z\) defined by
\begin{equation*} g(x) = \begin{cases} f(x)\text{,} & x \in X \text{,} \\ 0\text{,} & \text{otherwise.} \end{cases} \end{equation*}
Define \(\widetilde{\id}_{\mathbb{Z}} : \mathbb{R} \rightarrow \mathbb{Z}\) by
\begin{equation*} {\widetilde{\id}}_{\mathbb{Z}}(x) = \begin{cases} x\text{,} & x \in \mathbb{Z} \text{,} \\ 0\text{,} & \text{otherwise.} \end{cases} \end{equation*}
Then \(\widetilde{\id}_{\mathbb{Z}}\) is the extension by zero of the identity function \(\id_{\mathbb{Z}}\text{.}\)
- Compare.
-
Example \(\PageIndex{4}\) also involved an extension of the identity function \(\id_{\mathbb{Z}}\) — was it an extension by zero?


