15.3: Connected Vertices, Graphs, and Components
- Page ID
- 83480
a pair of vertices \(v,v'\) such that there exists a walk beginning at \(v\) and ending at \(v'\)
every pair of vertices is connected
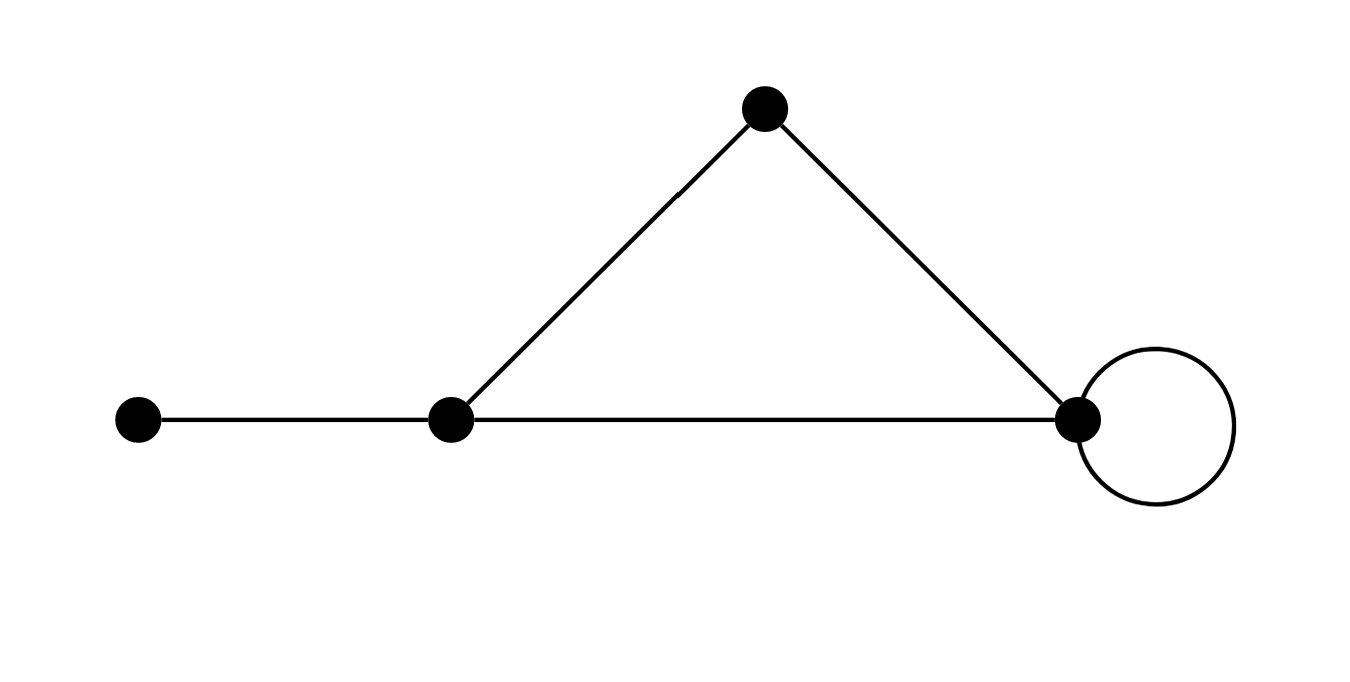
Being connected is a symmetric relationship between vertices, and walks connecting vertices can be shortened to paths.
Assume \(v,v'\) are vertices in a graph. Then the following are equivalent.
- Vertices \(v,v'\) are connected.
- There exists a walk beginning at \(v\) and ending at \(v'\text{.}\)
- There exists a path beginning at \(v\) and ending at \(v'\text{.}\)
- There exists a walk beginning at \(v'\) and ending at \(v\text{.}\)
- There exists a path beginning at \(v'\) and ending at \(v\text{.}\)
- Proof Idea.
-
As usual, we prove the equivalence of multiple statements using a cycle of logical implications.
Statement 1 implies Statement 2.
This is the definition of connected vertices.Statement 2 implies Statement 3.
Suppose \(v_0, e_1, v_1, \ldots, v_{n - 1}, e_n, v_n\) is a walk with \(v_0 = v\) and \(v_n = v'\text{.}\) If this walk is not a path, then there is a repeated vertex. Suppose \(v_j = v_i\) with \(j \gt i\text{.}\) Then\begin{equation*} v_0, e_1, v_1, \ldots, v_{i-1}, e_i, v_j, e_{j+1}, \ldots, v_{n - 1}, e_n, v_n \end{equation*}
is also a walk from \(v\) to \(v'\text{.}\) Keep removing repeated vertices in this way until a path is obtained.Statement 3 implies Statement 4.
Just reverse the order of the vertices and edges in the path from \(v\) to \(v'\) to obtain a walk in the other direction.Statement 4 implies Statement 5.
As before, if the walk from \(v'\) to \(v\) is not a path, each pair of repeated vertices can be eliminated by “snipping out” the portion of the walk between them.Statement 5 implies Statement 1.
Reverse the path from \(v'\) to \(v\) to obtain a walk from \(v\) to \(v'\text{,}\) thereby satisfying the definition of connected vertices.
A nonconnected graph can be considered to simply be a collection of connected subgraphs.
a connected subgraph of a graph which is not contained in any larger connected subgraph of that graph
a subgraph \(G'\) of a graph \(G\) that satisfies the following:
- \(G'\) is connected;
- if \(G''\) is a subgraph of \(G\) such that \(G''\) is connected and \(G' \preceq G''\text{,}\) then \(G'' = G'\)
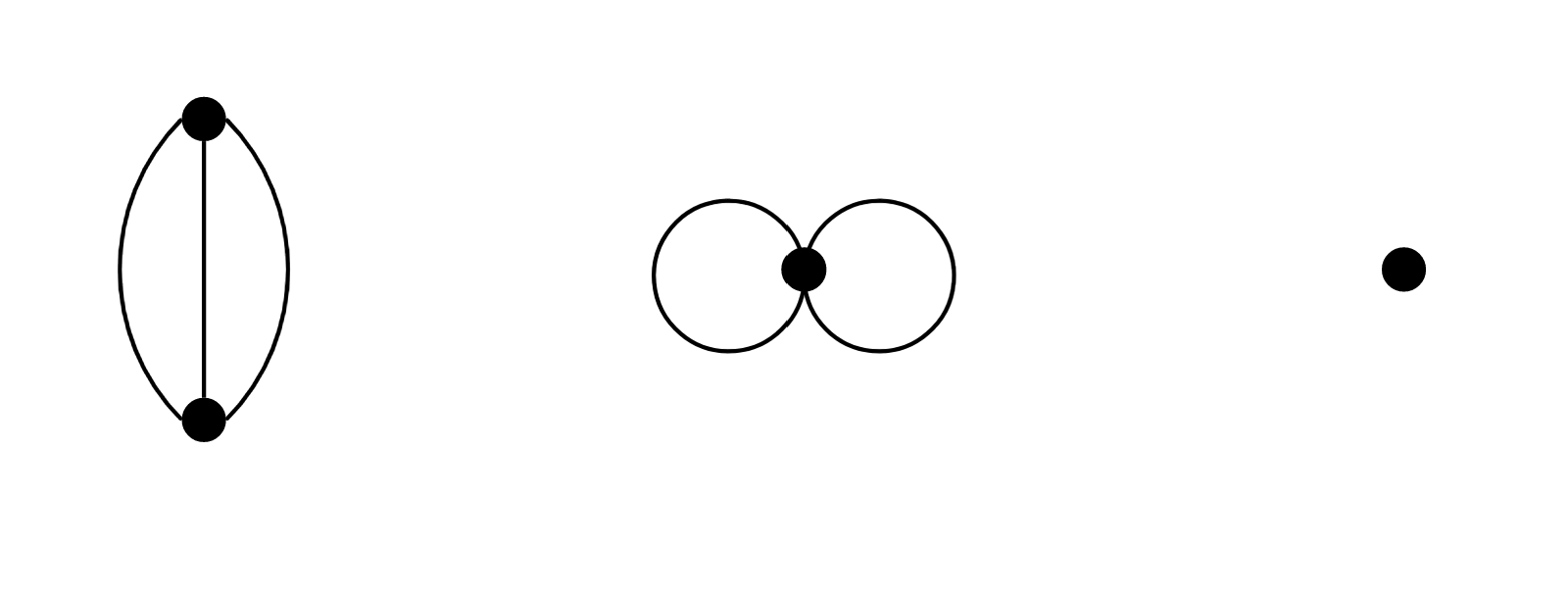
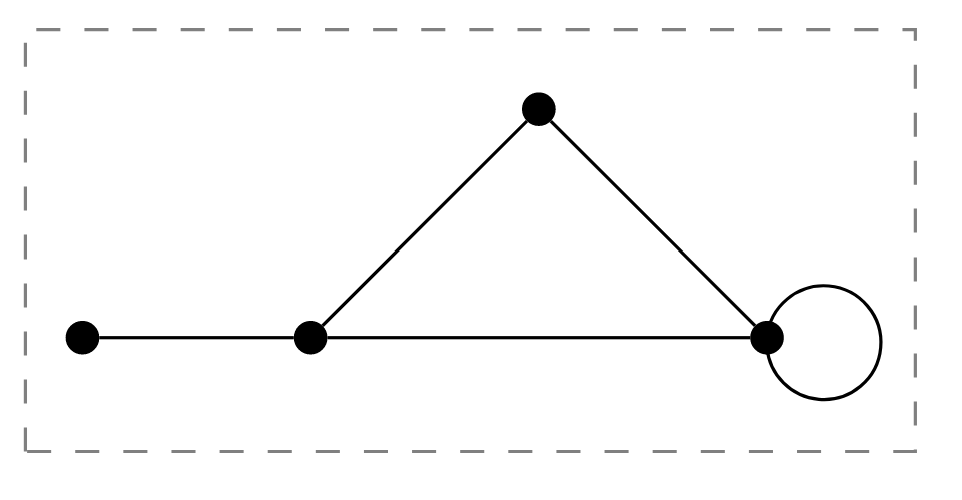
Considering Figure \(\PageIndex{3}\) below as a single graph, we have placed the connected components (of which there are three) into boxes.
This nonconnected graph has other connected subgraphs. For example, the subgraph that contains only the left-most two vertices joined by a single edge is a connected subgraph. But that connected graph is not a connected component because it is a subgraph of a larger connected subgraph.
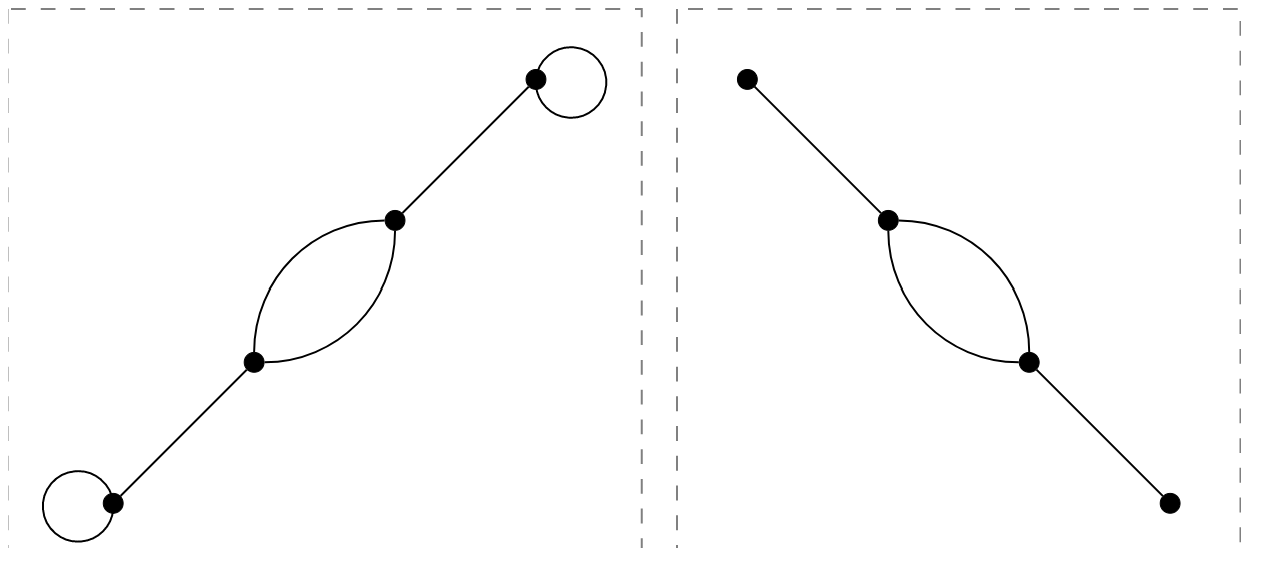
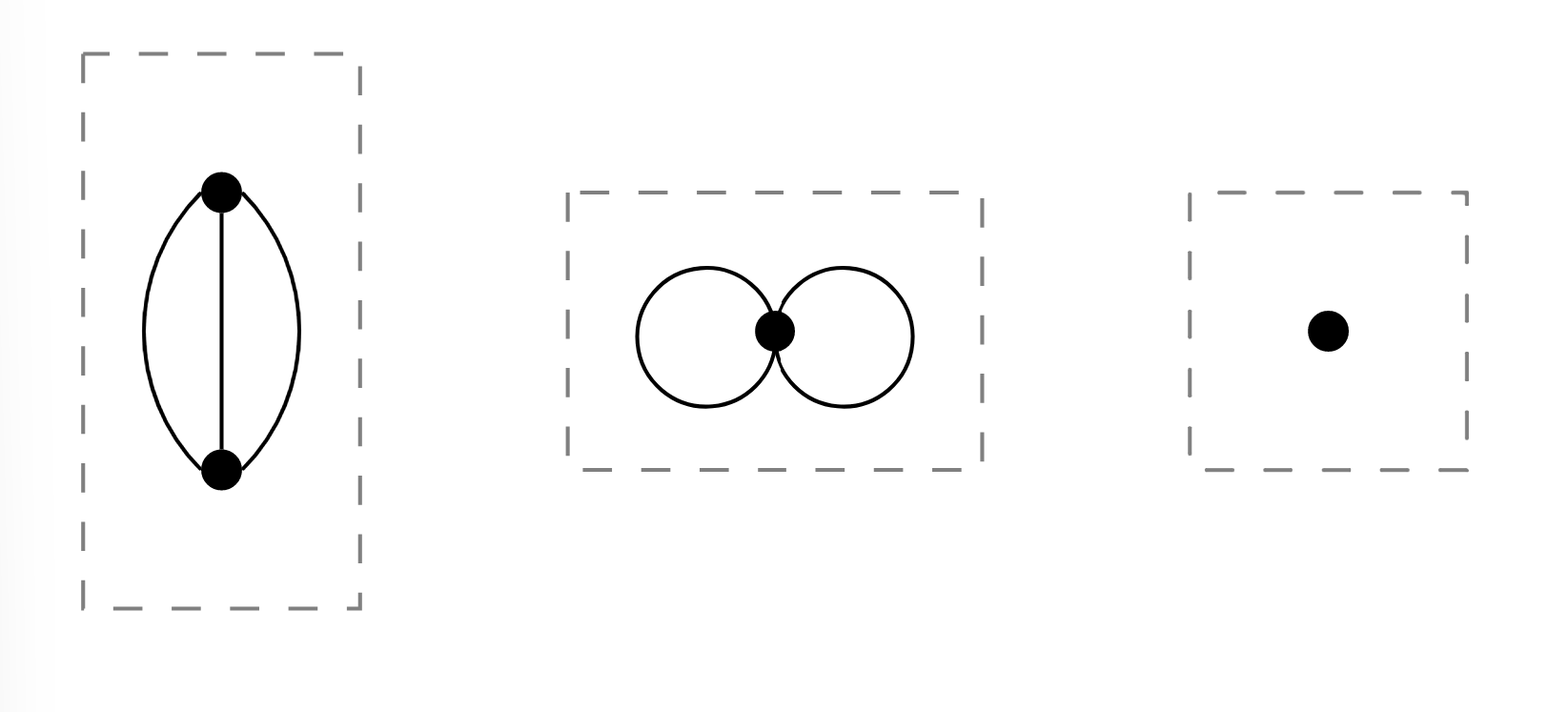
The two graphs in Figure \(\PageIndex{4}\) are in fact the same graph, just with different diagrammatic representations. In the second version of the graph, we have again identified connected components by placing each of them in a box.
If a graph is connected, then the entire graph is a largest connected subgraph possible.
As in our working definition, informally the connected components of a graph \(G\) are the “largest” subgraphs of \(G\) that are connected. The second condition in the formal definition is just a positive way of stating the working definition. We will make the general notion of “largest” more precise in a similar way in Chapter 19 (see the definition of maximal element, the Test for Maximal/Minimal Elements, as well as Example 19.5.3).
If \(G = (V,E)\) is connected and \( \vert V \vert = n\text{,}\) then \(\vert E \vert \ge n - 1\text{.}\)
- Proof
-
By (strong) induction.
Base case \(n=1\).
Every graph with only one vertex is connected and satisfies \(\vert E \vert \ge 0\text{.}\)Induction step.
Assume \(k \ge 1\) and the statement is true for all \(n \le k\text{.}\) Let \(G = (V,E)\) be a connected graph with \(k + 1\) vertices. We must show \(\vert E \vert \ge k\text{.}\)Arbitrarily choose some vertex \(v_0 \in V\text{,}\) and let \(G' = (V', E')\) be the graph obtained from \(G\) by removing \(v_0\) and all edges incident to it. Unfortunately, \(G'\) might not be connected. Let \(G_1', \ldots, G_\mathscr{l}'\) be its connected components. Write \(G_i' = (V_i',E_i')\text{,}\) and let \(n_i = \vert V_i' \vert\text{.}\) Then each \(G_i'\) is connected and has at most \(k\) vertices, so the induction hypothesis applies. Also note that \(n_1 + \cdots + n_\mathscr{l} = k\text{,}\) since every vertex of \(G\) except \(v_0\) is part of exactly one subgraph \(G_i'\text{.}\)
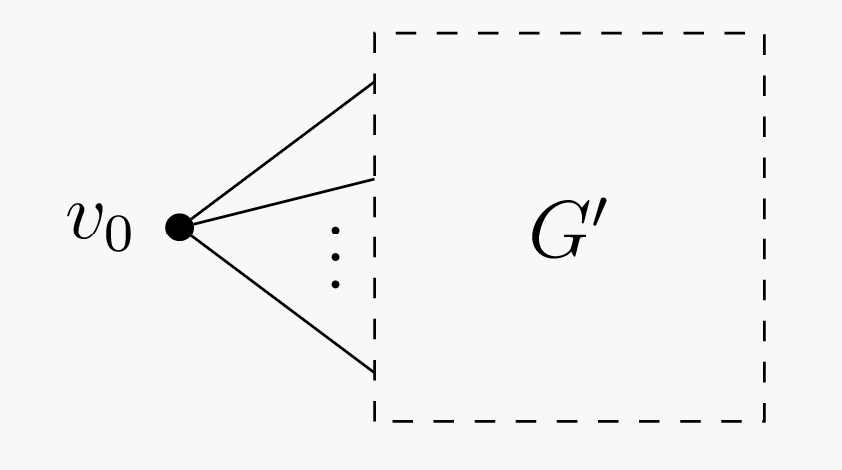
(a) “Extra” vertex \(v_0\) and the remaining subgraph \(G'\text{.}\)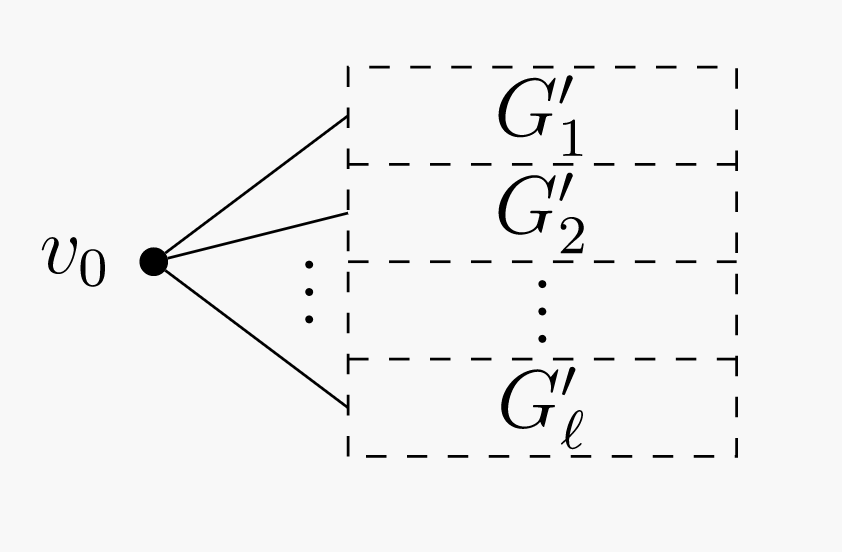 
(b) Subgraph \(G'\) split into connected components.Figure \(\PageIndex{6}\): Removing “extra” vertex \(v_0\text{,}\) splitting remaining subgraph into connected components. Therefore, using our induction hypothesis we may calculate
\begin{align*} \vert E \vert & = \vert E' \vert + \vert \{\text{edges in } G \text{ incident to } v_0\} \vert \\ & = \vert E_1' \vert + \cdots \vert E_\mathscr{l}' \vert + \vert \{\text{edges in } G \text{ incident to } v_0\} \vert \\ & \ge (n_1 - 1) + \cdots + (n_\mathscr{l} - 1) + \vert \{\text{edges in } G \text{ incident to } v_0\} \vert \\ & = k - \mathscr{l} + \vert \{\text{edges in } G \text{ incident to } v_0\} \vert . \end{align*}
However, since \(G\) is connected, \(v_0\) must be the glue keeping the subgraphs \(\{G_i'\}\) together. That is, for each \(i\) there must be at least one edge between \(v_0\) and some vertex of \(G_i'\text{.}\) Therefore,\begin{align*} \vert E \vert & \ge k - \mathscr{l} + \vert \{\text{edges in } G \text{ incident to } v_0\} \vert \\ & \ge k - \mathscr{l} + \mathscr{l} \\ & = k. \end{align*}