19.5: Maximal/minimal Elements

Each of the following definitions are for a subset \(B\) of a partially ordered set \(A\text{.}\)

Definition: Upper bound

an element \(u \in A\) such that \(b \preceq u\) for all \(b \in B\)

Definition: Least upper bound

an upper bound for \(B \subseteq A\) that is less than every other upper bound

Definition: Maximum element

an upper bound for \(B\) that is contained in \(B\)

Definition: Lower bound

an element \(\ell \in A\) such that \(\ell \preceq b\) for all \(b \in B\)

Definition: Greatest lower bound

a lower bound for \(B \subseteq A\) that is greater than every other lower bound

Definition: Minimum element

a lower bound for \(B\) that is contained in \(B\)

Warning \(\PageIndex{1}\)

1. An upper or lower bound does not need to belong to the subset for which it is a bound.
2. A set (or subset) does not necessarily have either a maximum or minimum element.

Fact \(\PageIndex{1}\)

If a subset of a partially ordered set contains a maximum element, then that maximum element is unique. And similarly for a minimum element.

Proof.

You are asked to prove this in Activity 19.7.5.

Example \(\PageIndex{1}\): Maximums, minimums, and bounds in \(\mathbb{R}\).

Consider the usual (total) order \(\mathord{\leq}\) on \(\mathbb{R}\text{.}\)

• The full set \(\mathbb{R}\) has neither a maximum nor minimum element.
• The subset \((0,1)\) has many upper bounds (anything \(\geq 1\)) and many lower bounds (anything \(\leq 0\)). However, we would refer to \(1\) as the least upper bound and to \(0\) as the greatest lower bound of \((0,1)\text{.}\)
• The subset \((0,1)\) has no maximum or minimum element. However, the subset \([0,1]\) has maximum \(1\) and minimum \(0\text{.}\)

Example \(\PageIndex{2}\): Maximums, minimums, and bounds in a power set.

Suppose \(U\) is a universal set, and consider \(\mathscr{P}(U)\) partially ordered by \(\mathord{\subseteq}\) as usual. In the full set \(\mathscr{P}(U)\text{,}\) the unique maximum element is \(U\text{,}\) which is just another way of saying that every element of \(\mathscr{P}(U)\) is a subset of \(U\text{.}\) And the unique minimum element is \(\emptyset\text{,}\) which is just another way of saying that the empty set is a subset of every subset of \(U\text{.}\)

Now consider a subset \(\mathscr{A} \subseteq \mathscr{P}(U)\text{,}\) so that \(\mathscr{A}\) is a collection of subsets of \(U\text{.}\) Because of the existence of maximum and minimum elements, these elements also serve as an upper and lower bound, respectively, for \(\mathscr{A}\text{.}\) However, one can also find a least upper bound for \(\mathscr{A}\) by taking the union of all the subsets of \(U\) contained in \(\mathscr{A}\text{,}\) and one can find a greatest lower bound by taking the intersection of all the subsets of \(U\) contained in \(\mathscr{A}\text{.}\)

The next two definitions are stated for elements in a partially ordered set, but could also be understood for elements in a subset of a partially ordered set, as every subset of a partially ordered set is also a partially ordered set.

Definition: Maximal Element

an element for which no other element is larger

Definition: Minimal Element

an element for which no other element is smaller

Remark \(\PageIndex{1}\)

The difference between maximum and maximal is subtle. A maximum element must be larger than (and hence comparable to) every other element of \(A\text{,}\) while a maximal element must only be larger than every other element of \(A\) to which it is comparable. The distinction between minimum and minimal is similar.

Test \(\PageIndex{1}\): Maximal/minimal elements.

1. To verify that \(\overline{m} \in A\) is maximal, prove either the original definition

\begin{equation*} (\forall x \in A)({x \neq \overline{m}} \Rightarrow {\overline{m} \npreceq x}) \text{,} \end{equation*}
or prove the equivalent contrapositive formulation
\begin{equation*} (\forall x \in A)({\overline{m} \preceq x} \Rightarrow {x = \overline{m}}) \text{.} \end{equation*}

 

2. To verify that \(\underline{m} \in A\) is minimal, prove either the original definition

\begin{equation*} (\forall x \in A)({x \neq \underline{m}} \Rightarrow {x \npreceq \underline{m}}) \text{,} \end{equation*}
or prove the equivalent contrapositive formulation
\begin{equation*} (\forall x \in A)({x \preceq \underline{m}} \Rightarrow {x = \underline{m}}) \text{.} \end{equation*}
 

Example \(\PageIndex{3}\): Connected components are maximal.

Consider the graph \(G\) in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): An example non-connected graph.

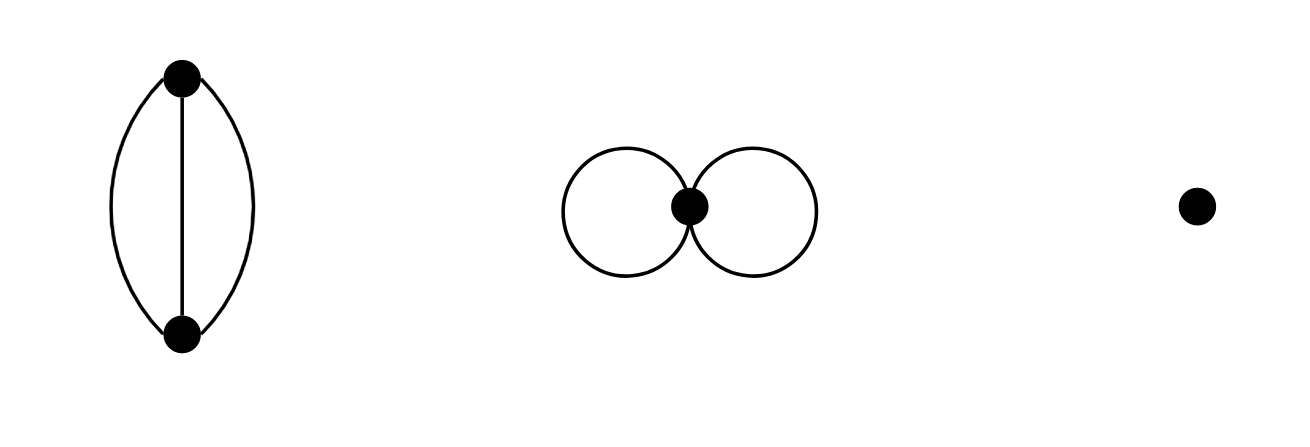
Let \(S(G)\) represent the collection of subgraphs of \(G\text{,}\) partially ordered by the subgraph relation. (By my count, \(\vert S(G) \vert = 110\text{.}\)) Let \(C(G)\) represent the collection of connected subgraphs of \(G\text{.}\) (By my count, \(\vert C(G) \vert = 15\text{.}\)) A maximal elements of \(C(G)\) would have to be a connected subgraph of \(G\) that is contained in no larger connected subgraph of \(G\) — but this is precisely the definition of connected component. Hence \(C(G)\) has three maximal elements, the three connected components you see in Figure \(\PageIndex{1}\). However, a maximum element of \(C(G)\) would be a connected subgraph of \(G\) which contains every other connected subgraph of \(G\text{,}\) and the existence of multiple connected components in this example non-connected graph makes such a subgraph impossible.

Remark \(\PageIndex{2}\)

If you compare both our informal definition and formal definition of connected component with our definition of maximal element and our Test for Maximal/Minimal Elements, you should find that the definition of connected component means precisely a maximal subgraph with respect to the property of being connected.

Example \(\PageIndex{4}\)

Let \(A = \{a,b,c\}\text{.}\) Given the Hasse diagram for \(\mathord{\subseteq}\) on \(P = \mathscr{P}(A)\setminus\{A\}\) in Figure \(\PageIndex{2}\), determine all maximal/maximum/minimal/minimum elements, if they exist.

Figure \(\PageIndex{2}\): The Hasse Diagram for \(\subseteq\) on an "uncapped" power set

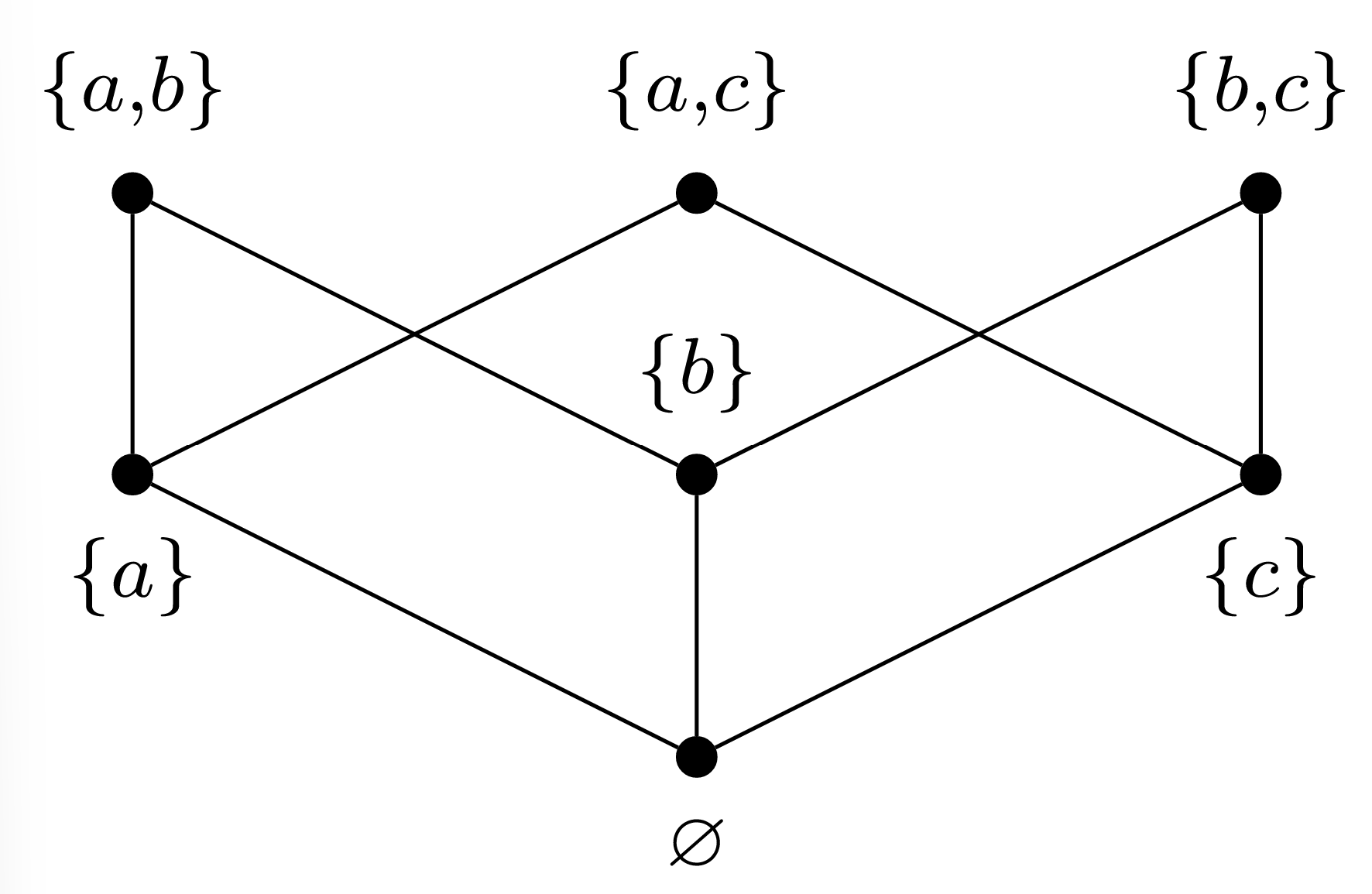
Solution

The element \(\{a,b\}\) is maximal, since each node in the Hasse diagram that is adjacent to \(\{a,b\}\) is below it. The same reasoning confirms that \(\{a,c\}\text{,}\) and \(\{b,c\}\) of are also maximal. However, none of them is a maximum, since none of them is larger than the other two.

The element \(\emptyset\) of \(P\) is a minimal element, since each node that is adjacent to it is above it. And it is the only minimal element. Furthermore, \(\emptyset\) is the minimum element, since for every other node there is a walk upwards from \(\emptyset\) to that node.

Warning \(\PageIndex{2}\)

Just drawing a node higher or lower in a Hasse diagram does not necessarily make it larger or smaller, respectively, when compared to other elements via the partial order. For example, in the Hasse diagram of Figure \(\PageIndex{2}\), we could have drawn the node for \(\{a,c\}\) at a higher location, but that would not make it larger than \(\{a,b\}\) and \(\{b,c\}\text{,}\) since there still would not have been any edges or chains of edges from \(\{a,c\}\) downward to those other two nodes.

Fact \(\PageIndex{2}\)

If the partially ordered set \(A\) has a maximum element, then that element is also the only maximal element of \(A\text{.}\) Similarly, the minimum element, if it exists, is the only minimal element of \(A\text{.}\)

Proof Idea.

Assume \(A\) has a maximum element. Then every element of \(A\) is both comparable to and smaller than that maximum element, so no element is larger than it. Therefore, this maximum must be maximal. And no other element could be maximal, because to be maximal means there are no elements which are larger. But our maximum element is always larger.

Warning \(\PageIndex{3}\)

A maximum element must be maximal and must be the only maximal. But a maximal element, even if it is the only one, need not be the maximum.

Example \(\PageIndex{5}\): A partially ordered set with exactly one maximal element but no maximum element

Consider

\begin{equation*} A = \{3\} \cup \{2,4,8,16,32,64,\ldots,2^n,\ldots\}, \end{equation*}
partially ordered by \(\mathord{\mid}\text{,}\) the “divides” relation. There is no element of \(A\) that is divisible by \(3\) (except \(3\) itself), so there is no element of \(A\) that is larger than \(3\text{.}\) Therefore, \(3\) is maximal. Moreover, \(3\) is the only maximal element in \(A\text{,}\) since every power of \(2\) divides the next power of \(2\text{.}\) However, there is no maximum element in \(A\text{,}\) since there is no element of \(A\) which is divisible by every other element of \(A\text{.}\)

Example \(\PageIndex{6}\): A partially ordered set with infinitely many maximal/minimal elements but no maximum/minimum element.

Consider \(\mathscr{A} \subsetneqq \mathscr{P}(\mathbb{N})\text{,}\) where

\begin{equation*} \mathscr{A} = \mathscr{P}(\mathbb{N}) \setminus \{\emptyset,\mathbb{N}\} \text{.} \end{equation*}
So \(\mathscr{A}\) is the set of all nonempty, proper subsets of \(\mathbb{N}\text{.}\) Under the partial order \(\mathord{\subseteq}\text{,}\) \(\mathscr{A}\) has neither a maximum nor a minimum element, but for every \(n \in \mathbb{N}\text{,}\) \(\{n\}\) is a minimal element and \(\mathbb{N} \setminus \{n\}\) is a maximal element of \(\mathscr{A}\text{.}\)