19.4: Total Orders
- Page ID
- 83502
Definition: Comparable Elements
elements \(a,b\) in a partially ordered set such that either \(a \preceq b\) or \(b \preceq a\)
Definition: Incomparable Elements
elements that are not comparable
Example \(\PageIndex{1}\): Comparable and incomparable subsets.
Let \(U\) represent some universal set containing at least two elements, and consider \(\mathscr{P}(U)\) partially ordered by \(\mathord{\subseteq}\text{.}\)
- Both the empty set \(\emptyset\) and the universal set \(U\) are comparable to every element of \(\mathscr{P}(U)\text{.}\)
- For \(x,y\in U\) with \(x\ne y\text{,}\) then \(\{x\},\{y\}\) are incomparable.
- In fact, for every non-empty, proper subset \(A \subsetneqq U\) there exists a subset \(B \subseteq U\) which is incomparable to \(A\text{:}\) take \(B = A^C\text{.}\)
However, do not let the second two points above lead you astray: it is not necessary for subsets to be disjoint in order to be incomparable. As long as each of a pair of subsets contains an element that the other doesn't, then the two will be incomparable by \(\mathord{\subseteq}\text{.}\)
Definition: Total Order
a partial order on a set such that every pair of elements is comparable
Definition: Totally Ordered Set
a set equipped with a total order
Example \(\PageIndex{2}\): Subset order is not total.
For universal set \(U\text{,}\) order \(\mathord{\subseteq}\) on \(\mathscr{P}(U)\) is not total except when \(\vert U \vert \le 1\text{.}\)
Example \(\PageIndex{3}\): Usual order of numbers is total.
Our usual order for numbers, \(\mathord{\leq}\text{,}\) is a total order on \(\mathbb{N}\text{,}\) on \(\mathbb{Z}\text{,}\) on \(\mathbb{Q}\text{,}\) or on \(\mathbb{R}\text{.}\)
Example \(\PageIndex{4}\): Total order on alphabet induces total order on words.
If \(\mathord{\preceq}\) is a total order on an alphabet \(\Sigma\text{,}\) then the lexicographic order \(\preceq^\ast\) described in Example 19.2.6 is a total order on the set of words \(\Sigma^{\ast}\text{.}\)
Example \(\PageIndex{5}\): Pulling back a total order through an injection.
If \(B\) is totally ordered and we use an injection \(f: A \hookrightarrow B\) to “pull back” the order on \(B\) to an order on \(A\) (see Example 19.2.10), then the newly created order on \(A\) will also be total.
Example \(\PageIndex{6}\): Countable can be totally ordered.
If \(A\) is a countably infinite set, then there exists a bijection \(f: \mathbb{N} \rightarrow A\text{.}\) We can use the inverse \(f^{-1}: A \rightarrow \mathbb{N}\) to “pull back” the usual total order \(\mathord{\le}\) on \(\mathbb{N}\) to a total order on \(A\) (see Example \(\PageIndex{5}\)).
Another point of view on this is that our bijection \(f\) creates an infinite sequence
\begin{equation*} a_0, a_1, a_2, \ldots \text{,} \end{equation*}
where each element of \(A\) appears exactly once. This sequence can be turned into a specification of the total order on \(A\) by just turning the commas into \(\mathord{\le}\) symbols:
\begin{equation*} a_0 \le a_1 \le a_2 \le \cdots \text{.} \end{equation*}
The pattern of Example \(\PageIndex{6}\) becomes even simpler when we apply it to a finite set: a total order on a finite set is no different than an ordering of the set elements into a list, as
\begin{equation*} a_0, a_1, a_2, \ldots, a_n \end{equation*}
can simply be turned into
\begin{equation*} a_0 \le a_1 \le a_2 \le \cdots \le a_n \text{,} \end{equation*}
and vice versa.
If \(A\) is a finite, totally ordered set, what does the corresponding Hasse diagram look like?
The answer to this question is contained in Remark \(\PageIndex{1}\).
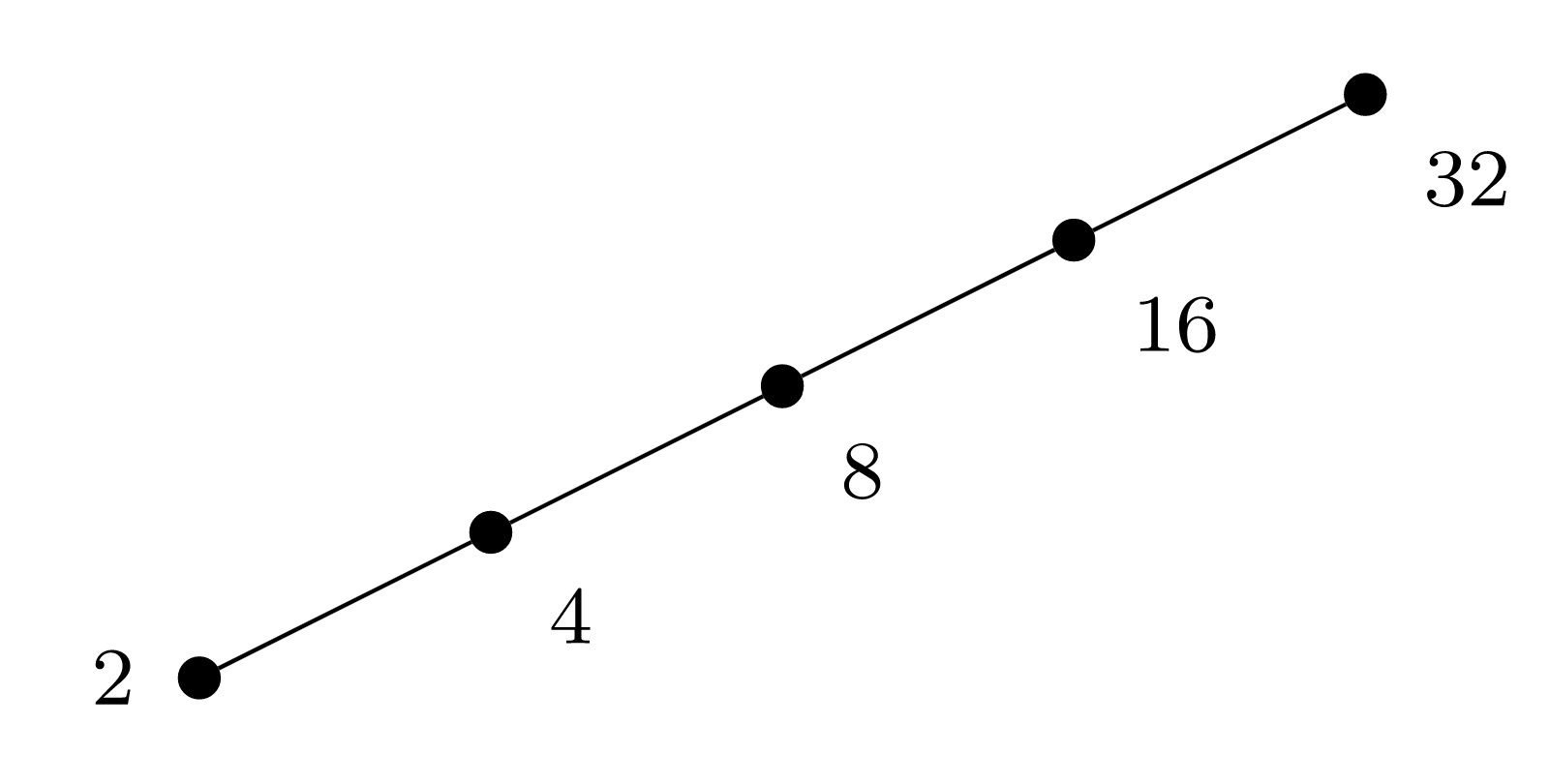
A partial order on a finite set is total if and only if its Hasse diagram forms a single vertical line.
Example \(\PageIndex{7}\): A totally ordered finite set.
Figure \(\PageIndex{1}\) exhibits the Hasse diagram for the total order \(\mathord{\mid}\) on the set \(\{2,4,8,16,32\}\text{,}\) though we have drawn the diagram on a slant from the vertical to be make it easier to see the entire diagram at a glance.