18.7: Exercises

Last updated
Save as PDF

Page ID: 93871

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Exercise \(\PageIndex{1}\)

Let \(\mathord{\equiv}\) represent the relation on \(\mathbb{R}\times\mathbb{R}\) where \((x_1,y_1) \equiv (x_2,y_2)\) means \(y_1 - x_1^2 = y_2 - x_2^2\text{.}\)

Verify that \(\mathord{\equiv}\) is an equivalence relation.
Describe the equivalence classes \([(0,0)]\text{,}\) \([(0,1)]\text{,}\) and \([(1,0)]\) geometrically as sets of points in the plane.

Exercise \(\PageIndex{2}\)

Given a connected (undirected) graph \(G\text{,}\) we can define a relation on the set \(V\) of vertices in \(G\) as follows: let \(v_1 R v_2\) mean that there exists a trail within \(G\) beginning at vertex \(v_1\) and ending at vertex \(v_2\) that traverses an even number of edges.

Prove that \(R\) is an equivalence relation on \(V\text{.}\)
Determine the equivalence classes for this relation when \(G\) is the graph below.

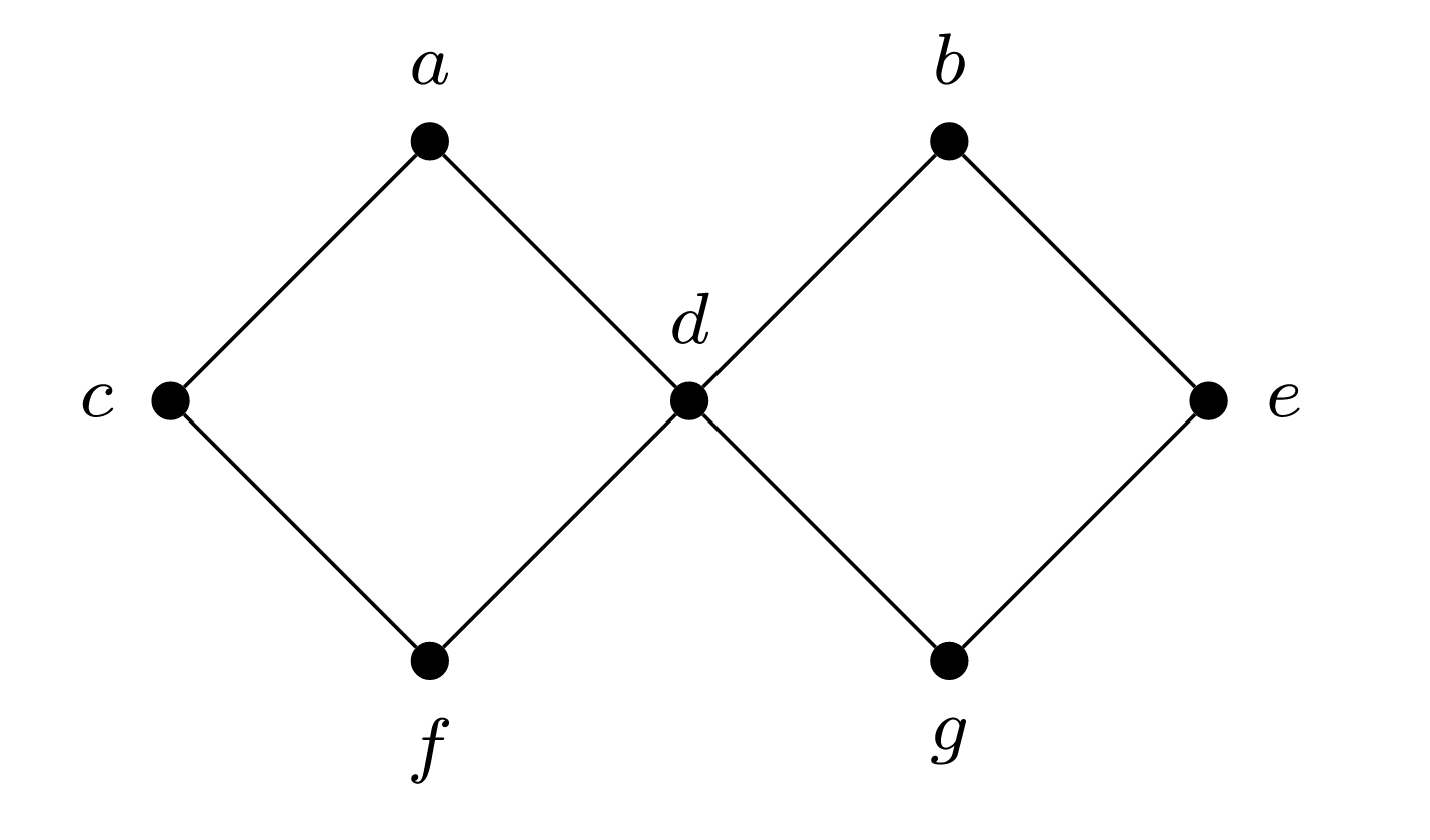
Equivalence relations and classes.

In each of Exercises 3–12, you are given a set \(A\) and a relation \(R\) on \(A\text{.}\) Determine whether \(R\) is an equivalence relation, and, if it is, describe its equivalence classes. Try to be more descriptive than just “\([a]\) is the set of all elements that are equivalent to \(a\text{.}\)”

Exercise \(\PageIndex{3}\)

\(A = \{a, b, c\} \text{;}\) \(R = \{(a,a),(b,b),(c,c),(a,b),(b,a)\} \text{.}\)

Exercise \(\PageIndex{4}\)

\(A = \{-1, 0, 1\} \text{;}\) \(R = \{(x,y) | x^2 = y^2\} \text{.}\)

Exercise \(\PageIndex{5}\)

\(A\) is the power set of some set; \(R\) is the subset relation.

Exercise \(\PageIndex{6}\)

\(A = \mathbb{R} \text{;}\) \(x_1 \mathrel{R} x_2 \) means \(f(x_1) = f(x_2) \text{,}\) where \(f: \mathbb{R} \rightarrow \mathbb{R}\) is the function \(f(x) = x^2 \text{.}\)

Exercise \(\PageIndex{7}\)

\(A\) is some abstract set; \(a_1 \mathrel{R} a_2\) means \(f(a_1) = f(a_2)\text{,}\) where \(f: A \rightarrow B\) is an arbitrary function with domain \(A\text{.}\)

Exercise \(\PageIndex{8}\)

\(A\) is the set of all “formal” expressions \(a/b\text{,}\) where \(a,b\) are integers and \(b\) is nonzero; \((a/b) \mathrel{R} (c/d) \) means \(ad = bc \text{.}\)

Note: Do not think of \(a/b\) as a fraction in the usual way; instead think of it as a collection of symbols consisting of two integers in a specific order with a forward slash between them.

Exercise \(\PageIndex{9}\)

\(A\) is the power set of some finite set; \(X \mathrel{R} Y\) means \(\vert X \vert = \vert Y \vert \text{.}\)

Exercise \(\PageIndex{10}\)

\(A\) is the set of all straight lines in the plane; \(L_1 \mathrel{R} L_2\) means \(L_1\) is parallel to \(L_2\text{.}\)

Exercise \(\PageIndex{11}\)

\(A\) is the set of all straight lines in the plane; \(L_1 \mathrel{R} L_2\) means \(L_1\) is perpendicular to \(L_2\text{.}\)

Exercise \(\PageIndex{12}\)

\(A = \mathbb{R} \times \mathbb{R} \text{;}\) \((x_1,y_1) \mathrel{R} (x_2,y_2)\) means \(x_1^2 + y_1^2 = x_2^2 + y_2^2 \text{.}\)

Hint.: Does the expression \(x^2 + y^2\) remind you of anything from geometry?