20.5: Pigeonhole Principle

Theorem \(\PageIndex{1}\): Pigeonhole Principle (formal version).

If \(A,B\) are finite sets with \(\vert B \vert \lt \vert A \vert\text{,}\) then no function \(A \to B\) can be an injection.

Proof.

This principle is just the contrapositive of Statement 2 of Fact 12.2.3.

Corollary \(\PageIndex{1}\): Pigeonhole Principle.

If \(m\) objects are placed in \(n\) containers, where \(m \gt n\text{,}\) then at least one container must contain more than one object.

Proof.

Let \(A\) be the set of objects and \(B\) the set of containers, so that

\begin{equation*} \vert B \vert = n \lt m = \vert A \vert \text{.} \end{equation*}
Also let \(f: A \rightarrow B\) represent the function where \(f(a) = b\) means that object \(a\) has been placed in container \(b\text{.}\) Then the Theorem \(\PageIndex{1}\) tells us that \(f\) cannot be an injection, which means that there is at least one pair of distinct objects \(a_1,a_2\) with \(f(a_1) = f(a_2)\text{.}\)

Example \(\PageIndex{1}\): Too few seats.

Your car has five seats, but you also have five friends who need a ride home. How will everyone fit?

Solution

Using the people who need to get home (i.e. your friends and you) as objects and car seats as containers, Pigeonhole Principle says that someone will have to sit on someone else's lap.

Example \(\PageIndex{2}\): Dessert logistics.

The cafeteria puts out \(200\) chocolate puddings and \(200\) tapioca puddings. If \(201\) students each grab a bowl of pudding, what is the minimum number of tapioca puddings that have been taken?

Solution

Since \(201 \gt 200\text{,}\) there is no injection

\begin{equation*} \{\text{students who took a pudding}\} \hookrightarrow \{\text{bowls of chocolate pudding}\} \text{.} \end{equation*}
(Or: use students as objects, bowls of chocolate pudding as containers.)

But we can't actually have two students take the same bowl of pudding, so at least one student must eat tapioca.

Example \(\PageIndex{3}\): Matching pairs.

Suppose \(A \subseteq \{1,2,\cdots, 20\}\text{.}\) How big must \(\vert A \vert\) be to ensure that there exist two elements of \(A\) whose sum is \(21\text{?}\)

Solution

Collect together the (unordered) pairs of numbers that add to \(21\text{:}\)

\begin{equation*} B = \bigl\{ \{1,20\}, \{2,19\}, \cdots, \{10,11\} \bigr\} \subseteq \mathscr{P} (\{1,2,\cdots, 20\}) \text{.} \end{equation*}
Notice that \(\vert B \vert = 10\text{.}\) Thinking of the elements of \(B\) as containers and elements of \(A\) as objects, place object \(a\) into container \(b\) if \(a \in b\text{.}\) We need one more object than container to ensure some container receives two objects, so the answer is \(\vert A \vert \ge 11\text{.}\)

Example \(\PageIndex{4}\): Matching modulo \(m\).

Suppose \(m \in \mathbb{N}\) and \(A \subseteq \mathbb{N}\) such that \(0 \lt m \lt \vert A \vert \lt \infty\text{.}\) Show that there exist distinct \(a_1,a_2 \in A\) that have the same remainder when divided by \(m\text{.}\)

Solution

The set of possible remainders is \(\mathbb{N}_{<m} = \{0,1,2,\cdots,m-1\}\text{.}\) Computing remainder after division by \(m\) defines a function \(A \to \mathbb{N}_{<m}\text{.}\) Since \(\vert \mathbb{N}_{<m} \vert = m \lt \vert A \vert\text{,}\) this function cannot be an injection.

(Or: use elements of \(A\) as objects, possible remainders when dividing a number by \(m\) as containers.)

Strong version

Recall that given a function \(f: A \rightarrow B\text{,}\) we can define an equivalence relation \(\mathord{\equiv}\) on \(A\) by taking \(a_1 \equiv a_2\) to mean \(f(a_1) = f(a_2)\) (see Example 18.4.4). In this way, we can regard \(f\) as placing objects (elements of \(A\)) into containers (elements of \(B\)), so that object \(a \in A\) is “placed” in container \(b \in B\) when \(f(a) = b\text{.}\)

Theorem \(\PageIndex{3}\): Pigeonhole Principle (strong form, formal version).

Suppose \(f: A \rightarrow B\text{,}\) with \(A,B\) finite, and let \(\mathord{\equiv}\) be the equivalence relation on \(A\) where \(a_1 \equiv a_2\) means \(f(a_1) = f(a_2)\text{.}\)

If \(\vert A \vert \gt \ell \cdot \vert B \vert\) for some \(\ell \in \mathbb{N}\text{,}\) then at least one of the equivalence classes of \(A\) with respect to \(\mathord{\equiv}\) has more than \(\ell\) elements.

Proof.

Consider the contrapositive:

if every equivalence class of \(A\) has no more than \(\ell\) elements, then \(\vert A \vert \le \ell \cdot \vert B \vert\text{.}\)

Since \(B\) is finite and \(f(A) \subseteq B\text{,}\) then also \(f(A)\) is finite and we can enumerate its elements. Write \(f(A) = \{ b_1, b_2, \cdots, b_n \}\text{.}\) Each element of \(f(A)\) corresponds to an equivalence class of \(A\text{.}\)

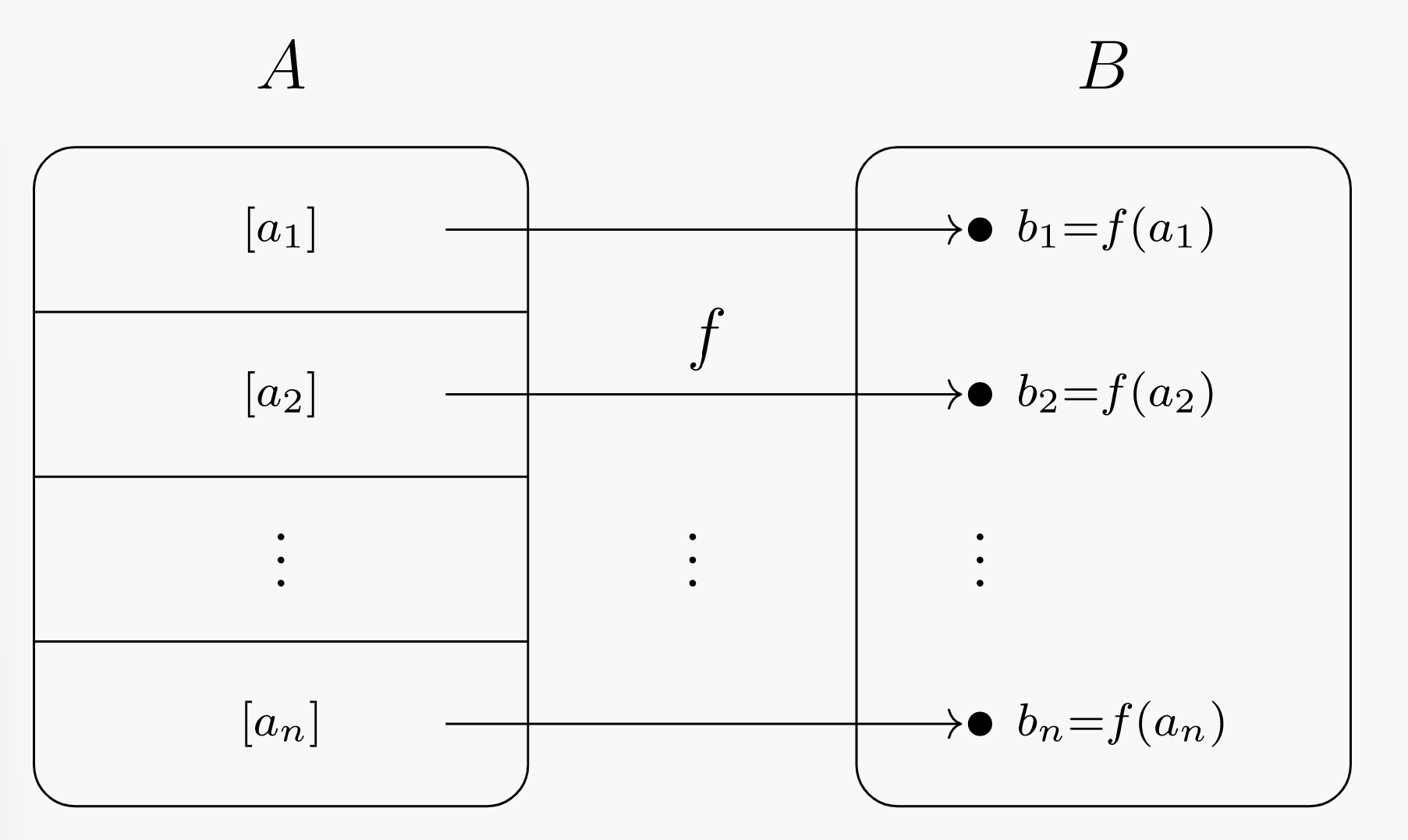
Figure \(\PageIndex{1}\): Diagram of equivalence classes under the “have same image” equivalence.

In this diagram, the \(a_i\) are representative elements of the class of elements of \(A\) that are mapped to \(b_i\) by \(f\text{.}\) In particular, we must have \(f(a_i) = b_i\) for each index \(i\text{.}\)

We are assuming that each class \([a_i]\) contains no more than \(\ell\) elements; i.e. \(\vert [a_i] \vert \le \ell\text{.}\) Since an equivalence relation always partitions a set \(A\) into the disjoint union of its equivalence classes, we have

\begin{align*} \vert A \vert & = \vert [a_1] \vert + \vert [a_2] \vert + \cdots + \vert [a_n] \vert \\ & \le \underbrace{\ell + \ell + \cdots + \ell}_{r \text{ terms}} \\ & = \ell n \\ & = \ell \cdot \vert f(A) \vert. \end{align*}
But \(f(A)\) is a subset of the finite set \(B\text{,}\) and so \(\vert f(A) \vert \le \vert B \vert\text{.}\) Combining this with the calculation above gives

\begin{equation*} \vert A \vert \le \ell \cdot \vert f(A) \vert \le \ell \cdot \vert B \vert \text{.} \end{equation*}

Corollary \(\PageIndex{2}\): Pigeonhole Principle (strong form, informal version).

If \(m\) objects are placed in \(n\) containers, with \(m \gt \ell n \) for some \(\ell \in \mathbb{N}\text{,}\) then at least one container contains more than \(\ell\) objects.

Proof Idea.

Again, let \(A\) be the set of objects and \(B\) the set of containers, so that

\begin{equation*} \vert A \vert = m \gt \ell n = \ell \cdot \vert B \vert \text{.} \end{equation*}
Then apply the Pigeonhole Principle (strong form, formal version).

Note \(\PageIndex{1}\)

The Pigeonhole Principle (strong form, formal version) is a generalization of the Pigeonhole Principle (formal version). A function is an injection precisely when no two distinct elements of the domain produce the same output image, so using \(\ell = 1\) in the strong form gives back the original form.

Example \(\PageIndex{5}\): Handing out coins.

Show that if thirteen coins are distributed to six children, then at least one child will receive at least three coins.

Solution

Using coins as objects and children as containers, the given statement is just the Pigeonhole Principle (strong form, formal version) with \(\ell = 2\text{:}\) we have \(13\) objects and \(6\) containers, and \(13 \gt 2 \cdot 6\text{.}\) (Note: Since coins are discrete objects, “more than two” and “at least three” are the same thing.)

Remark \(\PageIndex{1}\)

It is worthwhile to think about how the strong form of the Pigeonhole Principle could be proved directly. Consider the diagram in Figure \(\PageIndex{1}\): the “tipping point” between \(\vert A \vert \le \ell \cdot \vert B \vert\) and \(\vert A \vert \gt \ell \cdot \vert B \vert\) is when \(f\) is surjective and each of the equivalence classes has exactly \(\ell\) elements. When \(f\) is surjective, there are \(\vert B \vert\) equivalence classes in \(A\text{.}\) Since \(A\) is the disjoint union of its equivalence classes under \(\equiv\text{,}\) we have \(\vert A \vert = \ell \cdot \vert B \vert\text{.}\) If we add one more element to \(A\text{,}\) it will have to be included in one of the equivalence classes, and that class will now have size greater than \(\ell\text{.}\)

Example \(\PageIndex{6}\): Handing out pudding.

The cafeteria puts out \(100\) chocolate, \(100\) tapioca, and \(100\) butterscotch puddings. How many students must grab a pudding before we can be certain that at least one of the flavours has at least half of the bowls taken?

Solution. 1 Using “tipping point” thinking
The “tipping point” is exactly \(49\) bowls of each flavour taken, which requires \(3\cdot 49 = 147\) students. After the \(148^{th}\) student, we will definitely have \(50\) bowls of one of the flavours taken.

Solution. 2 Direct use of the Pigeonhole Principle
Consider students as objects (\(m\) of them — this is the unknown to be determined) and flavours as containers (\(3\) of them). To determine the appropriate value of \(\ell\) to use, consider that “at least half” in this problem means “at least \(50\)”, which is the same as “more than \(49\)”. So choose \(\ell = 49\text{.}\) In that case, we need \(m \gt 49 \cdot 3 = 147\text{,}\) bringing us to the answer of \(m = 147 + 1 = 148\) students.