21.4: Permutations of Subsets

Sometimes we want to create an ordered list of a certain length from a larger pool of candidates.

Definition: Permutation of size \(k\)

an ordered list of \(k\) elements from a given set \(A\text{,}\) with \(\vert A \vert \ge k\)

Definition: \(P(n, k)\)

the number of permutations of size \(k\) taken from a set of size \(n\)

Definition: \(P^n_k\text{,}\) \(_nP_k\)

alternative notation choices for \(P(n, k)\)

Example \(\PageIndex{1}\): Visualizing \(P(4, 2)\).

Consider \(A = \{1,2,3,4\}\text{,}\) so that \(n = \vert A \vert = 4\text{.}\) There are \(4! = 24 \) permutations of \(A\text{.}\)

Figure \(\PageIndex{1}\): Permutations of a set of size \(4\text{.}\)

Notice that the permutations above have been grouped into pairs, where the two permutations in a given pair have the same two first elements in the same order. From this, we can conclude that there are only \(24/2 = 12\) permutations of size \(k=2\) from \(A\text{.}\)

Theorem \(\PageIndex{1}\): Computing \(P(n, k)\).

We have

\begin{equation*} P(n, k) = \dfrac{n!}{(n-k)!} = n (n-1) (n-2) \cdots (n-k+1) \text{.} \end{equation*}

Proof.

One way to construct an ordered list of \(k\) elements from a set \(A\text{,}\) where \(\vert A \vert = n\text{,}\) is as in Example \(\PageIndex{1}\). Form an ordered list of all the elements of \(A\) (\(n!\) ways), and then take the first \(k\) elements from that list. But we get the same ordered list of length \(k\) no matter how the last \(n-k\) elements are ordered. That is, we consider any two orderings of all \(n\) elements to be equivalent if the first \(k\) elements in the list are the same between the two. As there are \((n-k)!\) different ways the last \(n - k\) elements could be ordered while keeping the first \(k\) elements the same, each equivalence class has size \((n - k)!\text{.}\) Applying the Division Rule, we obtain the desired formula

\begin{equation*} P(n, k) = \dfrac{\# \{ \text{orderings of all } n \text{ elements} \} }{\# \{ \text{reorderings of the last } n - k \text{ elements} \} } = \dfrac{n!}{(n - k)!}\text{.} \end{equation*}

Remark \(\PageIndex{1}\)

The number \(P(n,n)\) represents the number of ways to construct an ordered list of \(n\) elements chosen from a set of \(n\) elements, so \(P(n,n) = n!\text{.}\) The convention \(0! = 1\) ensures that our formula for \(P(n,k)\) expressed in Theorem \(\PageIndex{1}\) remains valid in the case \(k = n\text{.}\)

Example \(\PageIndex{2}\): Elections.

A class of twenty discrete mathematics students decides to elect a class president and vice-president. How many possible outcomes to the election process are there?

Solution

An arbitrary way to elect students to these offices would be to line all the students up and choose the first two students in line to be the president and vice-president, respectively. Therefore, there are

\begin{equation*} P(20, 2) = \dfrac{20!}{(20 - 2)!} = 20 \cdot 19 = 380 \end{equation*}
possible outcomes to the election.

Example \(\PageIndex{3}\): Ranking choices.

You go to the horsetrack to bet on a race. From a field of nine horses, how many ways are there to make a “Trifecta” bet (i.e. specify the first three finishers in order)?

Solution

There are

\begin{equation*} P(9, 3) = \dfrac{9!}{(9 - 3)!} = 9 \cdot 8 \cdot 7 = 504 \end{equation*}
possible such bets.

Example \(\PageIndex{4}\): Words with no repeated letters.

For alphabet \(\Sigma = \{a, b, c, \ldots, y, z\}\text{,}\) how many four-letter words made up of distinct letters are there in \(\Sigma^{\ast}\text{?}\)

Compare.

See Worked Example 20.3.6.

Solution

A four-letter word with no repeated letters is the same as a permutation of size \(4\text{,}\) so the number of such words is

\begin{equation*} P(26, 4) = \dfrac{26!}{(26 - 4)!} = 26 \cdot 25 \cdot 24 \cdot 23 = 358,800 \text{.} \end{equation*}

Example \(\PageIndex{5}\)

If \(\vert A \vert = k\) and \(\vert B \vert = n\text{,}\) with \(k \le n\text{,}\) how many injective functions \(f: A \rightarrow B\) exist?

Compare.

See Worked Example 20.3.9.

Solution

Fix an ordering \(a_1,a_2,\ldots,a_k\) of the elements of \(A\text{.}\) Then from any ordering \(b_1, b_2, \ldots, b_k\) of size \(k\) from \(B\text{,}\) we get an injective function \(f: A \hookrightarrow B\) by the following table of values.

Figure \(\PageIndex{2}\)

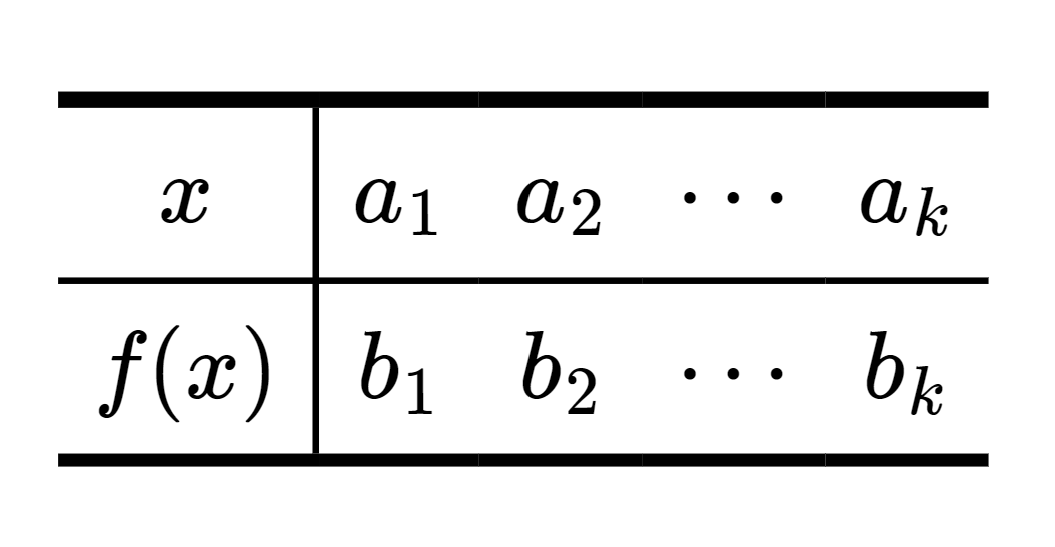
That is, every permutation of \(B\) of size \(k\) corresponds to an injection \(f: A \hookrightarrow B \text{,}\) and so the number of such injections is \(P(n, k)\text{.}\)