23.1: Bionomial Coefficients
- Page ID
- 83517
an expression of the form \((x + y)^n\text{,}\) where \(n \in \mathbb{N}\) and \(x,y\) are real numbers (or elements of any commutative ring with identity)
Expanding binomials gets more complicated as \(n\) increases.
\begin{align*} (x + y)^2 & = x^2 + 2 x y + y^2 \\ (x + y)^3 & = (x + y) (x^2 + 2 x y + y^2) = x^3 + 3 x^2 y + 3 x y^2 + y^3 \\ (x + y)^4 & = (x + y) (x^3 + 3 x^2 y + 3 x y^2 + y^3) = x^4 + 4 x^3 y + 6 x^2 y^2 + 4 x y^3 + y^4 \\ (x + y)^5 & = (x + y) (x^4 + 4 x^3 y + 6 x^2 y^2 + 4 x y^3 + y^4) \\ & = x^5 + 5 x^4 y + 10 x^3 y^2 + 10 x^2 y^3 + 5 x y^4 + y^5 \\ & \vdots \end{align*}
The symmetry in each of these expansions should be expected: we would get the same expression in the summation opposite order if we swapped \(x\) and \(y\text{,}\) since \((x + y)^n = (y + x)^n\text{.}\)
a number appearing as a coefficient in the expansion of \((x + y)^n\)
the \(k^{th}\) coefficient in the expansion of \((x + y)^n\) (\(0 \le k \le n\))
To better understand the complexity of binomial expansions, we should look for and exploit patterns. We have already expanded some binomial expressions for small exponents in Example \(\PageIndex{1}\) — let's extract the binomial coefficients from those expressions.
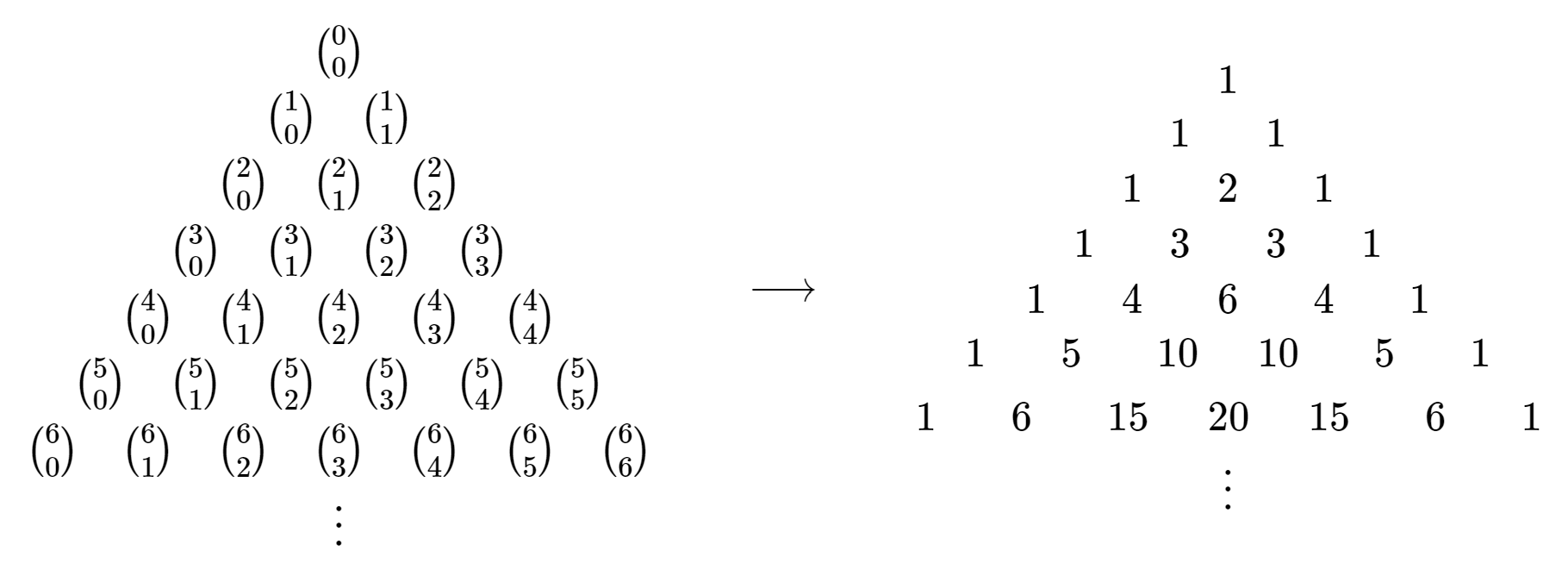
Figure \(\PageIndex{1}\) above sure looks a lot like Figure 22.4.1.
For every \(x,y\in\mathbb{R}\) and every \(n \in \mathbb{N}\text{,}\) we have
\begin{equation*} (x+y)^n = \sum_{k=0}^n \binom{n}{k}\,x^{n-k}y^k = \binom{n}{0}\,x^n + \binom{n}{1}\,x^{n-1}y + \binom{n}{2}\,x^{n-2}y^2 + \cdots + \binom{n}{n-1}\,xy^{n-1} + \binom{n}{n}\,y^n, \end{equation*}
where
\begin{equation*} \binom{n}{k} = C^n_k = \dfrac{n!}{k! (n-k)!} \text{.} \end{equation*}
- Informal direct proof outline.
-
Write \((x+y)^n = (x+y)(x+y)\cdots(x+y)\text{,}\) with \(n\) factors. To expand this out, we generalize the FOIL method: from each factor, choose either \(x\) or \(y\text{,}\) then multiply all your choices together. Then add the results of all possible such products. For example,
\begin{align*} (x + y)^2 & = x x + x y + y x + y y = x^2 + 2 x y + y^2, \\ (x + y)^3 & = x x x + x x y + x y x + x y y + y x x + y x y + y y x + y y y = x^3 + 3 x^2y + 3 x y^2 + y^3. \end{align*}
When forming a specific product, if you chose \(y\) for \(k\) out of \(n\) choices, you must have chosen \(x\) for the remaining \(n - k\) of the \(n\) choices. The result will be \(x^{n - k} y^k\text{.}\) So to figure out the coefficient on \(x^{n - k} y^k\text{,}\) just count how many ways there are to choose \(y\) for \(k\) of the \(n\) choices. This is just \(C^n_k\text{,}\) where we choose \(k\) factors of \((x+y)\) to give us a \(y\text{,}\) and the rest to give us an \(x\text{.}\)
- Induction proof outline.
-
Base case.
The cases of \(n=0,1\) are trivially true.Induction step.
Use the binomial formula for \((x+y)^{n - 1}\) to obtain the binomial formula for \((x + y)^n\text{,}\) by manipulating\begin{align*} (x + y)^n & = (x + y) (x + y)^{n - 1} \\ & = (x + y) ( C^{n-1}_0 \, x^{n - 1} + C^{n-1}_1 \, x^{n - 2} y + \cdots + C^{n-1}_{n-1} \, y^{n - 1} )\text{.} \end{align*}
Expand \((x-2)^5\text{.}\)
Solution
We saw that the \(n = 5\) row of Pascal's triangle is \(1,5,10,10,5,1\text{.}\)
\begin{align*} & (x - 2)^5 \\ & (x + (- 2))^5 \\ & = \binom{5}{0} x^5 + \binom{5}{1} x^4 (-2) + \binom{5}{2} x^3 (-2)^2 + \binom{5}{3} x^2 (-2)^3 + \binom{5}{4} x (-2)^4 + \binom{5}{5} (-2)^5\\ & = x^5 - 10 x^4 + 40 x^3 - 80 x^2 + 80 x - 32. \end{align*}
What is the coefficient on the \(x^4 y^9\) term in the expansion of \((3 x + y)^{13} \text{?}\)
Solution
Considering
\begin{equation*} (3 x + y)^{13} = ((3 x) + y)^{13} \text{,} \end{equation*}
the \(x^4 y^9\) term is
\begin{align*} \binom{13}{9} (3x)^4 y^9 & = \dfrac{13!}{9!4!} \cdot 3^4 x^4 y^9\\ & = \dfrac{13 \cdot 12 \cdot 11 \cdot 10 \cdot 27 \cdot 3}{4\cdot 3 \cdot 2} x^4 y^9 \\ & = (13 \cdot 3 \cdot 11 \cdot 5 \cdot 27) x^4 y^9 \text{.} \end{align*}
So the desired coefficient is \(57,915\text{.}\)


