1.1: Free Fall
- Page ID
- 91046
In this chapter we will study some common differential equations that appear in physics. We will begin with the simplest types of equations and standard techniques for solving them We will end this part of the discussion by returning to the problem of free fall with air resistance. We will then turn to the study of oscillations, which are modeled by second order differential equations.
Free fall example.
Let us begin with a simple example from introductory physics. Recall that free fall is the vertical motion of an object solely under the force of gravity. It has been experimentally determined that an object near the surface of the Earth falls at a constant acceleration in the absence of other forces, such as air resistance. This constant acceleration is denoted by \(-g\), where \(g\) is called the acceleration due to gravity. The negative sign is an indication that we have chosen a coordinate system in which up is positive.
We are interested in determining the position, \(y(t)\), of the falling body as a function of time. From the definition of free fall, we have
\[\ddot{y}(t)=-g \label{1.1}. \]
Note that we will occasionally use a dot to indicate time differentiation.
Differentiation with respect to time is often denoted by dots instead of primes.
This notation is standard in physics and we will begin to introduce you to this notation, though at times we might use the more familiar prime notation to indicate spatial differentiation, or general differentiation.
In Equation \(\PageIndex{1}\) we know \(g\). It is a constant. Near the Earth’s surface it is about \(9.81 \mathrm{~m} / \mathrm{s}^{2}\) or \(32.2 \mathrm{ft} / \mathrm{s}^{2}\). What we do not know is \(y(t)\). This is our first differential equation. In fact it is natural to see differential equations appear in physics often through Newton’s Second Law, \(F=m a\), as it plays an important role in classical physics. We will return to this point later.
So, how does one solve the differential equation in \(\PageIndex{1}\)? We do so by using what we know about calculus. It might be easier to see when we put in a particular number instead of \(g\). You might still be getting used to the fact that some letters are used to represent constants. We will come back to the more general form after we see how to solve the differential equation.
Consider
\[\ddot{y}(t)=5. \nonumber \]
Recalling that the second derivative is just the derivative of a derivative, we can rewrite this equation as
\[\dfrac{d}{d t}\left(\dfrac{d y}{d t}\right)=5 \nonumber \]
This tells us that the derivative of \(d y / d t\) is 5 . Can you think of a function whose derivative is 5 ? (Do not forget that the independent variable is \(t\).) Yes, the derivative of \(5 t\) with respect to \(t\) is 5 . Is this the only function whose derivative is 5 ? No! You can also differentiate \(5 t+1,5 t+\pi, 5 t-6\), etc. In general, the derivative of \(5 t+C\) is 5, where \(C\) is an arbitrary integration constant.
So, Equation \(\PageIndex{2}\) can be reduced to
\[\dfrac{d y}{d t}=5 t+C \nonumber \]
Now we ask if you know a function whose derivative is \(5 t+C\). Well, you might be able to do this one in your head, but we just need to recall the Fundamental Theorem of Calculus, which relates integrals and derivatives. Thus, we have
\[y(t)=\dfrac{5}{2} t^{2}+C t+D \nonumber \]
where \(D\) is a second integration constant.
Equation \(\PageIndex{5}\) gives the solution to the original differential equation. That means that when the solution is placed into the differential equation, both sides of the differential equation give the same expression. You can always check your answer to a differential equation by showing that your solution satisfies the equation. In this case we have
\(\ddot{y}(t)=\dfrac{d^{2}}{d t^{2}}\left(\dfrac{5}{2} t^{2}+C t+D\right)=\dfrac{d}{d t}(5 t+C)=5\)
Therefore, Equation \(\PageIndex{5}\) gives the general solution of the differential equation.
We also see that there are two arbitrary constants, \(C\) and \(D .\) Picking any values for these gives a whole family of solutions. As we will see, the equation \(\ddot{y}(t)=5\) is a linear second order ordinary differential equation. The general solution of such an equation always has two arbitrary constants.
Let’s return to the free fall problem. We solve it the same way. The only difference is that we can replace the constant 5 with the constant \(-g .\) So, we find that
\[\dfrac{d y}{d t}=-g t+C \nonumber \]
and
\[y(t)=-\dfrac{1}{2} g t^{2}+C t+D \nonumber \]
Once you get down the process, it only takes a line or two to solve.
There seems to be a problem. Imagine dropping a ball that then undergoes free fall. We just determined that there are an infinite number of solutions for the position of the ball at any time! Well, that is not possible. Experience tells us that if you drop a ball you expect it to behave the same way every time. Or does it? Actually, you could drop the ball from anywhere. You could also toss it up or throw it down. So, there are many ways you can release the ball before it is in free fall producing many different paths, \(y(t)\). That is where the constants come in. They have physical meanings.
If you set \(t=0\) in the equation, then you have that \(y(0)=D .\) Thus, \(D\) gives the initial position of the ball. Typically, we denote initial values with a subscript. So, we will write \(y(0)=y_{0}\). Thus, \(D=y_{0}\).
That leaves us to determine \(C\). It appears at first in Equation \(\PageIndex{6}\). Recall that \(\dfrac{d y}{d t}\), the derivative of the position, is the vertical velocity, \(v(t)\). It is positive when the ball moves upward. We will denote the initial velocity \(v(0)=v_{0} .\) Inserting \(t=0\) in Equation \(\PageIndex{6}\), we find that \(\dot{y}(0)=C\). This implies that \(C=v(0)=v_{0}\).
Putting this all together, we have the physical form of the solution for free fall as
\[y(t)=-\dfrac{1}{2} g t^{2}+v_{0} t+y_{0} \nonumber \]
Doesn’t this equation look familiar? Now we see that the infinite family of solutions consists of free fall resulting from initially dropping a ball at position \(y_{0}\) with initial velocity \(v_{0}\). The conditions \(y(0)=y_{0}\) and \(\dot{y}(0)=v_{0}\) are called the initial conditions. A solution of a differential equation satisfying a set of initial conditions is often called a particular solution. Specifying the initial conditions results in a unique solution.
So, we have solved the free fall equation. Along the way we have begun to see some of the features that will appear in the solutions of other problems that are modeled with differential equation. Throughout the book we will see several applications of differential equations. We will extend our analysis to higher dimensions, in which we case will be faced with socalled partial differential equations, which involve the partial derivatives of functions of more that one variable.
But are we done with free fall? Not at all! We can relax some of the conditions that we have imposed. We can add air resistance. We will visit this problem later in this chapter after introducing some more techniques. We can also provide a horizontal component of motion, leading to projectile motion.
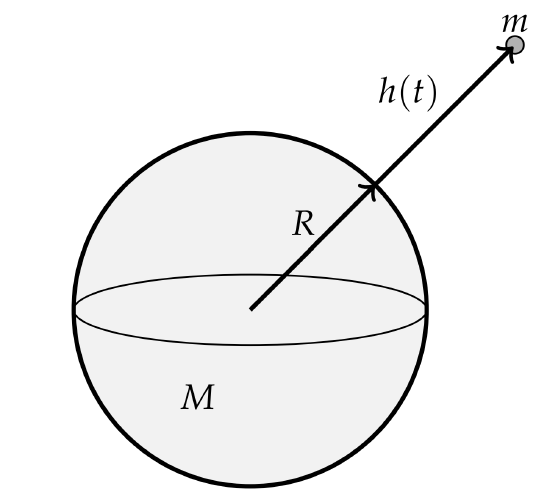
Finally, we should also note that free fall at constant \(g\) only takes place near the surface of the Earth. What if a tile falls off the shuttle far from the surface of the Earth? It will also fall towards the Earth. Actually, the tile also has a velocity component in the direction of the motion of the shuttle. So, it would not necessarily take radial path downwards. For now, let’s ignore that component. To look at this problem in more detail, we need to go to the origins of the acceleration due to gravity. This comes out of Newton’s Law of Gravitation. Consider a mass \(m\) at some distance \(h(t)\) from the surface of the (spherical) Earth. Letting \(M\) and \(R\) be the Earth’s mass and radius, respectively, Newton’s Law of Gravitation states that
\[ \begin{aligned} m a &=F \\ m \dfrac{d^{2} h(t)}{d t^{2}} &=-G \dfrac{m M}{(R+h(t))^{2}} \end{aligned} \nonumber \]
Here \(G=6.6730 \times 10^{-11} \mathrm{~m}^{3} \mathrm{~kg}^{-1} \mathrm{~s}^{-2}\) is the Universal Gravitational Constant, \(M=5.9736 \times 10^{24} \mathrm{~kg}\) and \(R=6371 \mathrm{~km}\) are the Earth’s mass and mean radius, respectively. For \(h<<R, G M / R^{2} \approx g\).
Thus, we arrive at a differential equation
\[\dfrac{d^{2} h(t)}{d t^{2}}=-\dfrac{G M}{(R+h(t))^{2}} . \nonumber \]
This equation is not as easy to solve. We will leave it as a homework exercise for the reader.


