8.4: Limit cycles
- Page ID
- 3420
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)For nonlinear systems, trajectories do not simply need to approach or leave a single point. They may in fact approach a larger set, such as a circle or another closed curve.
The Van der Pol oscillator\(^{1}\) is the following equation
\[x''-\mu(1-x^2) x' + x = 0, \nonumber \]
where \(\mu\) is some positive constant. The Van der Pol oscillator originated with electrical circuits, but finds applications in diverse fields such as biology, seismology, and other physical sciences.
For simplicity, let us use \(\mu = 1\). A phase diagram is given in the left hand plot in Figure \(\PageIndex{1}\). Notice how the trajectories seem to very quickly settle on a closed curve. On the right hand plot we have the plot of a single solution for \(t=0\) to \(t=30\) with initial conditions \(x(0) = 0.1\) and \(x'(0) = 0.1\). Notice how the solution quickly tends to a periodic solution.
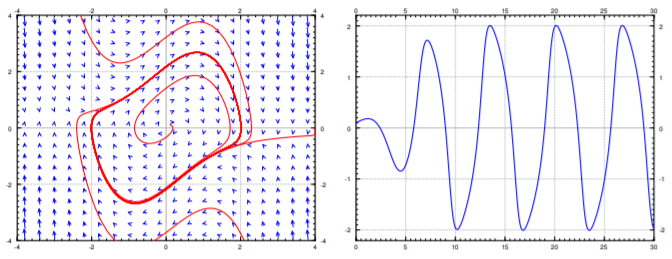
The Van der Pol oscillator is an example of so-called relaxation oscillation. The word relaxation comes from the sudden jump (the very steep part of the solution). For larger \(\mu\) the steep part becomes even more pronounced, for small \(\mu\) the limit cycle looks more like a circle. In fact setting \(\mu = 0\), we get \(x''+x=0\), which is a linear system with a center and all trajectories become circles.
The closed curve in the phase portrait above is called a limit cycle. A limit cycle is a closed trajectory such that at least one other trajectory spirals into it (or spirals out of it). If all trajectories that start near the limit cycle spiral into it, the limit cycle is called asymptotically stable. The limit cycle in the Van der Pol oscillator is asymptotically stable.
Given a limit cycle on an autonomous system, any solution that starts on it is periodic. In fact, this is true for any trajectory that is a closed curve (a so-called closed trajectory). Such a curve is called a periodic orbit. More precisely, if \(\bigl(x(t),y(t)\bigr)\) is a solution such that for some \(t_0\) the point \(\bigl(x(t_0),y(t_0)\bigr)\) lies on a periodic orbit, then both \(x(t)\) and \(y(t)\) are periodic functions (with the same period). That is, there is some number \(P\) such that \(x(t) = x(t+P)\) and \(y(t) = y(t+P)\).
Consider the system
\[\label{eq:2} x' = f(x,y), ~~~~~ y' = g(x,y) , \]
where the functions \(f\) and \(g\) have continuous derivatives in some region \(R\) in the plane.
Suppose \(R\) is a closed bounded region (a region in the plane that includes its boundary and does not have points arbitrarily far from the origin). Suppose \(\bigl(x(t), y(t)\bigr)\) is a solution of \(\eqref{eq:2}\) in \(R\) that exists for all \(t \geq t_0\). Then either the solution is a periodic function, or the solution spirals towards a periodic solution in \(R\).
The main point of the theorem is that if you find one solution that exists for all \(t\) large enough (that is, as \(t\) goes to infinity) and stays within a bounded region, then you have found either a periodic orbit, or a solution that spirals towards a limit cycle or tends to a critical point. That is, in the long term, the behavior is very close to a periodic function. Note that a constant solution at a critical point is periodic (with any period). The theorem is more a qualitative statement rather than something to help us in computations. In practice it is hard to find analytic solutions and so hard to show rigorously that they exist for all time. But if we think the solution exists we numerically solve for a large time to approximate the limit cycle. Another caveat is that the theorem only works in two dimensions. In three dimensions and higher, there is simply too much room.
The theorem applies to all solutions in the Van der Pol oscillator. Solutions that start at any point except the origin \((0,0)\) will tend to the periodic solution around the limit cycle, and if the initial condition of \((0,0)\) will lead to the constant solution \(x=0\), \(y=0\).
Consider \[x' = y + {(x^2+y^2-1)}^2 x, \qquad y' = -x + {(x^2+y^2-1)}^2 y. \nonumber \] A vector field along with solutions with initial conditions \((1.02,0)\), \((0.9,0)\), and \((0.1,0)\) are drawn in Figure \(\PageIndex{2}\).
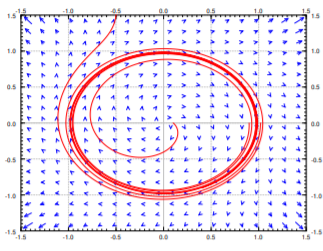
Notice that points on the unit circle (distance one from the origin) satisfy \(x^2+y^2-1=0\). And \(x(t) = \sin(t)\), \(y = \cos(t)\) is a solution of the system. Therefore we have a closed trajectory. For points off the unit circle, the second term in \(x'\) pushes the solution further away from the \(y\)-axis than the system \(x' = y\), \(y' = -x\), and \(y'\) pushes the solution further away from the \(x\)-axis than the linear system \(x'=y\), \(y' = -x\). In other words for all other initial conditions the trajectory will spiral out.
This means that for initial conditions inside the unit circle, the solution spirals out towards the periodic solution on the unit circle, and for initial conditions outside the unit circle the solutions spiral off towards infinity. Therefore the unit circle is a limit cycle, but not an asymptotically stable one. The Poincaré–Bendixson Theorem applies to the initial points inside the unit circle, as those solutions stay bounded, but not to those outside, as those solutions go off to infinity.
A very similar analysis applies to the system \[x' = y + {(x^2+y^2-1)} x, \qquad y' = -x + {(x^2+y^2-1)} y. \nonumber \] We still obtain a closed trajectory on the unit circle, and points outside the unit circle spiral out to infinity, but now points inside the unit circle spiral towards the critical point at the origin. So this system does not have a limit cycle, even though it has a closed trajectory.
Due to the Picard theorem (3.1.1) we find that no matter where we are in the plane we can always find a solution a little bit further in time, as long as \(f\) and \(g\) have continuous derivatives. So if we find a closed trajectory in an autonomous system, then for every initial point inside the closed trajectory, the solution will exist for all time and it will stay bounded (it will stay inside the closed trajectory). So the moment we found the solution above going around the unit circle, we knew that for every initial point inside the circle, the solution exists for all time and the Poincaré–Bendixson theorem applies.
Let us next look for conditions when limit cycles (or periodic orbits) do not exist. We assume the equation \(\eqref{eq:2}\) is defined on a simply connected region, that is, a region with no holes we can go around. For example the entire plane is a simply connected region, and so is the inside of the unit disc. However, the entire plane minus a point is not a simply connected domain as it has a at the origin.
Suppose \(f\) and \(g\) are defined in a simply connected region \(R\). If the expression\(^{4}\)
\[ \frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} \nonumber \]
is either always positive or always negative on \(R\) (except perhaps a small set such as on isolated points or curves) then the system \(\eqref{eq:2}\) has no closed trajectory inside \(R\).
The theorem gives us a way of ruling out the existence of a closed trajectory, and hence a way of ruling out limit cycles. The exception about points or lines really means that we can allow the expression to be zero at a few points, or perhaps on a curve, but not on any larger set.
Let us look at \(x'=y+y^2e^x\), \(y'=x\) in the entire plane (see Example 8.2.2.) The entire plane is simply connected and so we can apply the theorem. We compute \(\frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} = y^2e^x+ 0\). The function \(y^2e^x\) is always positive except on the line \(y=0\). Therefore, via the theorem, the system has no closed trajectories.
In some books (or the internet) the theorem is not stated carefully and it concludes there are no periodic solutions. That is not quite right. The above example has two critical points and hence it has constant solutions, and constant functions are periodic. The conclusion of the theorem should be that there exist no trajectories that form closed curves. Another way to state the conclusion of the theorem would be to say that there exist no nonconstant periodic solutions that stay in \(R\).
Let us look at a somewhat more complicated example. Take the system \(x'=-y-x^2\), \(y'=-x+y^2\) (see Example 8.2.1). We compute \(\frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} = 2x + 2y\). This expression takes on both signs, so if we are talking about the whole plane we cannot simply apply the theorem. However, we could apply it on the set where \(x+y > 0\). Via the theorem, there is no closed trajectory in that set. Similarly, there is no closed trajectory in the set \(x+y < 0\). We cannot conclude (yet) that there is no closed trajectory in the entire plane. Perhaps half of it is in the set where \(x+y >0\) and the other half is in the set where \(x+y < 0\).
The key is to look at the set \(x+y=0\), or \(x=-y\). Let us make a substitution \(x=z\) and \(y=-z\) (so that \(x=-y\)). Both equations become \(z'=z-z^2\). So any solution of \(z'=z-z^2\), gives us a solution \(x(t)=z(t)\), \(y(t)=-z(t)\). In particular, any solution that starts out on the line \(x+y=0\), stays on the line \(x+y = 0\). In other words, there cannot be a closed trajectory that starts on the set where \(x+y > 0\) and goes through the set where \(x+y < 0\), as it would have to pass through \(x+y = 0\).
Consider \(x' = y+(x^2+y^2-1)x\), \(y' = -x +(x^2+y^2-1)y\), and consider the region \(R\) given by \(x^2+y^2 > \frac{1}{2}\). That is, \(R\) is the region outside a circle of radius \(\frac{1}{\sqrt{2}}\) centered at the origin. Then there is a closed trajectory in \(R\), namely \(x=\cos(t)\), \(y=\sin(t)\). Furthermore, \[\frac{\partial f}{\partial x} + \frac{\partial g}{\partial x} = 4x^2+4y^2-2 , \nonumber \] which is always positive on \(R\). So what is going on? The Bendixson–Dulac theorem does not apply since the region \(R\) is not simply connected—it has a hole, the circle we cut out!
Footnotes
[1] Named for the Dutch physicist Balthasar van der Pol (1889–1959).
[2] Ivar Otto Bendixson (1861–1935) was a Swedish mathematician.
[3] Henri Dulac (1870–1955) was a French mathematician.
[4] Usually the expression in the Bendixson–Dulac Theorem is \(\frac{\partial (\varphi f)}{\partial x}+\frac{\partial (\varphi g)}{\varphi y}\) for some continuously differentiable function \(\varphi\). For simplicity, let us just consider the case \(\varphi =1\).


