1.1: Examples
- Page ID
- 2128
Example 1.1.1:
\(u_y=0\), where \(u=u(x,y)\). All functions \(u=w(x)\) are solutions.
Example 1.1.2:
\(u_x=u_y\), where \(u=u(x,y)\). A change of coordinates transforms this equation into an equation of the first example. Set \(\xi=x+y,\ \eta=x-y\), then
$$
u(x,y)=u\left(\frac{\xi+\eta}{2},\frac{\xi-\eta}{2}\right)=:v(\xi,\eta).
$$
Assume \(u\in C^1\), then
$$
v_\eta=\frac{1}{2}(u_x-u_y).
$$
If \(u_x=u_y\), then \(v_\eta=0\) and vice versa, thus \(v=w(\xi)\) are solutions for arbitrary \(C^1\)-functions \(w(\xi)\). Consequently, we have a large class of solutions of the original partial differential equation: \(u=w(x+y)\) with an arbitrary \(C^1\)-function \(w\).
Example 1.1.3:
A necessary and sufficient condition such that for given \(C^1\)-functions \(M,\ N\) the integral
$$
\int_{P_0}^{P_1}\ M(x,y)dx+N(x,y)dy
$$
is independent of the curve which connects the points \(P_0\) with \(P_1\) in a simply connected domain \(\Omega\subset\mathbb{R}^2\) is that the partial differential equation (condition of integrability)
$$
M_y=N_x
$$
in \(\Omega\).
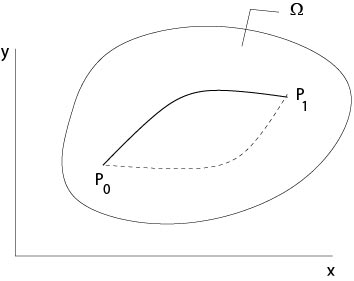
Figure 1.1.1: Independence of the path
This is one equation for two functions. A large class of solutions is given by \(M=\Phi_x,\ N=\Phi_y\), where \(\Phi(x,y)\) is an arbitrary \(C^2\)-function. It follows from Gauss theorem that these are all \(C^1\)-solutions of the above differential equation.
Example 1.1.4: Method of an integrating multiplier for an ordinary
differential
equation
Consider the ordinary differential equation
$$
M(x,y)dx+N(x,y)dy=0
$$
for given \(C^1\)-functions \(M,\ N\). Then we seek a \(C^1\)-function \(\mu(x,y)\) such that \(\mu Mdx+\mu Ndy\) is a total differential, i. e., that \((\mu M)_y=(\mu N)_x\) is satisfied. This is a linear partial differential equation of first order for \(\mu\):
$$
M\mu_y-N\mu_x=\mu (N_x-M_y).
\]
Example 1.1.5:
Two \(C^1\)-functions \(u(x,y)\) and \(v(x,y)\) are said to be functionally dependent if
$$
\det\left(\begin{array}{cc}u_x&u_y\\v_x&v_y\end{array}\right)=0,
$$
which is a linear partial differential equation of first order for \(u\) if \(v\) is a given \(C^1\)-function. A large class of solutions is given by
$$
u=H(v(x,y)),
$$
where \(H\) is an arbitrary \(C^1\)-function.
Example 1.1.6: Cauchy-Riemann equations
Set \(f(z)=u(x,y)+iv(x,y)\), where \(z=x+iy\) and \(u,\ v\) are given \(C^1(\Omega)\)-functions. Here \(\Omega\) is a domain in \(\mathbb{R}^2\). If the function \(f(z)\) is differentiable with respect to the complex variable \(z\) then \(u,\ v\) satisfy the Cauchy-Riemann equations
$$
u_x=v_y,\ \ u_y=-v_x.
$$
It is known from the theory of functions of one complex variable that the real part \(u\) and the imaginary part \(v\) of a differentiable function \(f(z)\) are solutions of the Laplace equation
$$
\triangle u=0,\ \ \triangle v=0,
$$
where \(\triangle u= u_{xx}+u_{yy}\).
Example 1.1.7: Newton Potential
The Newton potential
$$
u=\frac{1}{\sqrt{x^2+y^2+z^2}}
$$
is a solution of the Laplace equation in \(\mathbb{R}^3\setminus{(0,0,0)}\), that is, of
$$
u_{xx}+u_{yy}+u_{zz}=0.
\]
Example 1.1.8: Heat equation
Let \(u(x,t)\) be the temperature of a point \(x\in\Omega\) at time \(t\), where \(\Omega\subset\mathbb{R}^3\) is a domain. Then \(u(x,t)\) satisfies in \(\Omega\times[0,\infty)\) the heat equation
$$
u_t=k\triangle u,
$$
where \(\triangle u= u_{x_1x_1}+u_{x_2x_2}+u_{x_3x_3}\) and \(k\) is a positive constant. The condition
$$
u(x,0)=u_0(x),\ \ x\in \Omega,
$$
where \(u_0(x)\) is given, is an initial condition associated to the above heat equation. The condition
$$
u(x,t)=h(x,t),\ \ x\in \partial\Omega,\ t\ge0,
$$
where \(h(x,t)\) is given, is a boundary condition for the heat equation.
If \(h(x,t)=g(x)\), that is, \(h\) is independent of \(t\), then one expects that the solution \(u(x,t)\) tends to a function \(v(x)\) if \(t\to\infty\). Moreover, it turns out that \(v\) is the solution of the boundary value problem for the Laplace equation
\begin{eqnarray*}
\triangle v&=&0\ \ \mbox{in}\ \Omega\\
v&=&g(x)\ \ \mbox{on}\ \partial\Omega.
\end{eqnarray*}
Example 1.1.9: Wave equation
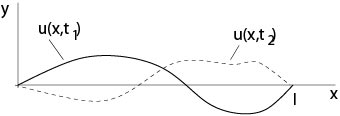
Figure 1.1.2: Oscillating string
The wave equation
$$
u_{tt}=c^2\triangle u,
$$
where \(u=u(x,t)\), \(c\) is a positive constant, describes oscillations of membranes or of three dimensional domains, for example. In the one-dimensional case
$$
u_{tt}=c^2 u_{xx}
$$
describes oscillations of a string.
Associated initial conditions are
$$
u(x,0)=u_0(x),\ \ u_t(x,0)=u_1(x),
$$
where \(u_0,\ u_1\) are given functions. Thus the initial position and the initial velocity are prescribed.
If the string is finite one describes additionally boundary conditions, for example
$$
u(0,t)=0,\ \ u(l,t)=0\ \ \mbox{for all}\ t\ge 0.
\]
Contributors and Attributions
Integrated by Justin Marshall.


