4.2.2: Case n=2
- Page ID
- 2178
Consider the initial value problem
\begin{eqnarray}
\label{n2dgl}\tag{4.2.2.1}
v_{xx}+v_{yy}&=&c^{-2}v_{tt}\\
\label{initial1} \tag{4.2.2.2}
v(x,y,0)&=&f(x,y)\\
\label{initial2} \tag{4.2.2.3}
v_t(x,y,0)&=&g(x,y),
\end{eqnarray}
where \(f\in C^3,\ g\in C^2\).
Using the formula for the solution of the three-dimensional initial value problem we will derive a formula for the two-dimensional case. The following consideration is called Hadamard's method of decent.
Let \(v(x,y,t)\) be a solution of (\ref{n2dgl})-(\ref{initial2}), then
$$u(x,y,z,t):=v(x,y,t)\]
is a solution of the three-dimensional initial value problem with initial data \(f(x,y)\), \(g(x,y)\), independent of \(z\), since \(u\) satisfies (\ref{n2dgl})-(\ref{initial2}). Hence, since \(u(x,y,z,t)=u(x,y,0,t)+u_z(x,y,\delta z,t)z\), \(0<\delta<1\), and \(u_z=0\), we have
$$v(x,y,t)=u(x,y,0,t).\]
Poisson's formula in the three-dimensional case implies
\begin{eqnarray}
v(x,y,t)&=&\frac{1}{4\pi c^2}\frac{\partial}{\partial t}\left(\frac{1}{t}\int_{\partial B_{ct}(x,y,0)}\ f(\xi,\eta)\ dS\right)\nonumber\\
\label{poissonhilf1} \tag{4.2.2.4}
&&+\frac{1}{4\pi c^2 t} \int_{\partial B_{ct}(x,y,0)}\ g(\xi,\eta)\ dS.
\end{eqnarray}
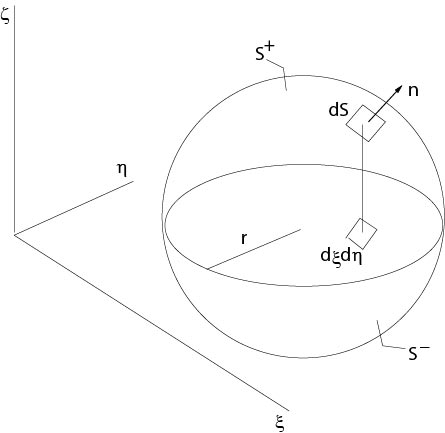
Figure 4.2.2.1: Domains of integration
The integrands are independent on \(\zeta\). The surface \(S\) is defined by \(\chi(\xi,\eta,\zeta):=(\xi-x)^2+(\eta-y)^2+\zeta^2-c^2 t^2=0\). Then the exterior normal \(n\) at \(S\) is \(n=\nabla\chi/|\nabla\chi|\) and the surface element is given by \(dS=(1/|n_3|)d\xi d\eta\), where the third coordinate of \(n\) is
$$n_3=\pm\frac{\sqrt{c^2 t^2-(\xi-x)^2-(\eta-y)^2}}{ct}.\]
The positive sign applies on \(S^+\), where \(\zeta>0\) and the sign is negative on \(S^-\) where \(\zeta<0\), see Figure 4.2.2.1. We have \(S=S^+\cup\overline{S^-}\).
Set \(\rho=\sqrt{(\xi-x)^2+(\eta-y)^2}\). Then it follows from (\ref{poissonhilf1})
Theorem 4.3. The solution of the Cauchy initial value problem (\ref{n2dgl})-(\ref{initial2}) is given by
\begin{eqnarray*}
v(x,y,t)&=&\frac{1}{2\pi c}\frac{\partial}{\partial t}\int_{B_{ct}(x,y)}\ \frac{f(\xi,\eta)}{\sqrt{c^2 t^2-\rho^2}}\ d\xi d\eta\\
&&+\frac{1}{2\pi c}\int_{B_{ct}(x,y)}\ \frac{g(\xi,\eta)}{\sqrt{c^2 t^2-\rho^2}}\ d\xi d\eta. \end{eqnarray*}
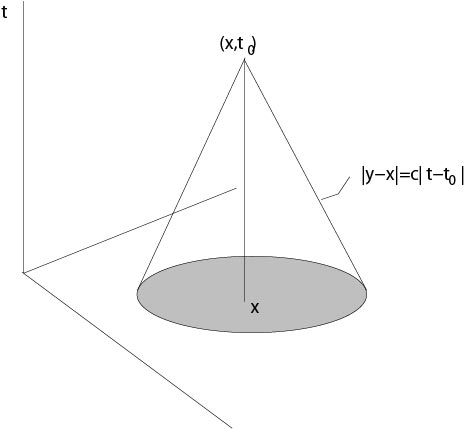
Figure 4.2.2.2: Interval of dependence, case \(n=2\)
Corollary. In contrast to the three dimensional case, the domain of dependence is here the disk \(B_{ct_o}(x_0,y_0)\) and not the boundary only. Therefore, see formula of Theorem 4.3, if \(f,\ g\) have supports in a compact domain \(D\subset\mathbb{R}^2\), then these functions have influence on the value \(v(x,y,t)\) for all time \(t>T\), \(T\) sufficiently large.
Contributors and Attributions
Integrated by Justin Marshall.


