5.4: Laplace’s Equation
( \newcommand{\kernel}{\mathrm{null}\,}\)
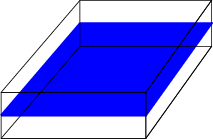
Figure 5.4.1: A conducting sheet insulated from above and below.
In a square, heat-conducting sheet, insulated from above and below
1k∂∂tu=∂2∂x2u+∂2∂y2u.
If we are looking for a steady state solution, i.e., we take u(x,y,t)=u(x,y) the time derivative does not contribute, and we get Laplace’s equation
∂2∂x2u+∂2∂y2u=0,
an example of an elliptic equation. Let us once again look at a square plate of size a×b, and impose the boundary conditions
u(x,0)=0,u(a,y)=0,u(x,b)=x,u(0,y)=0.
(This choice is made so as to be able to evaluate Fourier series easily. It is not very realistic!) We once again separate variables,
u(x,y)=X(x)Y(y),
and define
X″X=−Y″Y=−λ.
or explicitly
X″=−λX,Y″=λY.
With boundary conditions X(0)=X(a)=0, Y(0)=0. The 3rd boundary conditions remains to be implemented.
Once again distinguish three cases:
| λ>0 |
X(x)=sinαn(x), αn=nπa, λn=α2n. We find
Y(y)=Cnsinhαny+Dncoshαny=C′nexp(αny)+D′nexp(−αny).
Since Y(0)=0 we find Dn=0 (sinh(0)=0,cosh(0)=1).
| λ≤0 |
No solutions
So we have
u(x,y)=∞∑n=1bnsinαnxsinhαny
The one remaining boundary condition gives
u(x,b)=x=∞∑n=1bnsinαnxsinhαnb.
This leads to the Fourier series of x,
bnsinhαnb=2a∫a0xsinnπxadx=2anπ(−1)n+1.
So, in short, we have
V(x,y)=2aπ∞∑n=1(−1)n+1sinnπxasinhnπyansinhnπba.
The dependence on x enters through a trigonometric function, and that on y through a hyperbolic function. Yet the differential equation is symmetric under interchange of x and y. What happens?
- Answer
-
The symmetry is broken by the boundary conditions.


