1.4: Linear equations and the integrating factor
( \newcommand{\kernel}{\mathrm{null}\,}\)
One of the most important types of equations we will learn how to solve are the so-called linear equations. In fact, the majority of the course is about linear equations. In this lecture we focus on the first order linear equation. A first order equation is linear if we can put it into the form:
y′+p(x)y=f(x).
Here the word “linear” means linear in y and y′; no higher powers nor functions of y or y′ appear. The dependence on x can be more complicated.
Solutions of linear equations have nice properties. For example, the solution exists wherever p(x) and f(x) are defined, and has the same regularity (read: it is just as nice). But most importantly for us right now, there is a method for solving linear first order equations. The trick is to rewrite the left hand side of (???) as a derivative of a product of y with another function. To this end we find a function r(x) such that
r(x)y′+r(x)p(x)y=ddx[r(x)y]
This is the left hand side of (???) multiplied by r(x). So if we multiply (???) by r(x), we obtain
ddx[r(x)y]=r(x)f(x)
Now we integrate both sides. The right hand side does not depend on y and the left hand side is written as a derivative of a function. Afterwards, we solve fory. The function r(x) is called the integrating factor and the method is called the integrating factor method.
We are looking for a function r(x), such that if we differentiate it, we get the same function back multiplied by p(x). That seems like a job for the exponential function! Let
r(x)=e∫p(x)dx
We compute:
y′+p(x)y=f(x),e∫p(x)dxy′+e∫p(x)dxp(x)y=e∫p(x)dxf(x),ddx[e∫p(x)dxy]=e∫p(x)dxf(x),e∫p(x)dxy=∫e∫p(x)dxf(x)dx+C,y=e−∫p(x)dx(∫e∫p(x)dxf(x)dx+C).
Solve
y′+2xy=ex−x2,y(0)=−1
Solution
First note that p(x)=2x and f(x)=ex−x2. The integrating factor is r(x)=e∫p(x)dx=ex2. We multiply both sides of the equation by r(x) to get
ex2y′+2xex2y=ex−x2ex2,ddx[ex2y]=ex.
We integrate ex2y=ex+C,y=ex−x2+Ce−x2. Next, we solve for the initial condition −1=y(0)=1+C, so C=−2. The solution is y=ex−x2−2e−x2.
Note that we do not care which antiderivative we take when computing e∫p(x)dx. You can always add a constant of integration, but those constants will not matter in the end.
Try it! Add a constant of integration to the integral in the integrating factor and show that the solution you get in the end is the same as what we got above. An advice: Do not try to remember the formula itself, that is way too hard. It is easier to remember the process and repeat it.
Since we cannot always evaluate the integrals in closed form, it is useful to know how to write the solution in definite integral form. A definite integral is something that you can plug into a computer or a calculator. Suppose we are giveny′+p(x)y=f(x),y(x0)=y0. Look at the solution and write the integrals as definite integrals.y(x)=e∫−xx0p(s)ds(∫xx0e∫tx0p(s)dsf(t)dt+y0)You should be careful to properly use dummy variables here. If you now plug such a formula into a computer or a calculator, it will be happy to give you numerical answers.
Check that y(x0)=y0 in formula (???).
Write the solution of the following problem as a definite integral, but try to simplify as far as you can. You will not be able to find the solution in closed form.
y′+y=ex2−x,y(0)=10
Before we move on, we should note some interesting properties of linear equations. First, for the linear initial value problem y′+p(x)y=f(x), y(x0)=y0, there is always an explicit formula (???) for the solution. Second, it follows from the formula (???) that if p(x) and f(x) are continuous on some interval (a,b), then the solution y(x) exists and is differentiable on (a,b). Compare with the simple nonlinear example we have seen previously, y′=y2, and compare to Theorem 1.2.1.
Let us discuss a common simple application of linear equations. This type of problem is used often in real life. For example, linear equations are used in figuring out the concentration of chemicals in bodies of water (rivers and lakes).
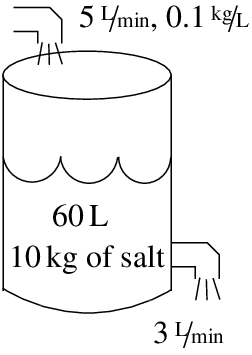
A 100 liter tank contains 10 kilograms of salt dissolved in 60 liters of water. Solution of water and salt (brine) with concentration of 0.1 kilograms per liter is flowing in at the rate of 5 liters a minute. The solution in the tank is well stirred and flows out at a rate of 3 liters a minute. How much salt is in the tank when the tank is full?
Solution
Let us come up with the equation. Let x denote the kilograms of salt in the tank, let t denote the time in minutes. For a small change Δt in time, the change in x (denoted Δx) is approximately
Δx≈(rate in x concentration in)Δt−(rate out x concentration out)Δt.
Dividing through by Δt and taking the limit Δt→0 we see that
dxdt=(rate in x concentration in)−(rate out x concentration out)
In our example, we have
rate in=5,concentration in=0.1,rate out=3,concentration out=xvolume=x60+(5−3)t.
Our equation is, therefore,
dxdt=(5 x 0.1)−(3x60+2t)
Or in the form (???)
dxdt+360+2tx=0.5
Let us solve. The integrating factor is
r(t)=exp(∫360+2tdt)=exp(32ln(60+2t))=(60+2t)3/2
We multiply both sides of the equation to get
(60+2t)3/2dxdt+(60+2t)3/2360+2tx=0.5(60+2t)3/2,ddt[(60+2t)3/2x]=0.5(60+2t)3/2,(60+2t)3/2x=∫0.5(60+2t)3/2dt+C,x=(60+2t)−3/2∫(60+2t)3/22dt+C(60+2t)−3/2,x=(60+2t)−3/2110(60+2t)5/2+C(60+2t)−3/2,x=(60+2t)10+C(60+2t)−3/2.
We need to find C. We know that at t=0, x=10. So
10=x(0)=6010+C(60)−3/2=6+C(60)−3/2
or
C=4(603/2)≈1859.03.
We are interested in x when the tank is full. So we note that the tank is full when 60+2t=100, or when t=20. So
x(20)=60+4010+C(60+40)−3/2≈10+1859.03(100)−3/2≈11.86.
See Figure 1.4.2 for the graph of x over t.
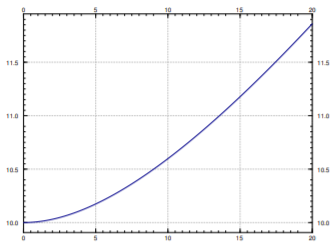
The concentration at the end is approximately 0.1186 kg/liter and we started with 16 or 0.167 kg/liter.


