9.6: The Convolution Operation
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the list of properties of the Fourier transform, we defined the convolution of two functions,
In some sense one is looking at a sum of the overlaps of one of the functions and all of the shifted versions of the other function. The German word for convolution is faltung, which means "folding" and in old texts this is referred to as the Faltung Theorem. In this section we will look into the convolution operation and its Fourier transform.
Before we get too involved with the convolution operation, it should be noted that there are really two things you need to take away from this discussion. The rest is detail. First, the convolution of two functions is a new functions as defined by
The convolution is commutative.
First, we note that the convolution is commutative:
The best way to understand the folding of the functions in the convolution is to take two functions and convolve them. The next example gives a graphical rendition followed by a direct computation of the convolution. The reader is encouraged to carry out these analyses for other functions.
Graphical Convolution of the box function and a triangle function.
Solution
In order to understand the convolution operation, we need to apply it to specific functions. We will first do this graphically for the box function
and the triangular function
as shown in Figure
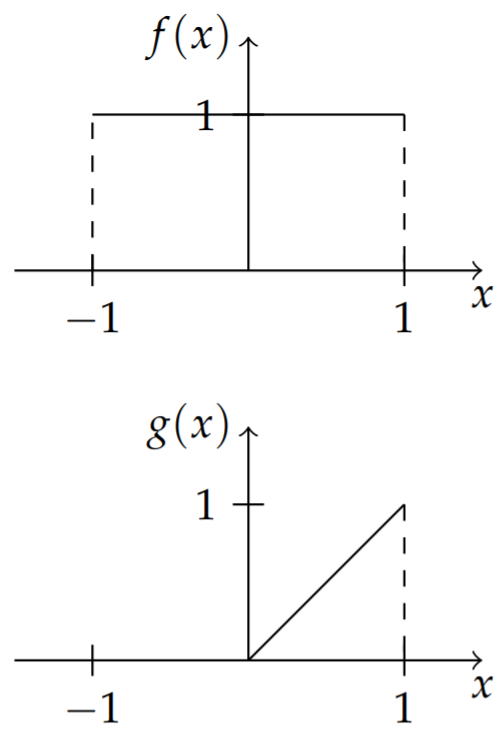
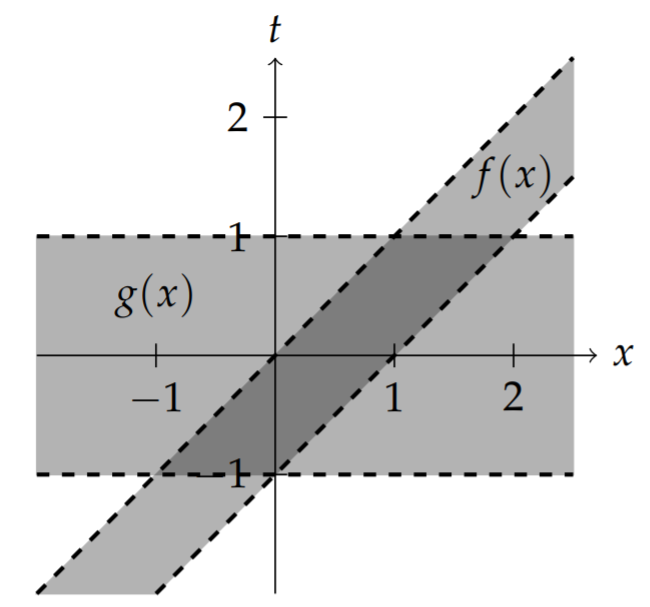
Next, we determine the contributions to the integrand. We consider the shifted and reflected function
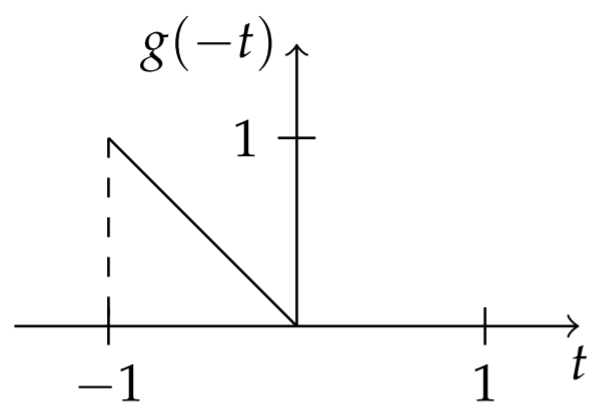
We then translate the triangle function performing horizontal shifts by
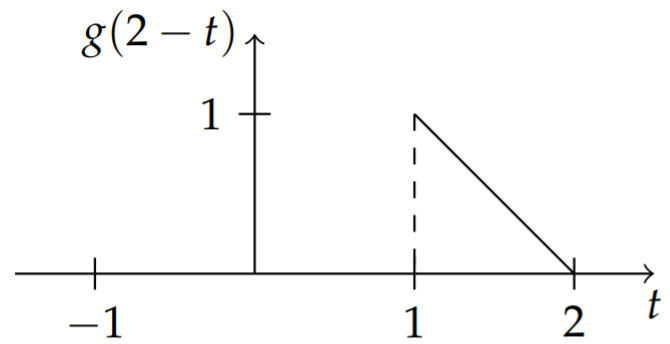
In Figure
The integrand is the product of
In the first plot of Figure
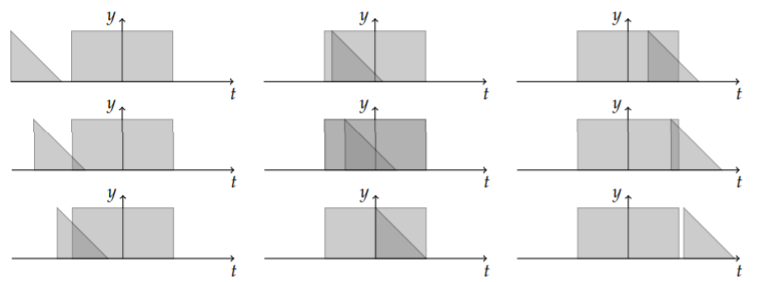
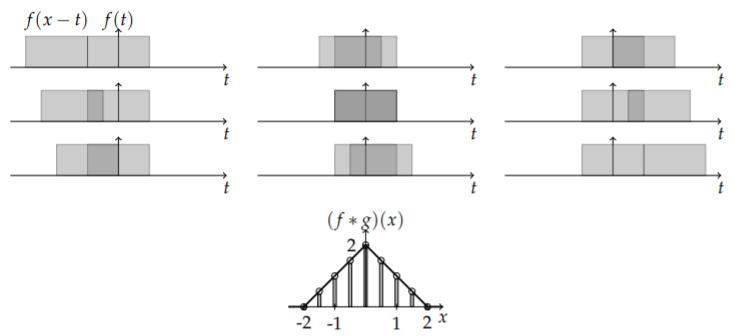
Plots of the areas of the convolution of the box and triangle functions for several values of
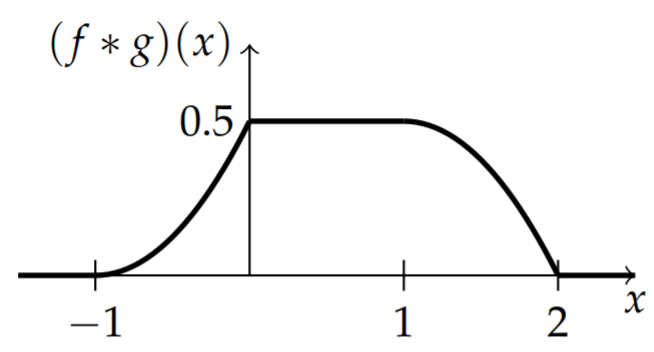
The plot of the convolution in Figure
Analytically find the convolution of the box function and the triangle function.
Solution
The nonvanishing contributions to the convolution integral are when both
Isolating the intersection in Figure
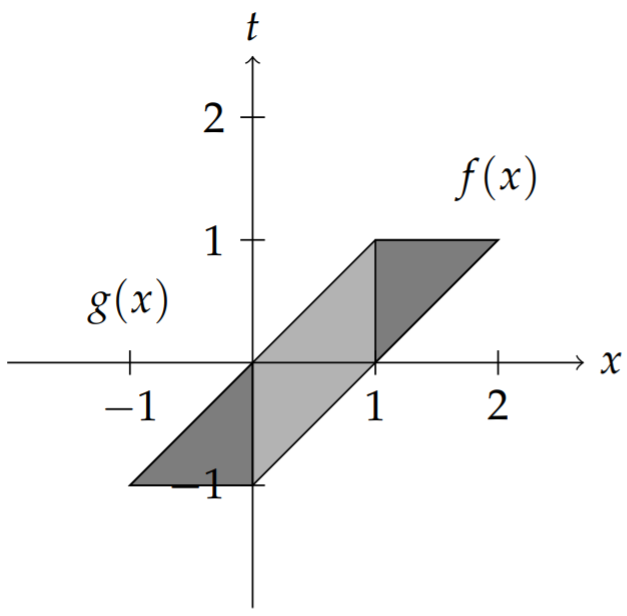
The values of the convolution can be determined through careful integration. The resulting integrals are given as
A plot of this function is shown in Figure
Convolution Theorem for Fourier Transforms
In this section we compute the Fourier transform of the convolution integral and show that the Fourier transform of the convolution is the product of the transforms of each function,
First, we use the definitions of the Fourier transform and the convolution to write the transform as
We now substitute
We see that the two integrals are just the Fourier transforms of
Compute the convolution of the box function of height one and width two with itself.
Solution
Let
For the box function, we have already found that
So, we need to compute
One way to compute this integral is to extend the computation into the complex
We can compute the above integrals if we know how to compute the integral
Then, the result can be found in terms of
We consider the integral
over the contour in Figure
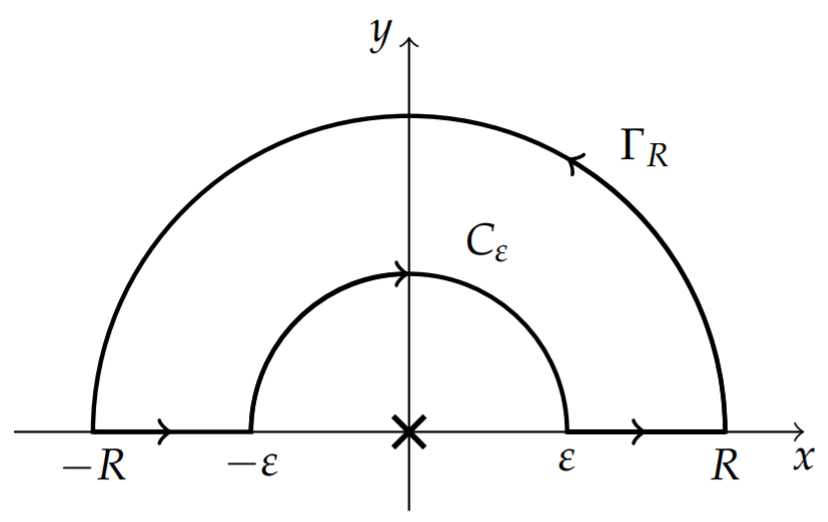
We can see that there is a double pole at
Recall from Chapter 8 that
The integral
As before, we can show that
Therefore, we find
A simple computation of the reside gives
When
We are now ready to finish the computation of the convolution. We have to combine the integrals
A plot of this solution is the triangle function,
which was shown in the last example.
Find the convolution of the box function of height one and width two with itself using a direct computation of the convolution integral.
Solution
The nonvanishing contributions to the convolution integral are when both
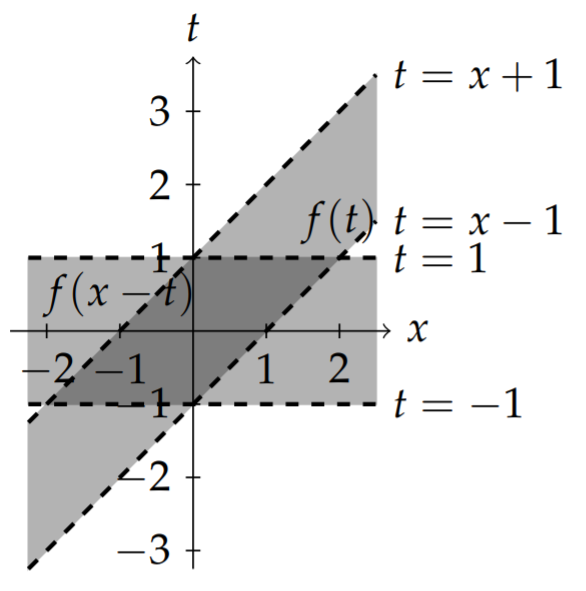
Thus, the nonzero contributions to the convolution are
Once again, we arrive at the triangle function.
In the last section we showed the graphical convolution. For completeness, we do the same for this example. In Figure
Show the graphical convolution of the box function of height one and width two with itself.
Let’s consider a slightly more complicated example, the convolution of two Gaussian functions.
Convolution of two Gaussian functions
Solution
In this example we will compute the convolution of two Gaussian functions with different widths. Let
This integral can be rewritten as
One could proceed to complete the square and finish carrying out the integration. However, we will use the Convolution Theorem to evaluate the convolution and leave the evaluation of this integral to Problem 12.
Recalling the Fourier transform of a Gaussian from Example 9.5.1, we have
and
Denoting the convolution function by
This is another Gaussian function, as seen by rewriting the Fourier transform of
In order to complete the evaluation of the convolution of these two Gaussian functions, we need to find the inverse transform of the Gaussian in Equation
Moving the constants, we then obtain
We now make the substitution
This is in the form needed to invert
Application to Signal Analysis
There are many applications of the convolution operation. One of these areas is the study of analog signals. An analog signal is a continuous signal and may contain either a finite, or continuous, set of frequencies. Fourier transforms can be used to represent such signals as a sum over the frequency content of these signals. In this section we will describe how convolutions can be used in studying signal analysis.
The first application is filtering. For a given signal there might be some noise in the signal, or some undesirable high frequencies. For example, a device used for recording an analog signal might naturally not be able to record high frequencies. Let
There are many ways to filter out unwanted frequencies. The simplest would be to just drop all of the high (angular) frequencies. For example, for some cutoff frequency
as shown in Figure
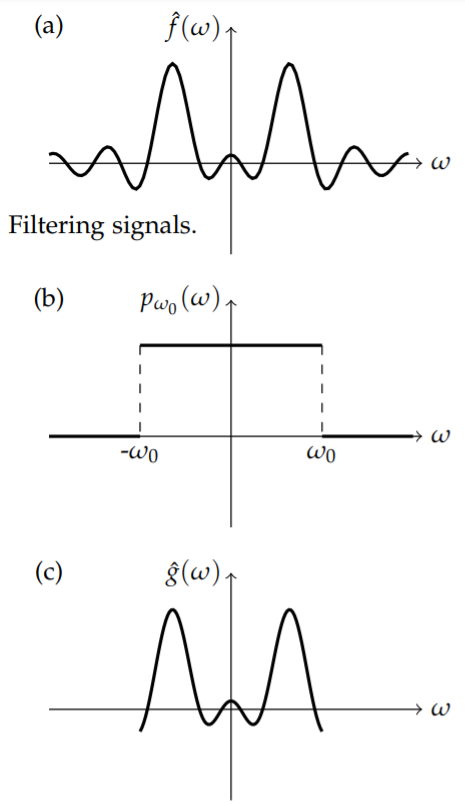
In general, we multiply the Fourier transform of the signal by some filtering function
The new signal,
Such processes occur often in systems theory as well. One thinks of
Another application of the convolution is in windowing. This represents what happens when one measures a real signal. Real signals cannot be recorded for all values of time. Instead data is collected over a finite time interval. If the length of time the data is collected is
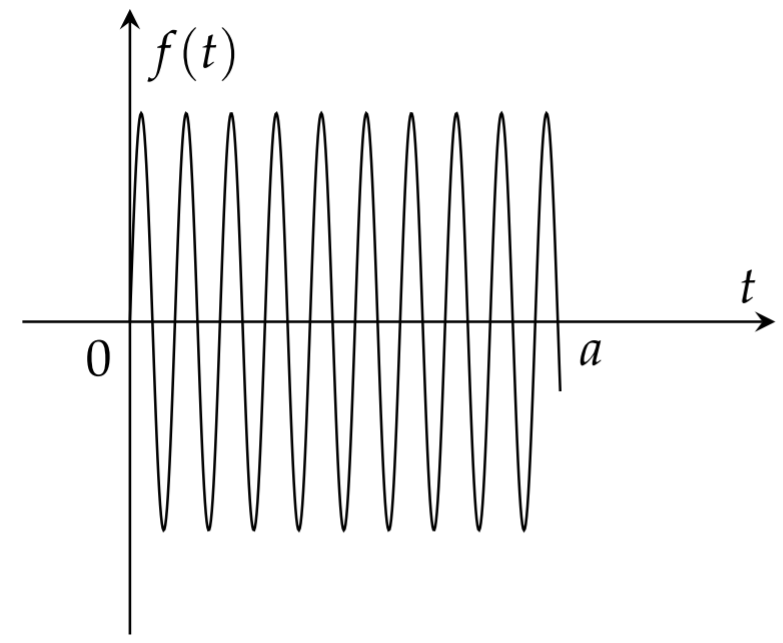
We return to the finite wave train in Example 9.5.6 given by
Solution
We can view this as a windowed version of
This is shown in Figure
Note that the convolution in frequency space requires the extra factor of
The convolution in spectral space is defined with an extra factor of
We need the Fourier transforms of
The Fourier transform of the cosine function,
Note that we had earlier computed the inverse Fourier transform of this function in Example 9.5.5.
Inserting these results in the convolution integral, we have
This is the same result we had obtained in Example 9.5.6.
Parseval’s Equality
The integral/sum of the (modulus) square of a function is the integral/sum of the (modulus) square of the transform.
As another example of the convolution theorem, we derive Parseval’s Equality (named after Marc-Antoine Parseval (1755-1836)):
This equality has a physical meaning for signals. The integral on the left side is a measure of the energy content of the signal in the time domain. The right side provides a measure of the energy content of the transform of the signal. Parseval’s equality, is simply a statement that the energy is invariant under the Fourier transform. Parseval’s equality is a special case of Plancherel’s formula (named after Michel Plancherel, 1885-1967).
Let’s rewrite the Convolution Theorem in its inverse form
Then, by the definition of the inverse Fourier transform, we have
Setting
Now, let
So, inserting this result into Equation
which yields Parseval’s Equality in the form
As noted above, the forms in Equations
In general, there is a Parseval identity for functions that can be expanded in a complete sets of orthonormal functions,
Here


