6.1: Problem Set

Last updated
Save as PDF

Page ID: 24166

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

EXERCISE $\PageIndex{1}$

Consider the $C^{r}$, $r \ge 1$, autonomous vector field on $\mathbb{R}^2$:

$\dot{x} = f(x)$,

with flow

$\phi_{t}(\cdot)$,

and let $x = \bar{x}$ denote a hyperbolic saddle type equilibrium point for this vector field. We denote the local stable and unstable manifolds of this equilibrium point by:

$W_{loc}^{s}(\bar{x})$, $W_{loc}^{u}(\bar{x})$,

respectively. The global stable and unstable manifolds of $\bar{x}$ are defined by:

$W^{s}(\bar{x}) \equiv \cup_{t \le 0} \phi_{t} (W_{loc}^{s}(\bar{x}))$,

$W^{u}(\bar{x}) \equiv \cup_{t \ge 0} \phi_{t} (W_{loc}^{s}(\bar{x}))$,

(a) Show that $W^{s}(\bar{x})$ and $W^{u}(\bar{x})$ are invariant set.

(b) Suppose that $p \in W^{s}(\bar{x})$, show that $\phi_{t}(p) \rightarrow \bar{x}$ at an exponential rate as $t \rightarrow \infty$.

(c) Suppose that $p \in W^{u}(\bar{x})$, show that $\phi_{t}(p) \rightarrow \bar{x}$ at an exponential rate as $t \rightarrow -\infty$.

EXERCISE $\PageIndex{2}$

Consider the $C^{r}, r \ge 1$, autonomous vector field on $\mathbb{R}^2$ having a hyperbolic saddle point. Can its stable and unstable manifolds intersect at an isolated point (which is not a fixed point of the vector field) as shown in figure 2?

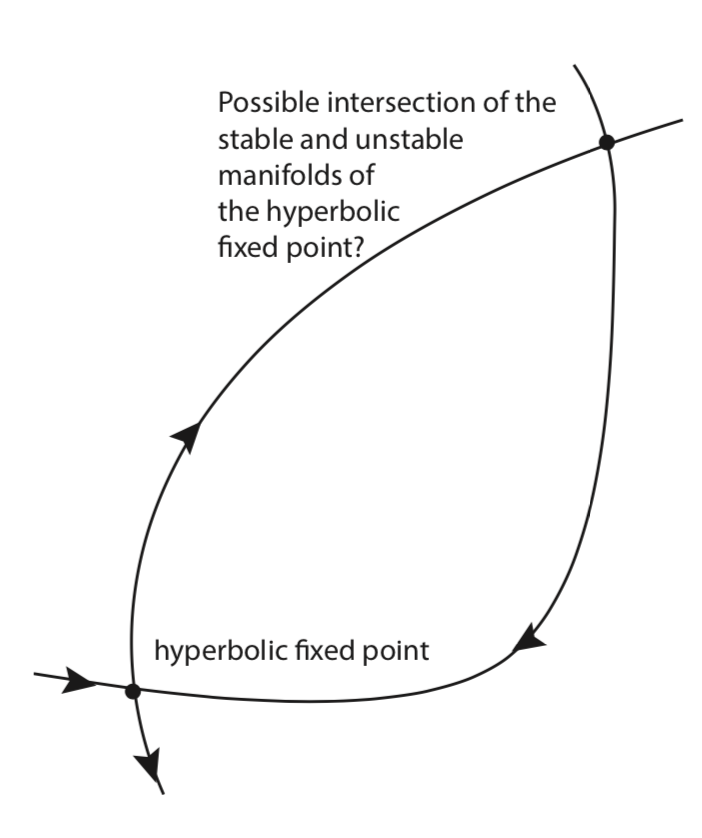
$Screen Shot 2019-09-26 at 12.45.53 PM.png$

EXERCISE $\PageIndex{3}$

Consider the following autonomous vector field on the plane:

$\dot{x} = \alpha x$,

\[\dot{y} = \beta y + \gamma x^{n+1}, \label{6.42}\]

where $\alpha < 0$, $\beta > 0$, $\gamma$ is a real number, and n is a positive integer.

Show that the origin is a hyperbolic saddle point.
Compute and sketch the stable and unstable subspaces of the origin.
Show that the stable and unstable subspaces are invariant under the linearized dynamics.
Show the the flow generated by this vector field is given by:
$x(t, x_{0}) = x_{0}e^{\alpha t}$,

$y(t, x_{0}, y_{0}) = e^{\beta t}(y_{0} - \frac{\gamma x_{0}^{n+1}}{\alpha (n+1) - \beta}) + (\frac{\gamma x_{0}^{n+1}}{\alpha (n+1) - \beta}) e^{\alpha (n+1)t}$
Compute the global stable and unstable manifolds of the origin from the flow.
Show that the global stable and unstable manifolds that you have computed are invariant.
Sketch the global stable and unstable manifolds and discuss how they depend on g and n.

EXERCISE $\PageIndex{4}$

Suppose $\dot{x} = f(x), x \in \mathbb{R}^n$ is a $C^r$ vector field having a hyperbolic fixed point, $x = x_{0}$, with a homoclinic orbit. Describe the homoclinic orbit in terms of the stable and unstable manifolds of $x_{0}$.

EXERCISE $\PageIndex{5}$

Suppose $\dot{x} = f(x), x \in \mathbb{R}^n$ is a $C^r$ vector field having hyperbolic fixed points, $x = x_{0}$ and $x_{1}$, with a heteroclinic orbit connecting $x_{0}$ and $x_{1}$. Describe the heteroclinic orbit in terms of the stable and unstable manifolds of $x_{0}$ and $x_{1}$.