3.3: Concurrent

Last updated
Save as PDF

Page ID: 89849

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Definition: Median

A line is a median if and only if it connects a vertex of a triangle to the midpoint of the opposing side.

3.3.1 Explore

Geogebra will be helpful for performing these experiments. Be as detailed as you can with your conjectures.

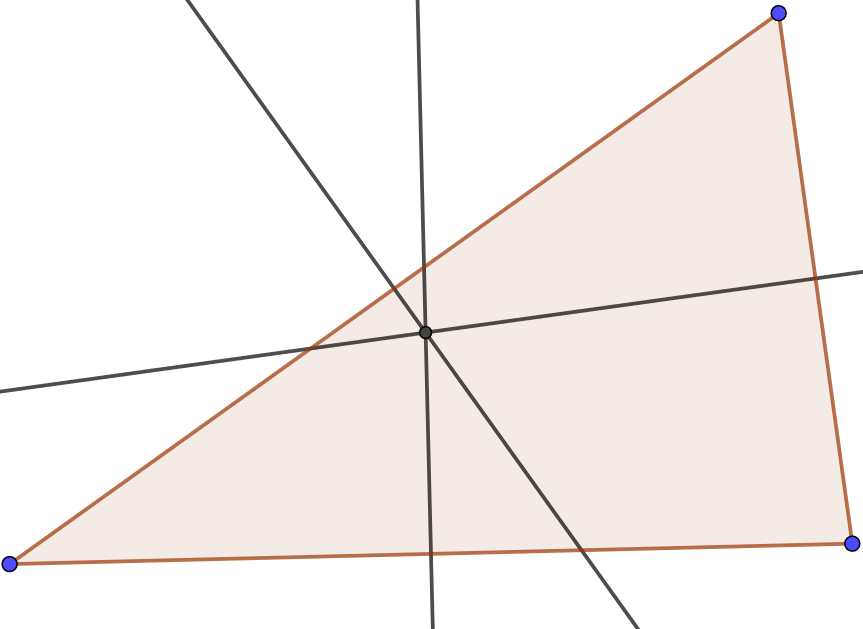
Use the Geogebra example in \(\PageIndex{1}\) to experiment with the relationship of the three perpendicular bisectors of a triangle. Move the vertices of the triangle around. What remains true about the perpendicular bisectors?

3.3.1.jpg — Figure \(\PageIndex{1}\): GeoGebra: Perpendicular Bisectors

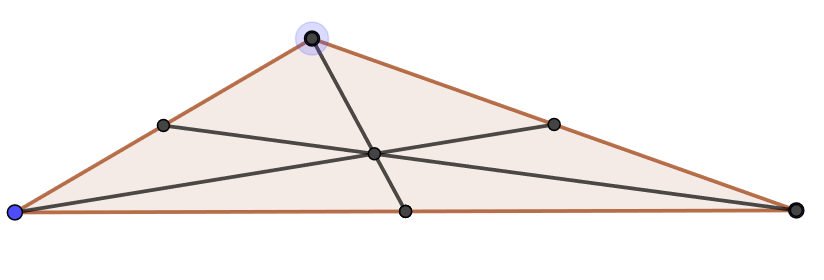
Use the Geogebra example in \(\PageIndex{2}\) to experiment with the relationship of the three medians of a triangle. Move the vertices of the triangle around. What remains true about the medians?

3.3.2.png — Figure \(\PageIndex{2}\): GeoGebra: Medians

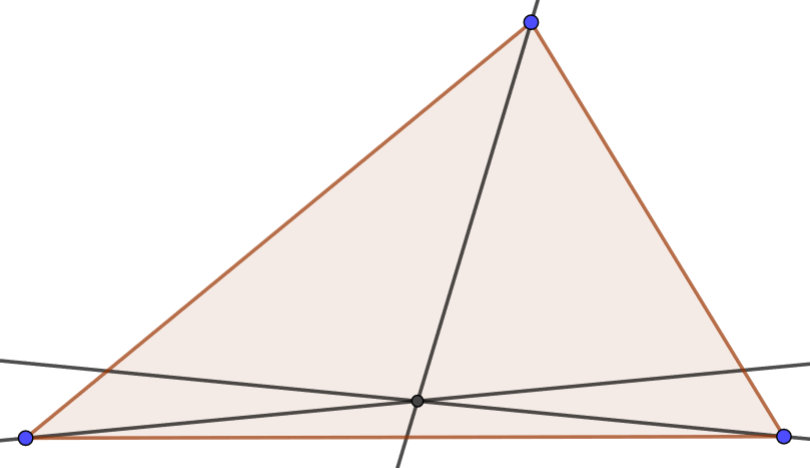
Use the Geogebra example in \(\PageIndex{3}\) to experiment with the relationship of the three angle bisectors of a triangle. Move the vertices of the triangle around. What remains true about the angle bisectors?

3.3.3.jpg — Figure \(\PageIndex{3}\): GeoGebra: Angle Bisectors

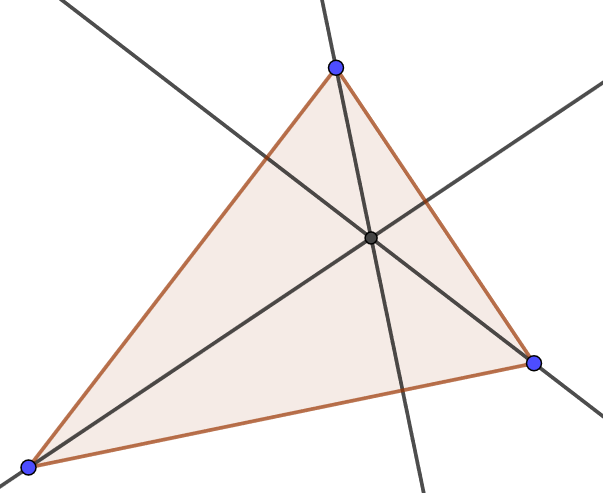
Use the Geogebra example in \(\PageIndex{4}\) to experiment with the relationship of the three altitudes of a triangle. Move the vertices of the triangle around. What remains true about the altitudes?

3.3.4.png — Figure \(\PageIndex{4}\): GeoGebra: Altitudes

Construct △ABC. Construct △XYZ such that X-B-Y, Y-C-Z, Z-A-X and XY ll AC, YZ ll AB, ZX ll BC. Construct the perpendicular bisectors of △XYZ. What appears to be true of these with respect to △ABC.

3.3.2 Prove

Lemma

Consider three points A, B, C with ℓ₁ and ℓ₂ the perpendicular bisectors of AB and BC respectively. Let M₂ = ℓ₂ ∩ BC. Show ℓ₁ ll ℓ₂ implies the existence of D = ℓ₂ ∩ AB such that A, B and D are collinear and ∠BDM₂ is a right angle.

Theorem: Perpendicular bisectors

Prove the conjecture about the perpendicular bisectors.

Theorem: Circumcenter

Three points uniquely determine a circle.

Lemma

Two medians intersect at a point 2/3 of the way down both medians.

Theorem: Medians

Prove the conjecture about the medians.

Theorem

A point is on the angle bisector of an angle if and only if it is equidistant from both sides of the angle.

Theorem: Angle bisectors

Prove the conjecture about the angle bisectors.

Theorem：Incenter

For each triangle there exists a circle inside and tangent to all three sides.

Theorem： Altitudes

Prove the conjecture about the altitudes.