Skip to main content
Mathematics LibreTexts

4.4: Symmetries

  1. Last updated
  2. Save as PDF
  • Page ID
    89855

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    4.4.1 Explore Symmetries

    Definition: Symmetry

    A set of points A has symmetry of type T for some transformation T if and only if T(A) = A.

    Confirm T(x, y) = (-y, x) is a symmetry of the set {(1, 1), (-1, 1), (-1, -1), (1, -1)}.

    Demonstrate T(x, y) = (-y, x) is not a symmetry of the set {(0, 0), (1, 0), (1, 1), (0, 1)}.

    What points do you have to add to {(1, 1), (-1, 1), (-1, -1), (1, -1), (1, 0)} so T(x, y) = (-y, x) is a symmetry of this set?

    List all symmetries of a square by labeling the vertices and giving the type and parameters for the transformations.

    List all symmetries of a regular n-sided polygon (n-gon) by labeling the vertices and giving the type and parameters for the transformations.

    For one of the regular n-gons check the following.

    1. What is the composition of two rotational symmetries?
    2. What is the composition of two reflection symmetries?
    3. What is the smallest number of symmetries you can use to generate all the symmetries?

    Draw some regular n-gon. Color in the n-gon so that the colored figure maintains the rotational symmetries, but not the reflectional symmetries.

    Draw some regular n-gon. Color in the n-gon so that the colored figure maintains the reflectional symmetries, but not the rotational symmetries.

    Draw a figure that has translational symmetry.

    Draw a figure that has translational symmetry and exactly one reflectional symmetry.

    Draw a figure that has translational symmetry and rotational symmetry.

    Draw a figure that has dilational symmetry.

    4.4.2 Explore Tesselations

    Definition: Tesselation

    A covering of the plane is a tesselation if and only if it consists of a single shape infinitely reproduced using a finite set of transformations.

    Definition: Tiling

    A covering of the plane is a tiling if and only if it consists of a finite set of shapes infinitely reproduced using a finite set of transformations.

    Analyze the tesselation as follows.

    1. Identify the generating shape.
    2. Identify the smallest set of transformations that can generate the tesselation.
    3. List all symmetries of the tesselation.
    4. Identify the smallest set of symmetries of the tesselation that can generate all the symmetries of the tesselation.
    Definition: Conway Label

    The following labeling of tesselations derives from the book The Symmetries of Things by John Conway, Heidi Burgiel, and Chaim Goodman-Strauss. Follow these steps in order to identify and label the type of symmetry group of a tesselation. The resulting notation is called the signature

    1. Identify all lines of reflection.
    2. If two or more lines of reflection intersect in a point, write *n1n2... where n1, n2 are the number of lines intersecting at each unique point of intersection.
    3. If any line of reflection does not intersect other lines of reflection, just write one * for each of these.
    4. Identify any rotations that are not the composition of reflections already listed.
    5. Write n1n2... in front of any * for each rotation where n1, n2 are the order of the rotations.
    6. Identify any glide reflections that are not the composition of reflections or rotations already listed.
    7. Write × at the end of the signature for each of these glide reflections.
    8. Identify any translations that are not the composition of other symmetries already listed.
    9. Write ○ at the front of the signature for each pair of these translations.

    See the example signatures in Figures \(\PageIndex{1}\) to \(\PageIndex{4}\).

    Find the signatures of two tesselations from the class archive at here. You may not choose two with the same signature.

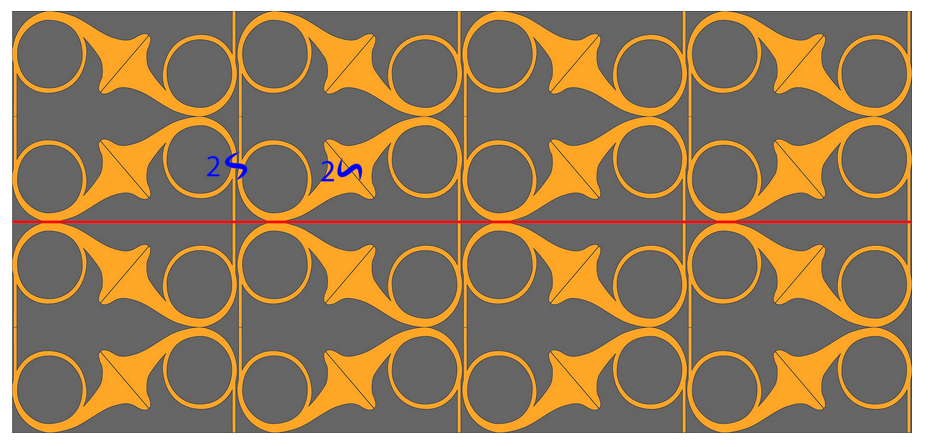
    Find the signature of the tesselation in Figure \(\PageIndex{1}\).

    Begin the tesselation project.

    4.4.3 Tesselation Images

    4.4.1.png
    Figure \(\PageIndex{1}\): Tesselation
    4.4.2.png
    Figure \(\PageIndex{2}\): Signature *236 (Variation on a Theme by Scott Roseman)
    4.4.3.png
    Figure \(\PageIndex{3}\): Signature 22*
    4.4.4.png
    Figure \(\PageIndex{4}\): Signature *X

    This page titled 4.4: Symmetries is shared under a GNU Free Documentation License 1.3 license and was authored, remixed, and/or curated by Mark A. Fitch via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.