4.3: Isoseles Triangles
- Page ID
- 23600
A triangle with two equal sides is called isosceles; the remaining side is called the base.
Assume \(\triangle ABC\) is an isosceles triangle with the base \([AB]\). Then
\(\measuredangle ABC \equiv - \measuredangle BAC.\)
Moreover, the converse holds if \(\triangle ABC\) is nondegenerate.
The following proof is due to Pappus of Alexandria.
- Proof
-
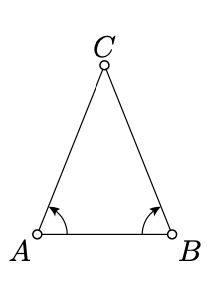
Note that
\(CA = CB\), \(CB = CA\), \(\measuredangle ACB \equiv -\measuredangle BCA\).
By Axiom IV,
\(\triangle CAB \cong \triangle CBA.\)
Applying the theorem on the signs of angles of triangles (Theorem 3.3.1) And Axiom IV again, we get that
\(\measuredangle BAC \equiv -\measuredangle ABC.\)
To prove the converse, we assume that \(\measuredangle CAB \equiv - \measuredangle CBA\). By ASA condition (Theorem 4.2.1), \(\triangle CAB \cong \triangle CBA\). Therefore, \(CA = CB\).
A triangle with three equal sides is called equilateral.
Exercise \(\PageIndex{1}\)
Let \(\triangle ABC\) be an equilateral triangle. Show that
\(\measuredangle ABC = \measuredangle BCA = \measuredangle CAB.\)
- Hint
-
Apply Theorem 4.3.1 twice


