4.4: Side-Side-Side condition
- Page ID
- 23601
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)\(\triangle ABC \cong \triangle A'B'C'\) if
\(A'B' = AB\), \(B'C' = BC\) and \(C'A' = CA\).
Note that this condition is valid for degenerate triangles as well.
- Proof
-
Choose \(C''\) so that \(A'C'' = A'C'\) and \(\measuredangle B'A'C'' = \measuredangle BAC\). According to Axiom IV,
\(\triangle A'B'C'' \cong \triangle ABC.\)
It will suffice to prove that
\[\triangle A'B'C' \cong \triangle A'B'C''.\]
The condition 4.4.1 trivially holds if \(C'' = C'\). Thus, it remains to consider the case \(C'' \ne C'\).
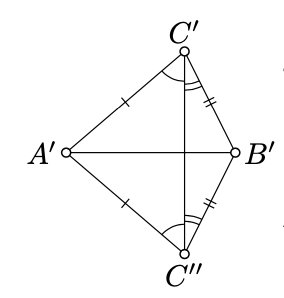
Clearly, the corresponding sides of \(\triangle A'B'C'\) and \(\triangle A'B'C''\) are equal. Hence the triangles \(\trianggle C'A'C''\) and \(\triangle C'B'C''\) are isosceles. By Theorem 4.3.1, we have
\(\begin{array} {l} {\measuredangle A'C''C' \equiv -\measuredangle A'C'C''} \\ {\measuredangle C'C''B' \equiv -\measuredangle C''C'B'.} \end{array}\)
Adding them, we get
\(\measuredangle A'C''B' \equiv -\measuredangle A'C'B'.\)
Applying Axiom IV again, we get 4.4.1
If \(AB + BC = AC\), then \(B \in [AC]\).
- Proof
-
We may assume that \(AB > 0\) and \(BC > 0\); otherwise \(A = B\) or \(B = C\).
Arguing by contradiction, suppose \(AB + BC = AC\). Choose \(B' \in [AC]\) such that \(AB = AB'\); note that \(BC = B'C\) and \(\measuredangle AB'C = \pi\).
By \(SSS\),
\(\triangle ABC \cong \triangle AB'C.\)
Therefore \(\measuredangle ABC = \pi\). By Theorem 2.4.1, \(B\) lies between \(A\) and \(C\).
Let \(M\) be the midpoint of the side \([AB]\) of \(\triangle ABC\) and \(M'\) be the midpoint of the side \([A'B']\) of \(\triangle A'B'C'\). Assume \(C'A' = CA\), \(C'B' = CB\), and \(C'M' = CM\). Prove that
\(\triangle A'B'C' \cong \triangle ABC\).
- Hint
-
Consider the points \(D\) and \(D'\), such that \(M\) is the midpoint of \([CD]\) and \(M'\) is the midpoint of \([C'D']\). Show that \(\triangle BCD \cong \triangle B'C'D'\) and use it to prove that \(\triangle A'B'C' \cong \triangle ABC\).
Let \(\triangle ABC\) be an isosceles triangle with the base \([AB]\). Suppose that \(CA' = CB'\) for some points \(A' \in [BC]\) and \(B' \in [AC]\). Show that
(a) \(\triangle AA'C \cong \triangle BB'C\);
(b) \(\triangle ABB' \cong \triangle BAA'\).
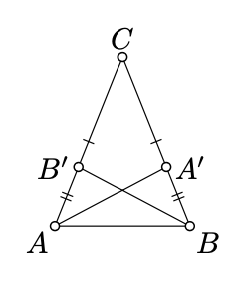
- Hint
-
(a) Apply SAS.
(b) Use (a) and apply SSS.
Let \(\triangle ABC\) be a nondegenerate triangle and let \(f\) be a motion of the plane such that
\(f(A) = A\), \(f(B) = B\) and \(f(C) = C\).
Show that \(f\) is the identity map; that is, \(f(X) = X\) for any point \(X\) on the plane.
- Hint
-
Without loss of generally, we may assume that \(X\) is distinct from \(A, B,\) and \(C\). Set \(f(X) = X'\); assume \(X' \ne X\).
Note that \(AX = AX'\), \(BX = BX'\), and \(CX = CX'\). By SSS we get that \(\angle ABX = \pm \measuredangle ABX'\). Since \(X \ne X'\), we get that \(\measuredangle ABX \equiv - \measuredangle ABX'\). The same way we get that \(\measuredangle CBX \equiv -\measuredangle CBX'\). Subtracting these two identities from each other, we get that \(\measuredangle ABC \equiv - \measuredangle ABC\). Conclude that \(\measuredangle ABC = 0\) or \(\pi\). That is, \(\triangle ABC\) is degenerate -- a contradiction.