2.6: The SSS Theorem

Last updated
Save as PDF

Page ID: 34129

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

We now consider the case where the side of two triangles are known to be of the same length.

Theorem $\PageIndex{1}$: Side-Side-Side (SSS) Theorem

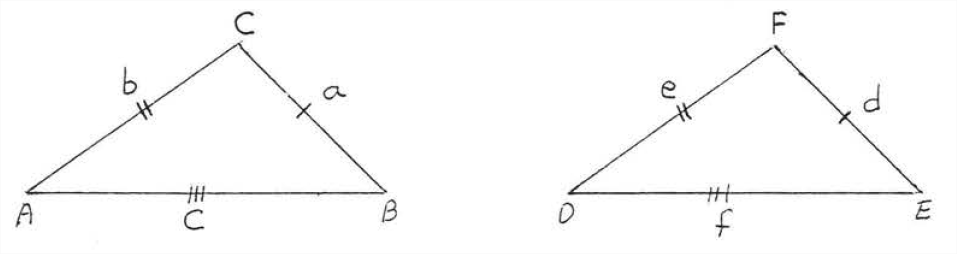
Two triangles are congruent if three sides of one are equal respectively to three sides of the other ($SSS = SSS$).

Theorem $\PageIndex{1}$ is demonstrated in Figure $\PageIndex{1}$: if $a=d, b=e,$ and $c=f$ then $\triangle ABC \cong \triangle DEF$

Figure $\PageIndex{1}$: $\triangle ABC \cong \triangle DEF$ because $SSS = SSS$.

Example $\PageIndex{1}$

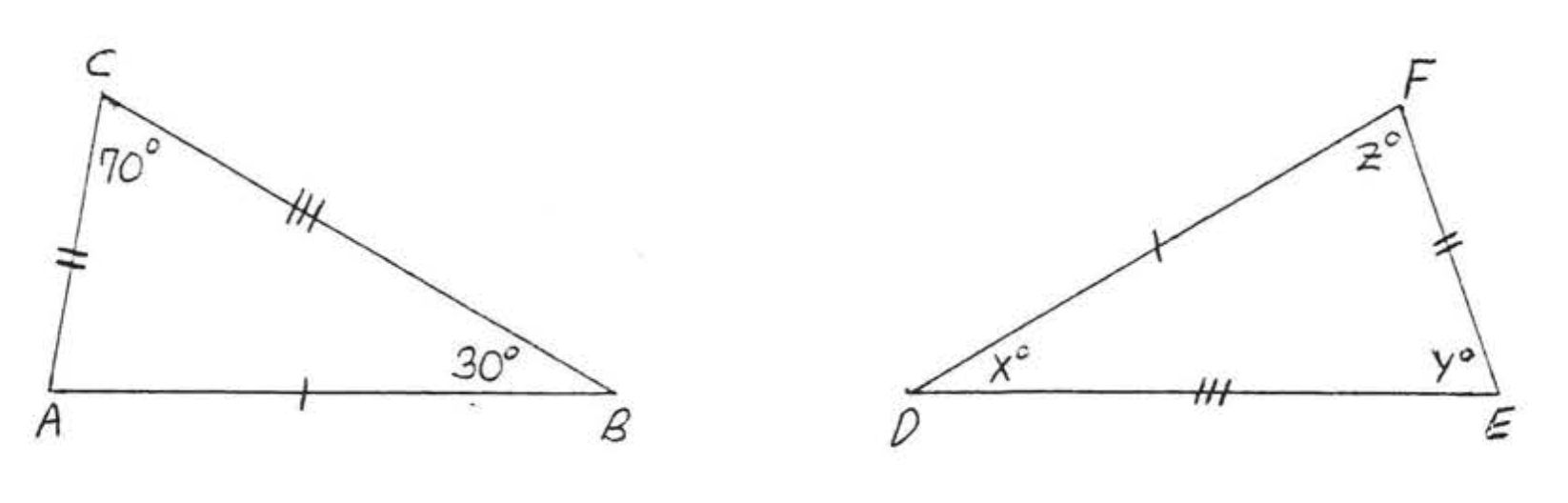
Find $x, y, z:$

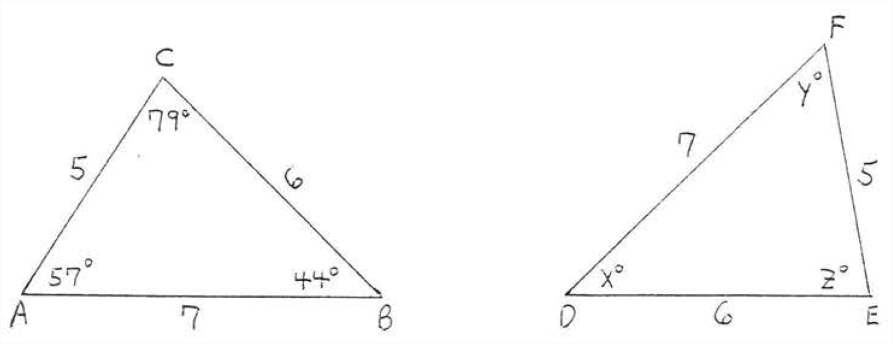
$clipboard_e89a56f3010d2114e1c007fecb808f43e.png$

Solution

$AB = 7 = DF$. Therefore $\angle C,$ the angle opposite AB must correspond to $\angle E$, the angle opposite $DF$. In the same way $\angle A$ corresponds to $\angle F$ and $\angle B$ corresponds to $\angle D$. We have $\triangle ABC \cong \triangle FDE$ by $SSS = SSS$, so

$x^{\circ}=\angle D=\angle B=44^{\circ}$

$y^{\circ}=\angle F=\angle A=57^{\circ}$

$z^{\circ}=\angle E=\angle C=79^{\circ}$

Answer: $x = 44, y=57, z=79$

Proof of Theorem $\PageIndex{1}$

In Figure $\PageIndex{1}$, place $\triangle ABC$ and $\triangle DEF$ so that their longest sides coincide, in this case $AB$ and $DE$. This can be done because $AB = c= r = DE.$ Now draw $CF$, forming angles $1,2,3,$ and 4 (Figure $\PageIndex{2}$). The rest of the proof will be presented in double-column form:

Figure $\PageIndex{2}$: Place $\triangle ABC$ and $\triangle DEF$ so that $AB$ and DE coincide and draw $CF$.

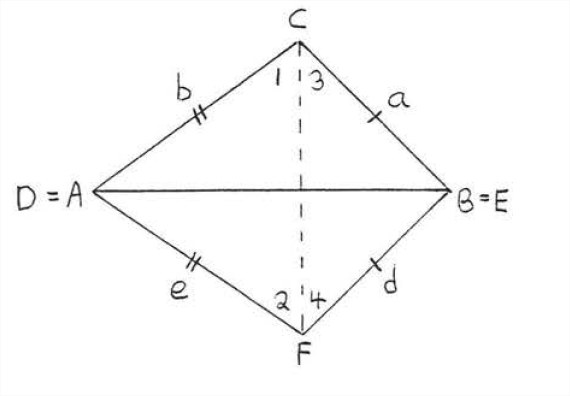
Statement	Reasons
1. $\angle 1 = \angle 2$.	1. The base angles of isosceles triangle $CAF$ are equal (Theorem $\PageIndex{1}$, section 2.5).
2. $\angle 3 = \angle 4$.	2. The base angles of isosceles triangle $CBF$ are equal.
3. $\angle C = \angle F$.	3. $\angle C = \angle 1 + \angle 3 = \angle 2 + \angle 4 = \angle F$.
4. $AC = DF$.	4. Given, $AC = b = e = DF$.
5. $BC = EF$.	5. Given, $BC = a = d = EF$.
6. $\triangle ABC \cong \triangle DEF$.	6. $SAS = SAS$: $AC, \angle C, BC$ of $\triangle ABC = DF$, $\angle F$, $EF$ of $\triangle DEF$.

Example $\PageIndex{2}$

Given $AB = DE, BC = EF,$ and $AC = DF$. Prove $\angle C = \angle F$

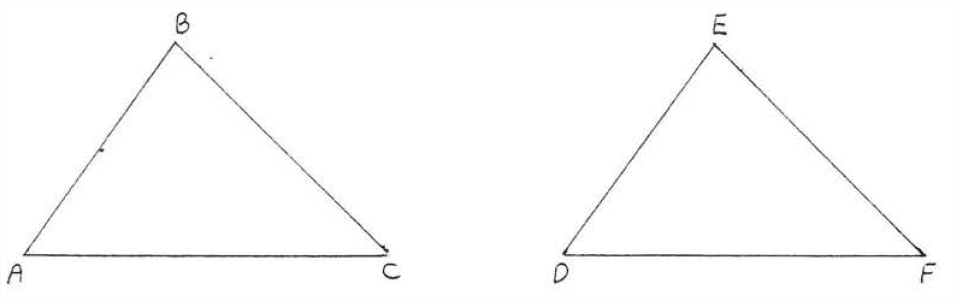
$clipboard_ee0c0f0d6ef166db1034093a3a6e507fe.png$

Solution

Statements	Reasons
1. $AB = DE$.	1. Given.
2. $BC = EF$.	2. Given.
3. $AC = DF$.	3. Given.
4. $\triangle ABC \cong \triangle DEF$.	4. $SSS = SSS$: $AB, BC, AC$ of $\triangle ABC = DE$, $EF, DF$ of $\triangle DEF$.
5. $\angle C = \angle F$.	5. Corresponding angles of congruent triangles are equal.

Application: Triangular Bracing

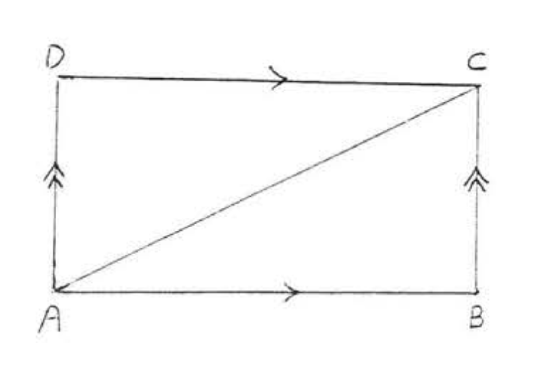
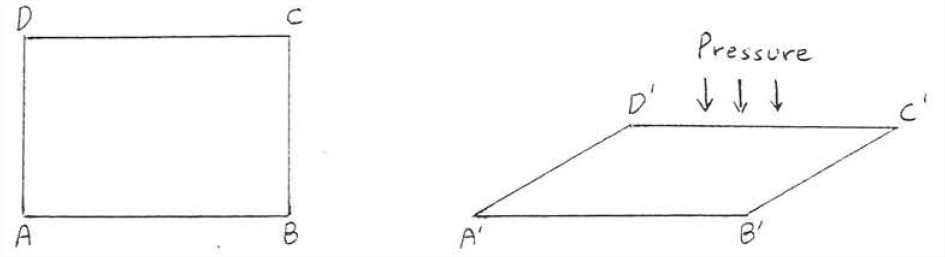
The SSS Theorem is the basis of an important principle of construction engineering called triangular bracing. Imagine the line segments in Figure $\PageIndex{3}$ to be beans of wood or steel joined at the endpoints by nails or screws. If pressure is applied to one of the sides, $ABCD$ will collapse and look like $A'B'C'D'$.

Figure $\PageIndex{3}$: $ABCD$ collapses into $A'B'C'D'$, when pressure is applied.

Now suppose points $A$ and $C$ are joined by a new beam, called a brace (Figure $\PageIndex{4}$). The structure will not collapse as long as the beans remain unbroken and joined together. It is impossible to deform $ABCD$ into any other shape $A'B'C'D'$ because if $AB = A'B'$, $BC = B'C'$, and $AC = A'C'$ then $\triangle ABC$ would be congruent to $\triangle A'B'C'$ by $SSS = SSS$.

Figure $\PageIndex{4}$: $ABCD$ cannot collapse into $A'B'C'D'$ as long as the beams remain unbroken and Jotned together.

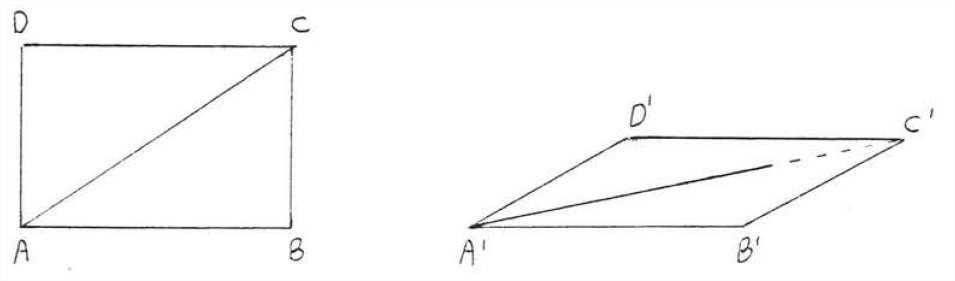
We sometimes say that a triangle is a rigid figure; once the sides of a triangle are fixed the angles cannot be changed. Thus in Figure $\PageIndex{4}$, the shape of $\triangle ABC$ cannot be changed as long as the lengths of its sides remain the same.

Problems

1 - 8. For each of the following (1) write the congruence statement,

(2) given the reason for (1) ($SAS$, $ASA$, $AAS$, or $SSS$ Theorem), and

(3) find $x$, or $x$ and $y$, or $x, y$, and $z$.

$Screen Shot 2020-11-02 at 5.19.40 PM.png$

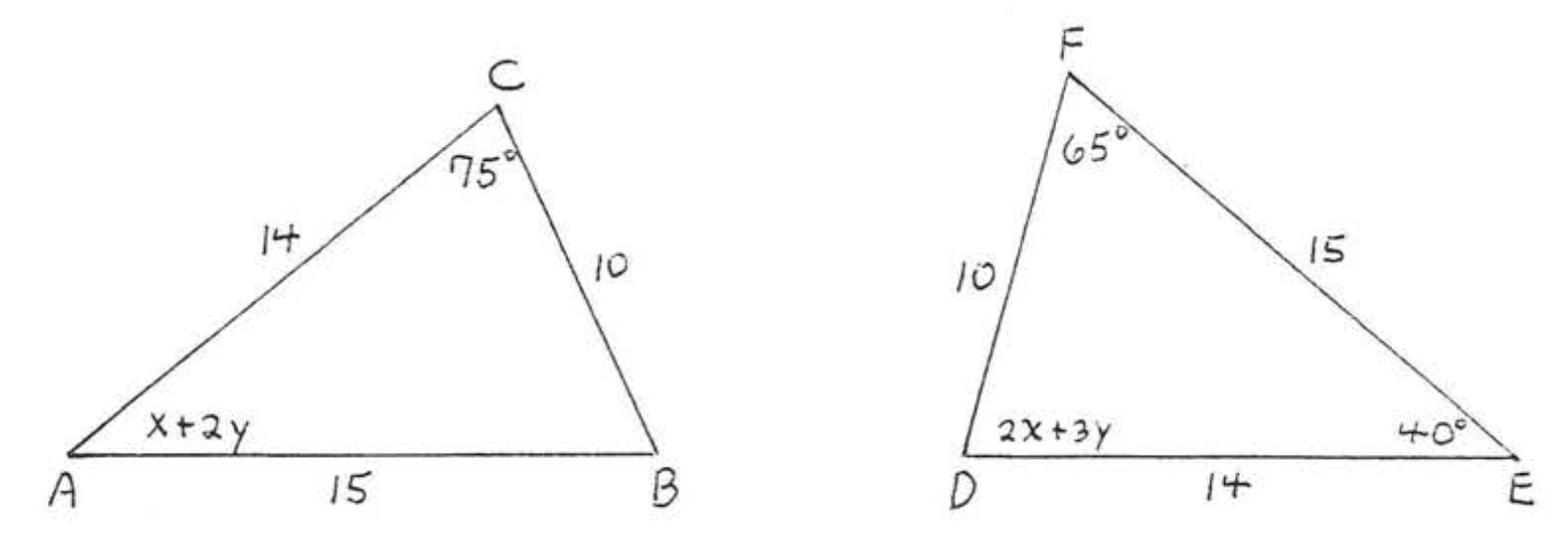
$Screen Shot 2020-11-02 at 5.20.08 PM.png$

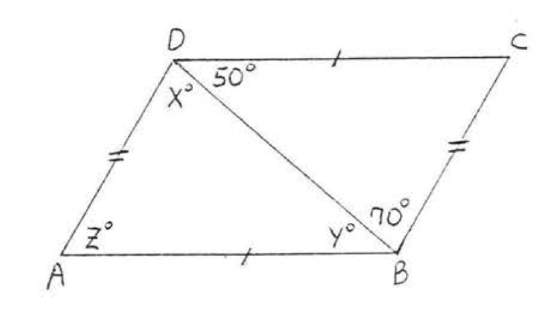
$Screen Shot 2020-11-02 at 5.20.26 PM.png$

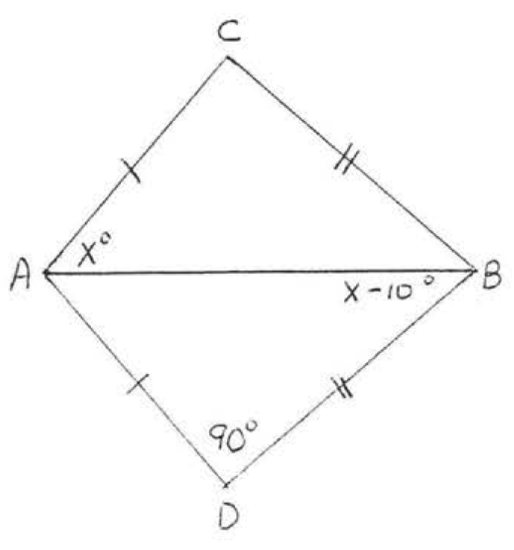
$Screen Shot 2020-11-02 at 5.28.04 PM.png$

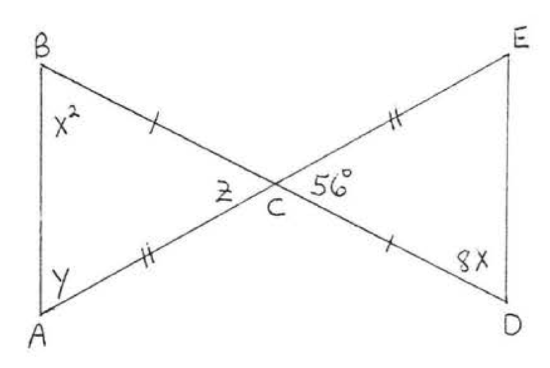
$Screen Shot 2020-11-02 at 5.28.23 PM.png$

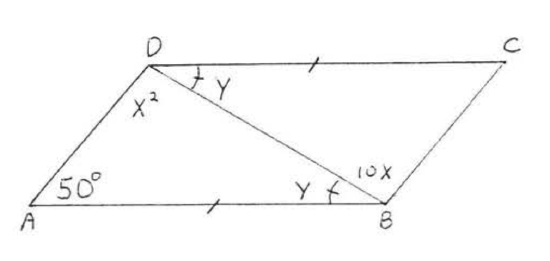
$Screen Shot 2020-11-02 at 5.28.39 PM.png$

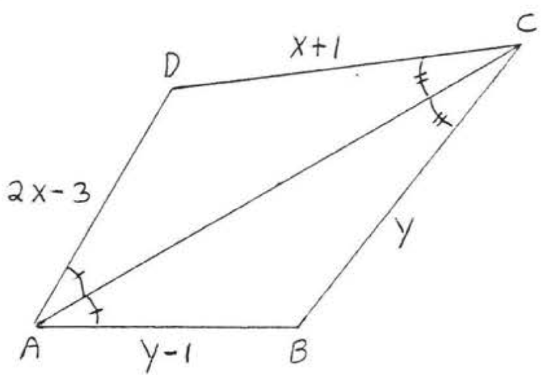
$Screen Shot 2020-11-02 at 5.29.05 PM.png$

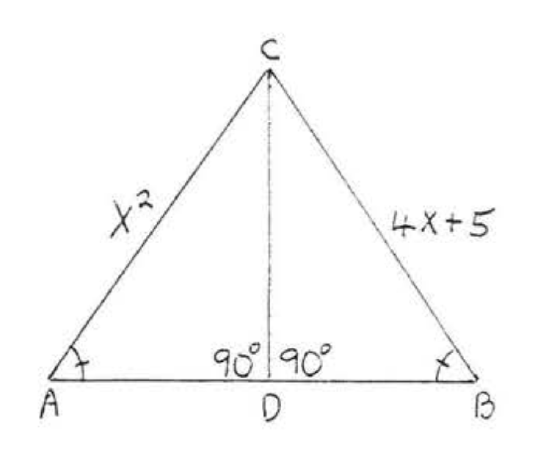
$Screen Shot 2020-11-02 at 5.29.18 PM.png$

9. Given $AB = DE$, $BC = EF$, and $AC = DF$. Prove $\angle A = \angle D$.

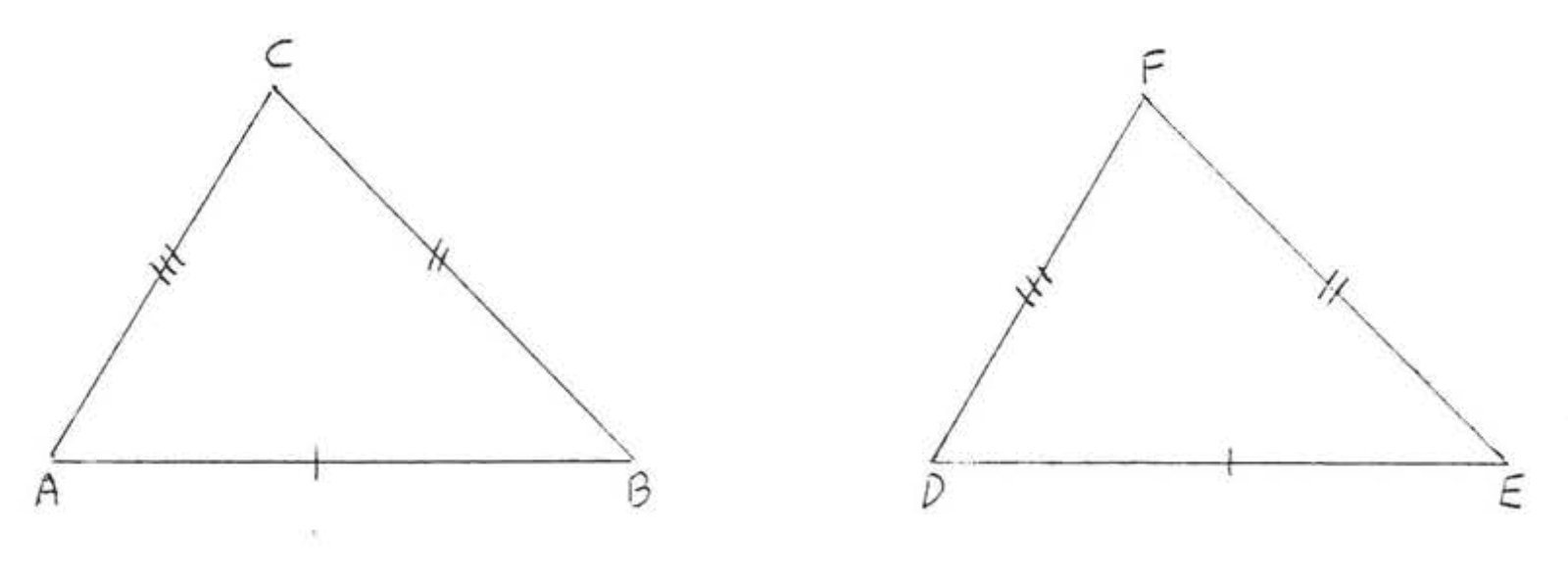
$Screen Shot 2020-11-02 at 5.29.36 PM.png$

10. Given $AC = BC$. $AD = BD$. Prove $\angle ADC = \angle BDC$.

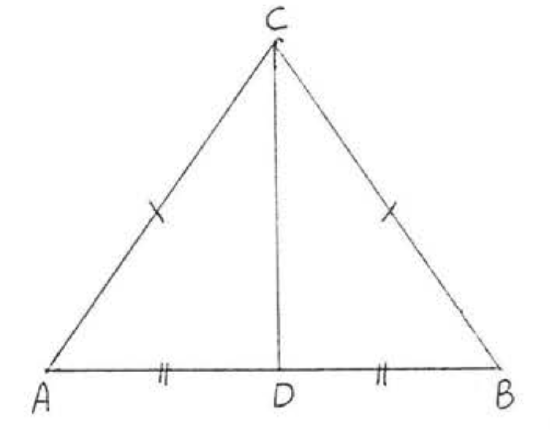
$Screen Shot 2020-11-02 at 5.29.53 PM.png$

11. Given $AB = AD$, $BC = DC$. Prove $\angle BAC = \angle CAD$.

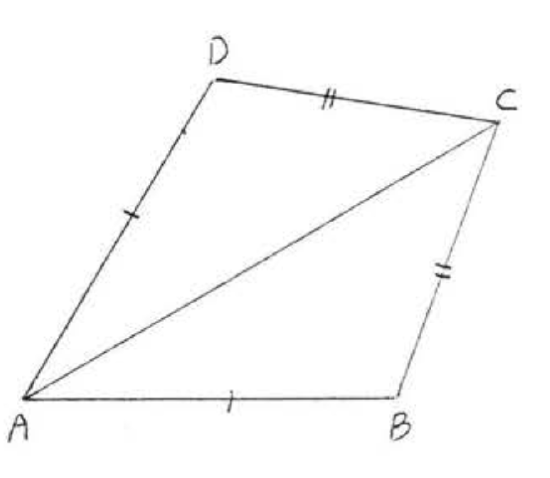
$Screen Shot 2020-11-02 at 5.30.25 PM.png$

12. Given $AB = CD$, $BC = DA$. Prove $\angle BAC = \angle DCA$.

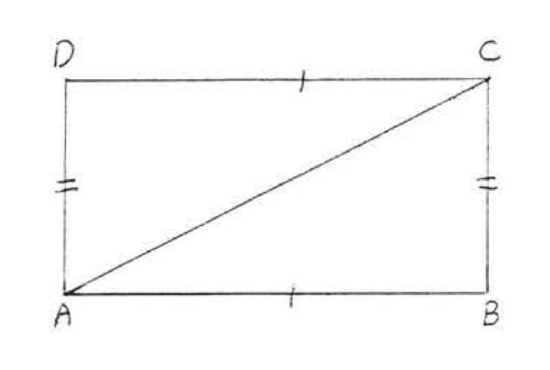
$Screen Shot 2020-11-02 at 5.31.23 PM.png$

13. Given $AE = CE$, $BE = ED$. Prove $AB = CD$.

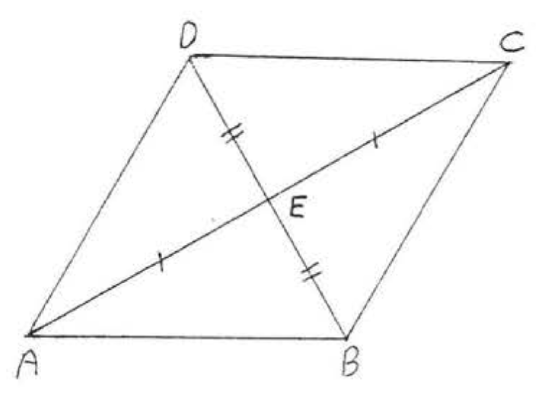
$Screen Shot 2020-11-02 at 5.31.39 PM.png$

14. Given $AB||CD$, $AD||BC$. Prove $AB = CD$.

$Screen Shot 2020-11-02 at 5.31.52 PM.png$

Statement	Reasons
1. \(\angle 1 = \angle 2\).	1. The base angles of isosceles triangle \(CAF\) are equal (Theorem \(\PageIndex{1}\), section 2.5).
2. \(\angle 3 = \angle 4\).	2. The base angles of isosceles triangle \(CBF\) are equal.
3. \(\angle C = \angle F\).	3. \(\angle C = \angle 1 + \angle 3 = \angle 2 + \angle 4 = \angle F\).
4. \(AC = DF\).	4. Given, \(AC = b = e = DF\).
5. \(BC = EF\).	5. Given, \(BC = a = d = EF\).
6. \(\triangle ABC \cong \triangle DEF\).	6. \(SAS = SAS\): \(AC, \angle C, BC\) of \(\triangle ABC = DF\), \(\angle F\), \(EF\) of \(\triangle DEF\).

Search

Text Color

Text Size

Margin Size

Font Type

Statements	Reasons
1. \(AB = DE\).	1. Given.
2. \(BC = EF\).	2. Given.
3. \(AC = DF\).	3. Given.
4. \(\triangle ABC \cong \triangle DEF\).	4. \(SSS = SSS\): \(AB, BC, AC\) of \(\triangle ABC = DE\), \(EF, DF\) of \(\triangle DEF\).
5. \(\angle C = \angle F\).	5. Corresponding angles of congruent triangles are equal.

Theorem \(\PageIndex{1}\): Side-Side-Side (SSS) Theorem

Example \(\PageIndex{1}\)

Proof of Theorem \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Application: Triangular Bracing

Problems