2.5: Isosceles Triangles
- Page ID
- 34128
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
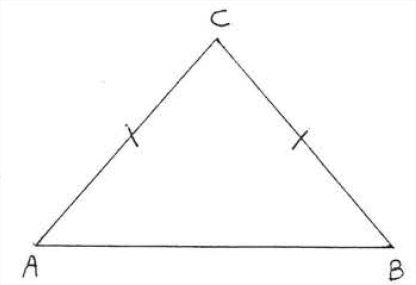
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Section 1.6, we defined a triangle to be isosceles if two of its sides are equal. Figure \(\PageIndex{1}\) shows an isosceles triangle \(\triangle ABC\) with \(AC=BC\). In \(\triangle ABC\) we say that \(\angle A\) is opposite side \(BC\) and \(\angle B\) is opposite side \(AC\).
The most important fact about isosceles triangles is the following:
If two sides of a triangle are equal the angles opposite these sides are equal.
Theorem \(\PageIndex{1}\) means that if \(AC = BC\) in \(\triangle ABC\) then \(\angle A = \angle B\).
Find \(x\):
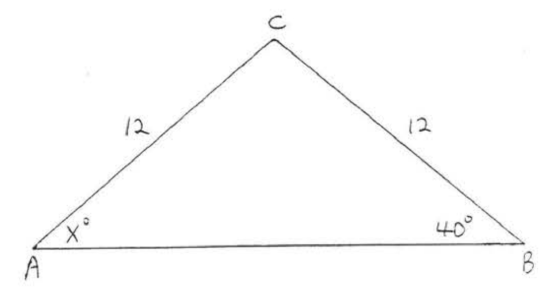
Solution
\(AC = BC\) so \(\angle A = \angle B\). Therefore, \(x = 40\).
Answer: \(x = 40\).
In \(\triangle ABC\) if \(AC = BC\) then side \(AB\) is called the base of the triangle and \(\angle A\) and \(\angle B\) are called the base angles. Therefore Theorem \(\PageIndex{1}\) is sometimes stated in the following way: "The base angles of an isosceles triangle are equal,"
Proof of Theorem \(\PageIndex{1}\): Draw \(CD\), the angle bisector of \(\angle ACB\) (Figure \(\PageIndex{2}\)). The rest of the proof will be presented in double-column form. We have given that \(AC = BC\) and \(\angle ACD = \angle BCD\). We must prove \(\angle A = \angle B\).
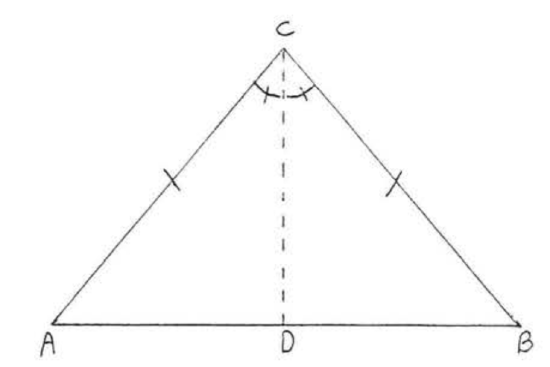
| Statements | Reasons |
|---|---|
| 1. \(AC = BC\). | 1. Given, \(\triangle ABC\) is isosceles. |
| 2. \(\angle ACD = \angle BCD\). | 2. Given, \(CD\) is the angle bisector of \(\angle ACB\). |
| 3. \(CD = CD\). | 3. Identity. |
| 4. \(\triangle ACD \cong \triangle BCD\). | 4. \(SAS = SAS\): \(AC, \angle C, CD\) of \(\triangle ACD = BC\), \(\angle C, CD\) of \(\triangle BCD\). |
| 5. \(\angle A = \angle B\). | 5. Corresponding angles of congruent trianglesare equal. |
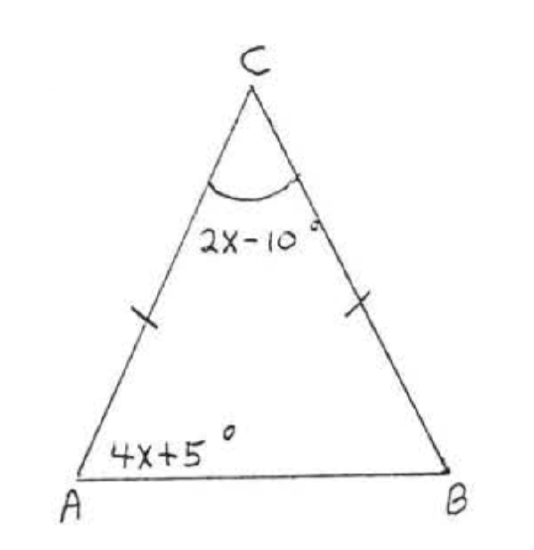
Find \(x, \angle A, \angle B\) and \(\angle C\):
Solution
\(\angle B = \angle A = 4x + 5^{\circ}\) by Theorem \(\PageIndex{1}\). We have
\[\begin{array} {rcl} {\angle A + \angle B + \angle C} & = & {180^{\circ}} \\ {4x + 5 + 4x + 5 + 2x - 10} & = & {180} \\ {10x} & = & {180} \\ {x} & = & {18} \end{array}\]
\(\angle A = \angle B = 4x + 5^{\circ} = 4(18) + 5^{\circ} = 72 + 5^{\circ} = 77^{\circ}\).
\(\angle C = 2x - 10^{\circ} = 2(18) - 10^{\circ} = 36 - 10^{\circ} = 26^{\circ}\).
Check
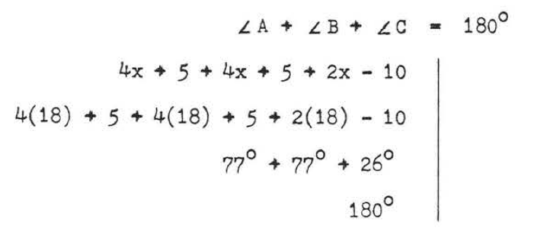
Answer
\(x = 18\), \(\angle A = 77^{\circ}\), \(\angle B = 77^{\circ}\), \(\angle C = 26^{\circ}\).
In Theorem \(\PageIndex{1}\) we assumed \(AC = BC\) and proved \(\angle A = \angle B\). We will now assume \(\angle A = \angle B\) and prove \(AC = BC\). '1ihen the assumption and conclusion of a statement are interchanged the result is called the converse of the original statement.
If two angles of a triangle are equal the sides opposite these angles are equal.
If Figure 4, if \(\angle A = \angle B\) then \(AC = BC\).
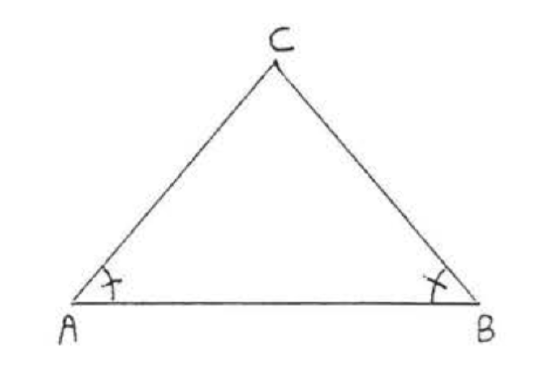
Find \(x\)
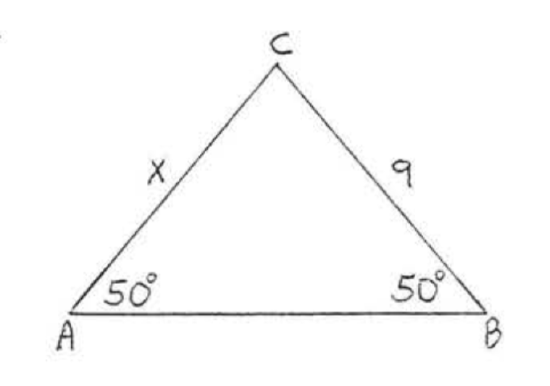
Solution
\(\angle A = \angle B\) so \(x = AC = BC = 9\) by Theorem \(\PageIndex{2}\).
Answer
\(x = 9\).
Proof of Theorem \(\PageIndex{2}\): Draw \(CD\) the angle bisector of \(\angle ACB\) (Figure \(\PageIndex{5}\)). We have \(\angle ACD = \angle BCD\) and \(\angle A = \angle B\). We must prove \(AC = BC\).
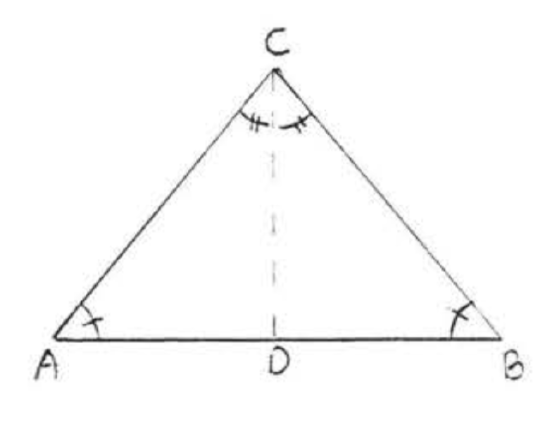
| Statements | Reasons |
|---|---|
| 1. \(\angle A = \angle B\). | 1. Given. |
| 2. \(\angle ACD = \angle BCD\). | 2. Given. |
| 3. \(CD = CD\). | 3. Identity. |
| 4. \(\triangle ACD \cong \triangle BCD\). | 4. \(AAS = AAS\): \(\angle A, \angle C, CD\) of \(\triangle ACD = \angle B\), \(\angle C\), \(CD\) of \(triangle BCD\). |
| 5. \(AC = BC\). | 5. Corresponding sides of congruent triangles are equal |
The following two theorems are corollaries (immediate consequences) of the two preceding theorems:
An equilateral triangle is equiangular.
In Figure \(\PageIndex{7}\), if \(AB = AC = BC\) then \(\angle A = \angle B = \angle C\).
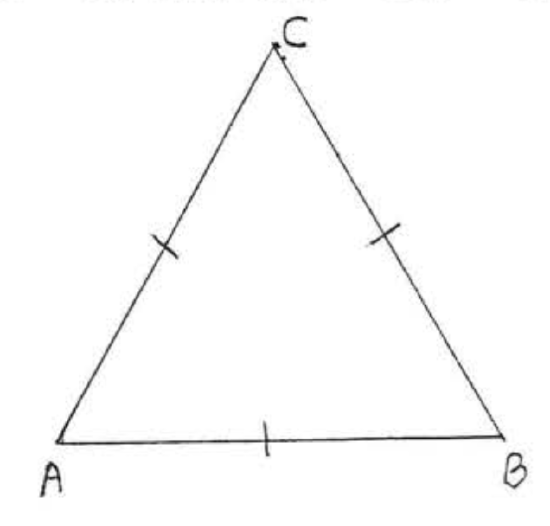
- Proof
-
\(AC = BC\) so by Theorem \(\PageIndex{1}\) \(\angle B = \angle C\). Therefore \(\angle A = \angle B = \angle C\).
Since the sum of the angle is \(180^{\circ}\) we must have in fact that \(\angle A = \angle B = \angle C = 60^{\circ}\).
An equiangular triangle is equilateral.
In Figure \(\PageIndex{8}\), if \(\angle A = \angle B = \angle C\) then \(AB = AC = BC\).
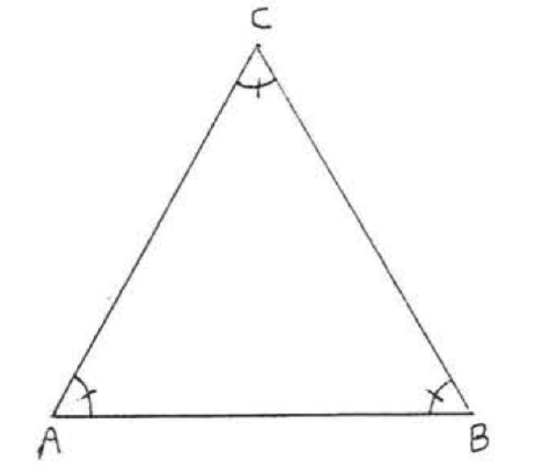
- Proof
-
\(\angle A = \angle B\) so by Theorem \(\PageIndex{2}\), \(AC = BC\), \(\angle B = \angle C\) by Theorem \(\PageIndex{2}\), \(AB = AC\). Therefore \(AB = AC = BC\).
Find \(x\), \(y\) and \(AC\):
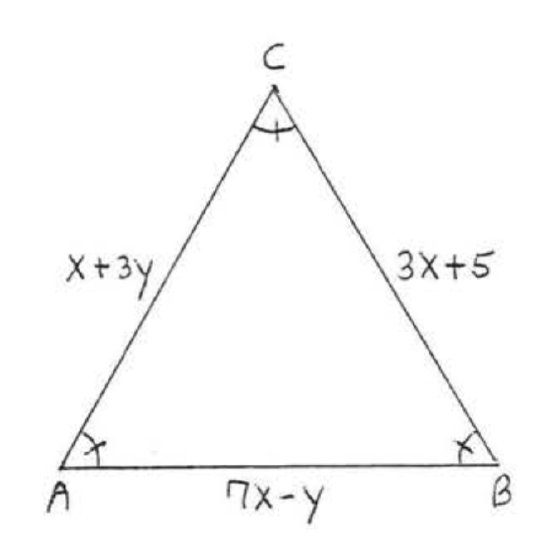
Solution
\(\triangle ABC\) is equiangular and so by Theorem \(\PageIndex{4}\) is equilateral.
Therefore \(\begin{array} {rcl} {AC} & = & {AB} \\ {x + 3y} & = & {7x - y} \\ {x - 7x + 3y + y} & = & {0} \\ {-6x + 4y} & = & {0} \end{array}\) and \(\begin{array} {rcl} {AB} & = & {BC} \\ {7x - y} & = & {3x + 5} \\ {7x - 3xy - y} & = & {5} \\ {4x - y} & = & {5} \end{array}\)
We have a system of two equations in two unknowns to solve:
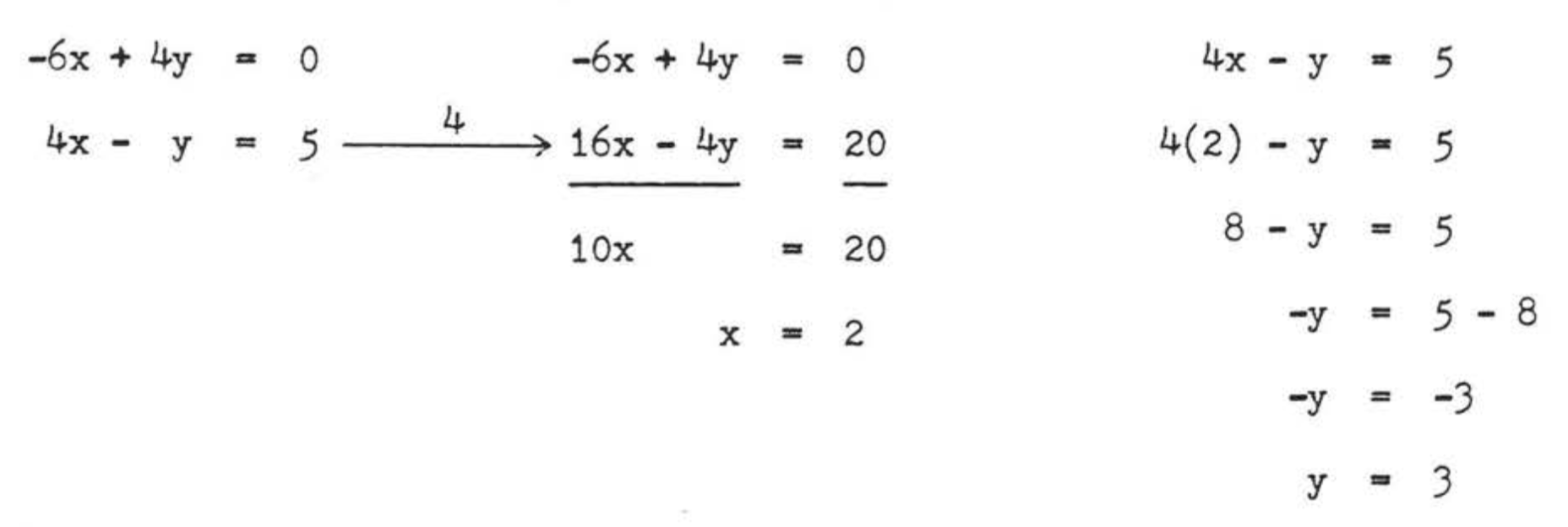
Check:

Answer: \(x = 2\), \(y = 3\), \(AC = 11\).
Theorem \(\PageIndex{1}\), the isosceles triangle theorem, is believed to have first been proven by Thales (c. 600 B,C,) - it is Proposition 5 in Euclid's Elements. Euclid's proof is more complicated than ours because he did not want to assume the existence of an angle bisector, Euclid's proof goes as follows:
Given \(\triangle ABC\) with \(AC = BC\) (as in Figure \(\PageIndex{1}\) at the beginning of this section), extend \(CA\) to \(D\) and \(CB\) to \(E\) so that \(AD = BE\) (Figure \(\PageIndex{9}\)). Then \(\triangle DCB \cong \triangle ECA\) by \(SAS = SAS\). The corresponding sides and angles of the congruent triangles are equal, so \(DB = EA\), \(\angle 3 = \angle 4\) and \(\angle 1 + \angle 5 = \angle 2 + \angle 6\). Now \(\triangle ADB \cong \triangle BEA\) by \(SAS = SAS\). This gives \(\angle 5 = \angle 6\) and finally \(\angle 1 = \angle 2\).
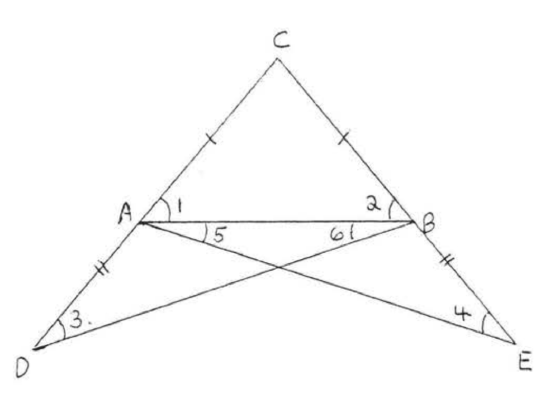
This complicated proof discouraged many students from further study in geometry during the long period when the Elements was the standard text, Figure \(\PageIndex{9}\) resembles a bridge which in the Middle Ages became known as the "bridge of fools," This was supposedly because a fool could not hope to cross this bridge and would abandon geometry at this point.
Problems
For each of the following state the theorem(s) used in obtaining your answer.
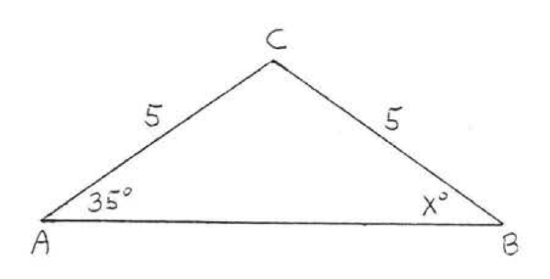
1. Find \(x\):
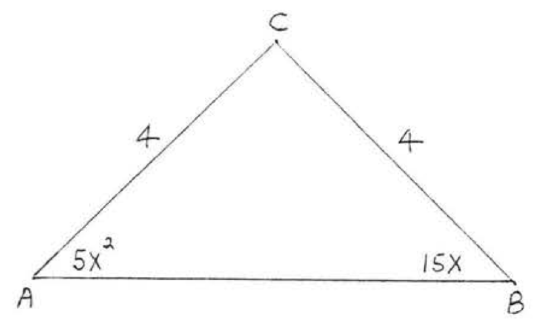
2. Find \(x\), \(\angle A\), and \(\angle B\):
3. Find \(x\):
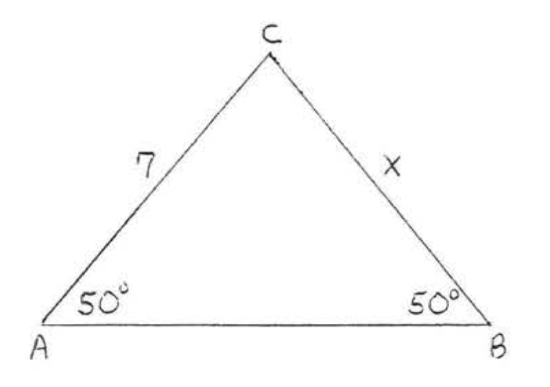
4. Find \(x\), \(AC\), and \(BC\):
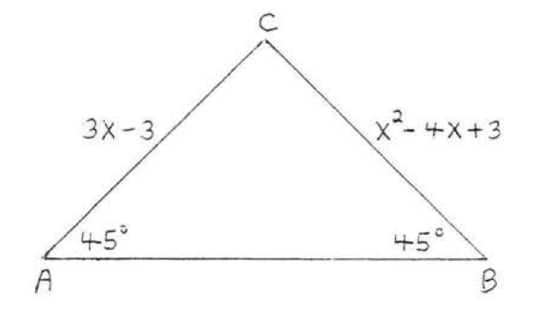
5. Find \(x\):
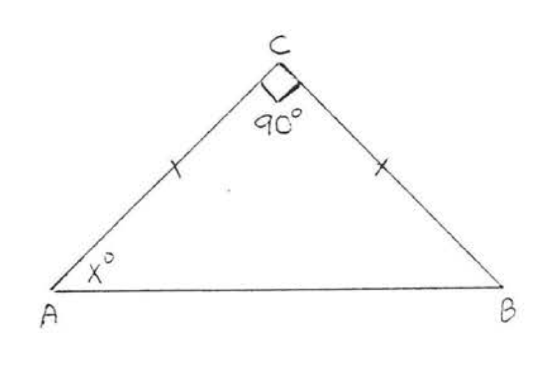
6. Find \(x\):
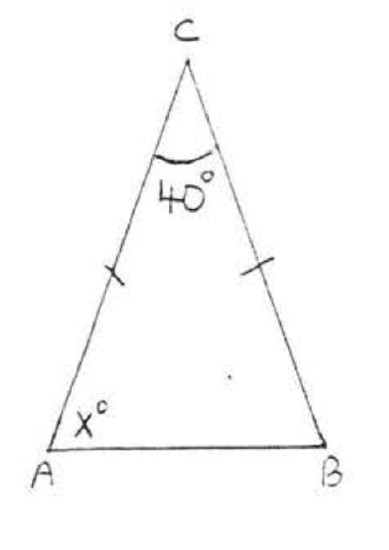
7. Find \(x, \angle A, \angle B\), and \(\angle C\):
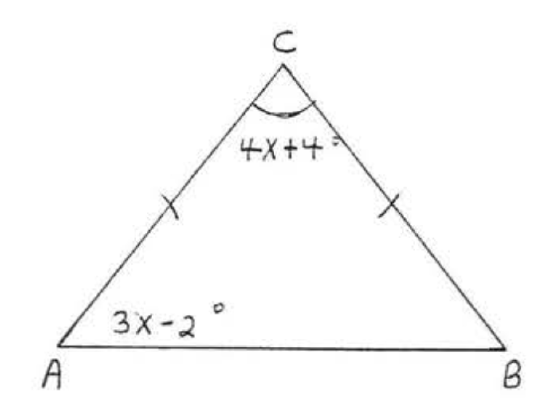
8. Find \(x, \angle A, \angle B\), and \(\angle C\):
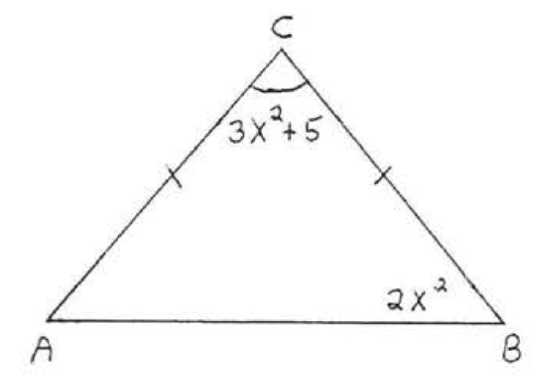
9. Find \(x, AB, AC\), and \(BC\):
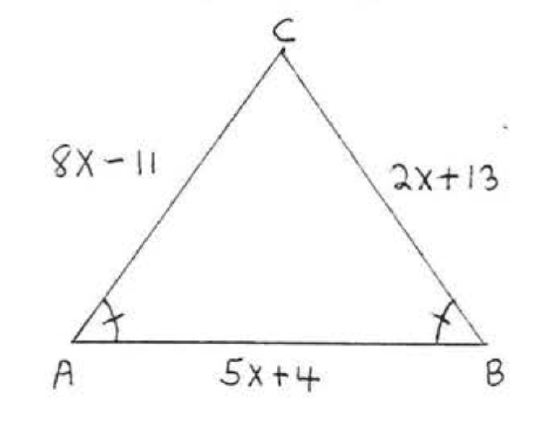
10. Find \(x, AB, AC\), and \(BC\):
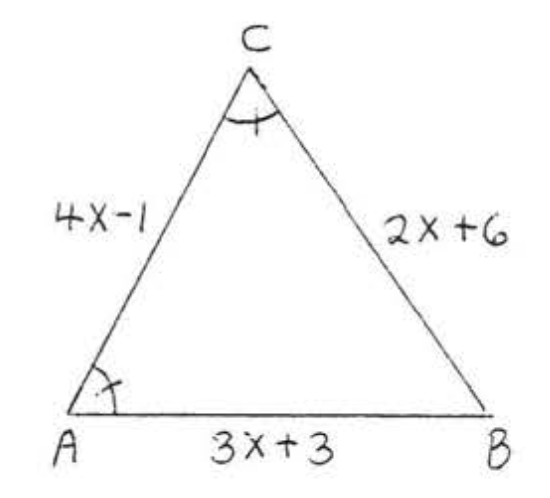
11. Find \(x, y\), and \(AC\):
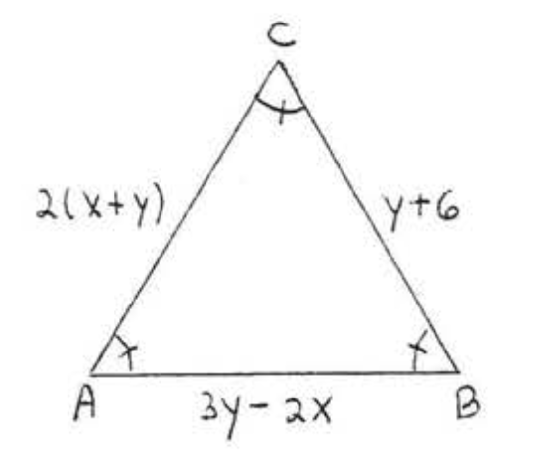
12. Find \(x, y\), and \(AC\):
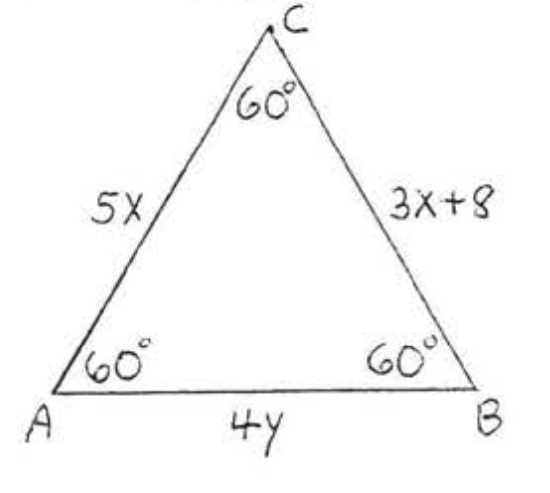
13. Find \(x\):
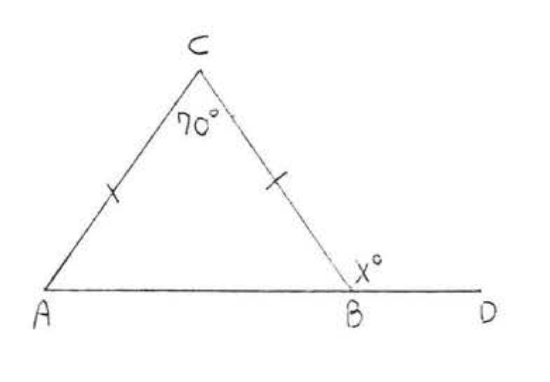
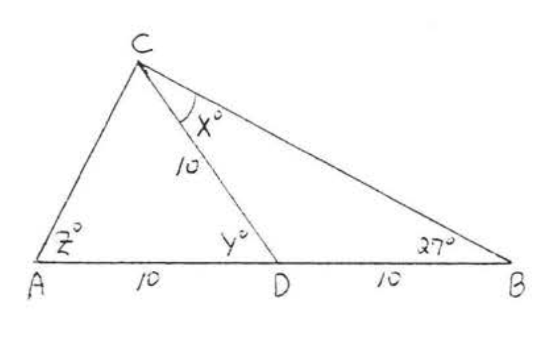
14. Find \(x, y\), and \(z\):