2.4: Proving Lines and Angles Equal

Last updated
Save as PDF

Page ID: 34127

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

We can prove lines and angles equal if we can show they are corresponding parts of congruent triangles, We find it convenient to present these proofs in double-column form with statements in the left columnand the reason for each statement in the right.

Example $\PageIndex{1}$

Given $AB || CD$ and $AB = CD$ prove $AD = BC$

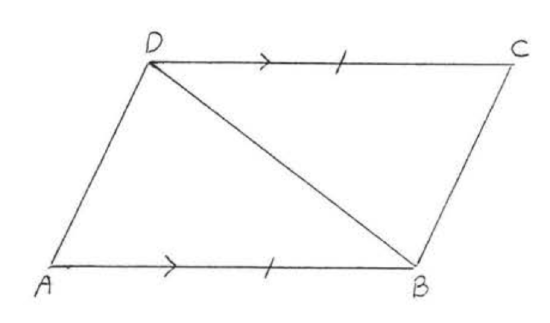
$屏幕快照 2020-10-30 下午5.50.12.png$

Solution

Statements	Reasons
1. $AB = CD$.	1. Given.
2. $\angle ABD = \angle CDB$.	2. Alternate interior angles of parallel lines $(AB \|\| CD)$ are equal.
3. $BD = DB$.	3. Identity.
4. $\triangle ABD \cong \triangle CDB$	4. $SAS = SAS$: $AB, \angle B, BD$ of $\triangle ABD = CD$, $\angle D$, $DB$ of $\triangle CDB$.
5. $AD = BC$	5. Corresponding sides of congruent triangles are equal,

Explanation: Each of the first three statements says that a side or angle of $\triangle ABD$ is equal to the corresponding side or angle of $\triangle CDB$, To arrive at these statements, we should first write the congruence statement using the methods of the previous sections. We then select three pairs of corresponding sides or angles which are equal because of one of the following reasons:

Reasons Lines Are Equal

Given. This means we are asked to assume the lines are equal at the beginning of the exercise, For example, the problem will state "given $AB = CD$" or $AB$ and $CD$ will be marked the same way in the diagram.
Identity. This means the identical line segment appears in both triangles, For example, $BD$ and $DB$ represent the same line segment, Of course the length of a line segment is equal to itself.

Reasons Angles Are Equal

Given.
Identity.
Alternate interior angles of parallel lines are equal. To apply this reason we must be given that the lines are parallel.
Corresponding angles of parallel lines equal.
Vertical angles are equal.

These are not the only possible reasons but they are all that we will use at first.

We should also select the three pairs of equal sides or angles so that one of the reasons $SAS = SAS$, $ASA = ASA$, or $AAS = AAS$ can be used to justify the congruence statement in statement 4, In sections 2.6 and 2.7, we will give some additional reasons for two triangles to be congruent.

Statement 5 is the one we wish to prove, The reason is that corresponding sides (or angles) of congruent triangles are equal. Wecan use this reason here because the triangles have already been proven congruent in statement 4,

One final comment, Notice how the solution of Example $\PageIndex{1}$ conforms with our original definition of proof, Each new statement is shown to be true by using previous statements and reasons which have already been established.

Let us give another example:

Example $\PageIndex{2}$

Given $QP || ST$ and $QR = TR$ prove $PR = SR$.

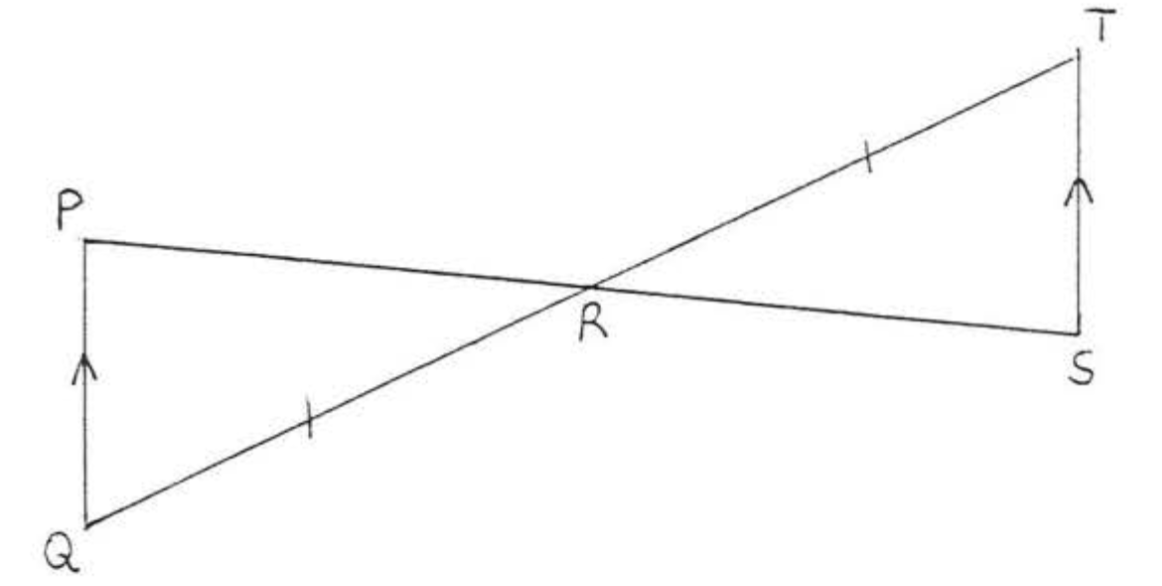
$屏幕快照 2020-10-30 下午6.02.31.png$

Solution

Statements	Reasons
1. $QR = TR$	1. Given.
2. $\angle Q = \angle T.$	2. Alternate interior angles of parallel lines ($QP \|\| ST$) are equal.
3. $\angle PRQ = \angle SRT$.	3. Vertical angles are equal.
4. $\triangle PQR \cong \triangle STR$.	4. $ASA = ASA: \angle Q, QR, \angle R$ of $\triangle PQR = \angle T$, $TR, \angle R$ of $\triangle STR$.
5. $PR = SR$.	5. Corresponding sides of congruent triangles are equal,

Problems

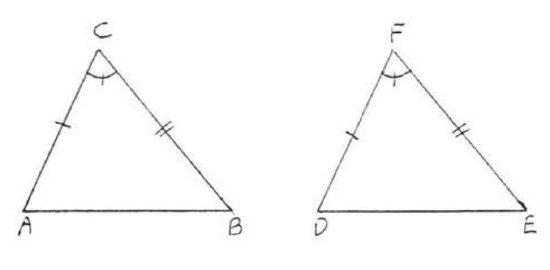
1. Given $\angle A = \angle D$, $\angle B = \angle E$, $AB = DE$. Prove $AC = DF$.

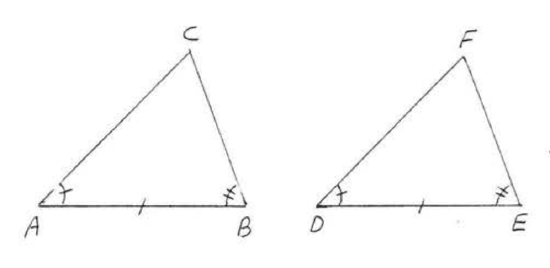
$Screen Shot 2020-10-30 at 6.14.23 PM.png$

2. Given $AC= DF$, $BC = EF$, $\angle C = \angle F$. Prove $AB = DE$.

$Screen Shot 2020-10-30 at 6.14.42 PM.png$

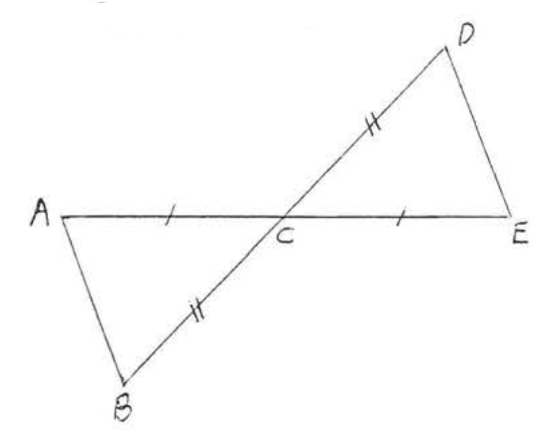
3. Given $AC = EC$ and $BC = DC$. Prove $AB = ED$.

$Screen Shot 2020-10-30 at 6.15.21 PM.png$

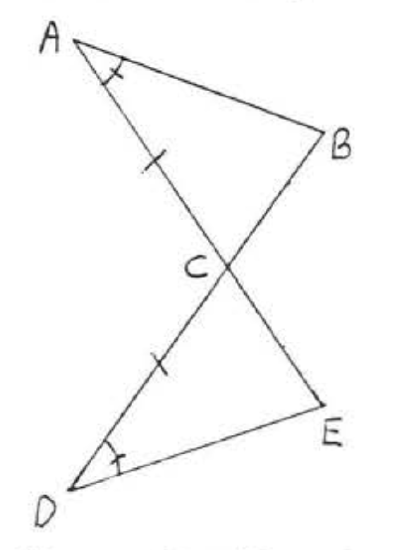
4. Given $AC = DC$, $\angle A = \angle D$. Prove $BC = EC$.

$Screen Shot 2020-10-30 at 6.15.36 PM.png$

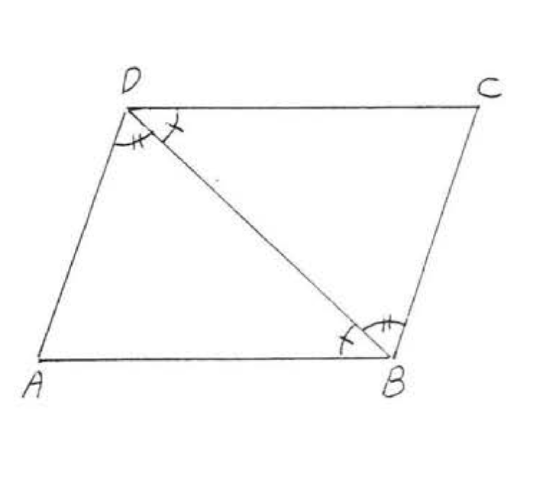
5. Given $\angle ABD = \angle CDB$ and $\angle ADB = \angle CBD$. Prove $AB = CD$.

$Screen Shot 2020-10-30 at 6.15.48 PM.png$

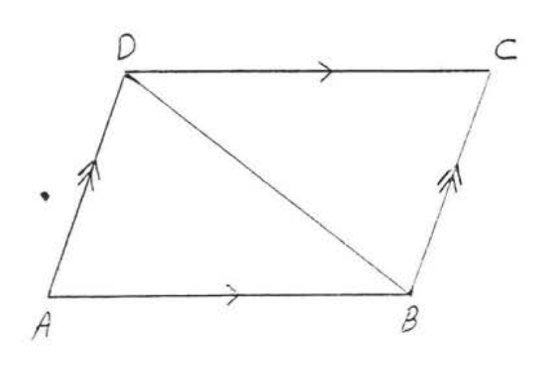
6. Given $AB || CD$ and $AD || CB$. Prove $AB = CD$.

$Screen Shot 2020-10-30 at 6.15.59 PM.png$

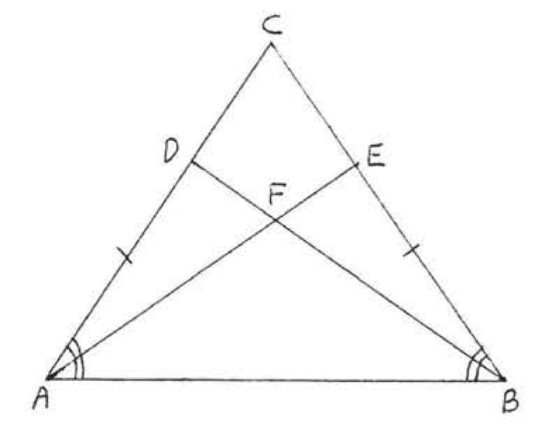
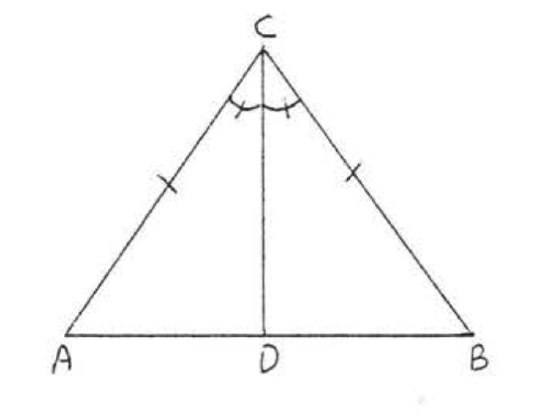
7. Given $AC = BC$ and $\angle ACD = \angle BCD$. Prove $\angle A = \angle B$.

$Screen Shot 2020-10-30 at 6.16.32 PM.png$

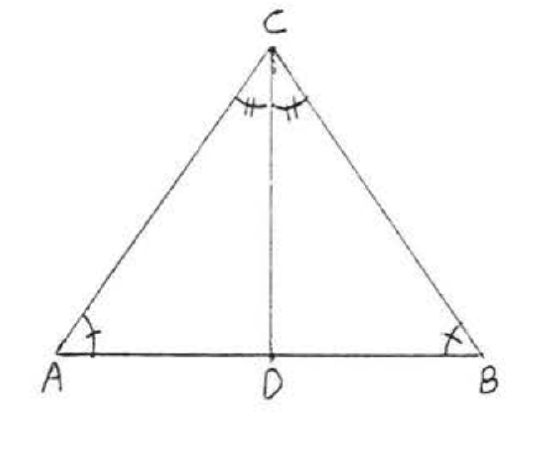
8. Given $\angle A = \angle B$, $\angle ACD = \angle BCD$. Prove $AC = BC$.

$Screen Shot 2020-10-30 at 6.16.45 PM.png$

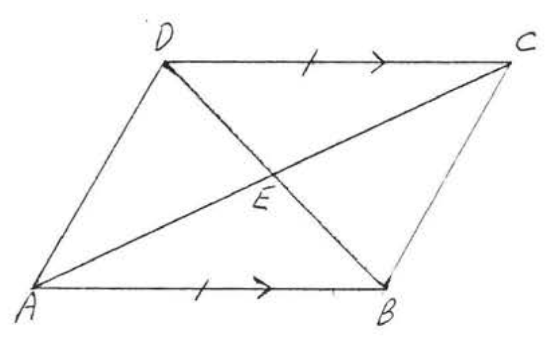
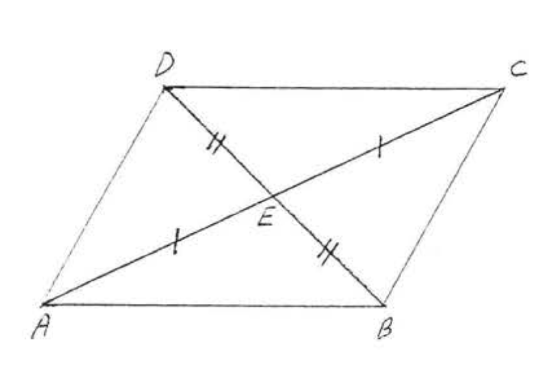
9. Given $AB || CD$ and $AB = CD$. Prove $AE = CE$. (Hint: Show $\triangle ABE \cong \triangle CDE$)

$Screen Shot 2020-10-30 at 6.16.58 PM.png$

10. Given $AE = CE$ and $BE = DE$. Prove $\angle BAC = \angle CDB$.

$Screen Shot 2020-10-30 at 6.17.17 PM.png$

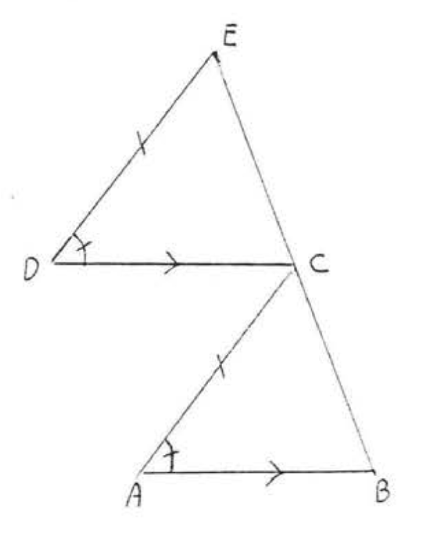
11. Given $\angle A = \angle D$, $AC = DE$, $AB || DC$. Prove $BC = CE$.

$Screen Shot 2020-10-30 at 6.17.30 PM.png$

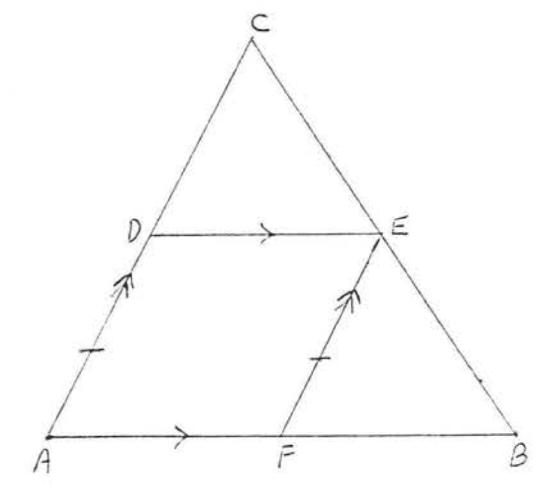
12. Given $AB || DE$, $AC || FE$ and $DC = FE$. Prove $BE = EC$.

$Screen Shot 2020-10-30 at 6.17.55 PM.png$

13. Given $AD = BC$ and $\angle BAD = \angle ABC$. Prove $AC = BD$. (Hint: Show $\triangle ABD \cong \triangle BAC$)

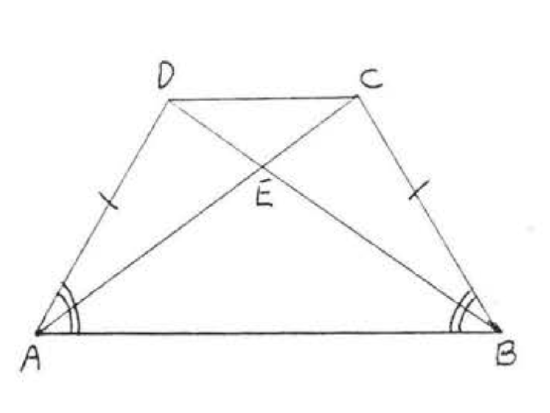
$Screen Shot 2020-10-30 at 6.18.11 PM.png$

14. Given $AD = BE$, $\angle BAC = \angle ABC$. Prove $AE = BD$.

$Screen Shot 2020-10-30 at 6.18.26 PM.png$

Statements	Reasons
1. \(AB = CD\).	1. Given.
2. \(\angle ABD = \angle CDB\).	2. Alternate interior angles of parallel lines \((AB \|\| CD)\) are equal.
3. \(BD = DB\).	3. Identity.
4. \(\triangle ABD \cong \triangle CDB\)	4. \(SAS = SAS\): \(AB, \angle B, BD\) of \(\triangle ABD = CD\), \(\angle D\), \(DB\) of \(\triangle CDB\).
5. \(AD = BC\)	5. Corresponding sides of congruent triangles are equal,

Statements	Reasons
1. \(QR = TR\)	1. Given.
2. \(\angle Q = \angle T.\)	2. Alternate interior angles of parallel lines (\(QP \|\| ST\)) are equal.
3. \(\angle PRQ = \angle SRT\).	3. Vertical angles are equal.
4. \(\triangle PQR \cong \triangle STR\).	4. \(ASA = ASA: \angle Q, QR, \angle R\) of \(\triangle PQR = \angle T\), \(TR, \angle R\) of \(\triangle STR\).
5. \(PR = SR\).	5. Corresponding sides of congruent triangles are equal,

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Problems