1.1: Introduction to Euclid’s Elements

Last updated
Save as PDF

Page ID: 107092

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

As an introduction, we’ll cover only Propositions 1-28 of Book 1. This is an introduction to neutral or absolute geometry that subsumes both Euclidean and hyperbolic geometry. The given website is the Sir Thomas L. Heath translation and his very informative commentary; i.e., the (cheap!) Dover books in electronic form. Clicking on the proposition number brings up the statement and its historical proof. As an example, here is Proposition 5 the famous Pons Asinorum (Asses’ Bridge), a double entendre from its shape and "honoring" those burros who cannot cross it (you get the idea). All the way back to the Greeks, proofbased geometry separated cognoscenti from commoner. Although used here, we will try to avoid identifying same-sized line segments or angles as "equal" because they are also sets of points and two sets are defined to be equal if they contain exactly the same elements. Congruent is the word we will ordinarily use or the term equal in measure, that theoretical "measure" of perfection that can never be achieved by measuring, but many great geometers have used the term "equal" in this context. Please do not.

Proposition 5

In isosceles triangles, the angles at the base are equal to one another, and, if the equal straight lines be produced further, the angles under the base will be equal to one another.

Proof: Let $\Delta ABC$ be an isosceles triangle having the side $\overline{AB}$ equal to the side $\overline{AC}$; and let the straight lines $\overleftrightarrow{BD},$ $\overleftrightarrow{CE}$ be produced further in a straight line with $\overline{AB}$, $\overline{AC}$. [Post. 2]

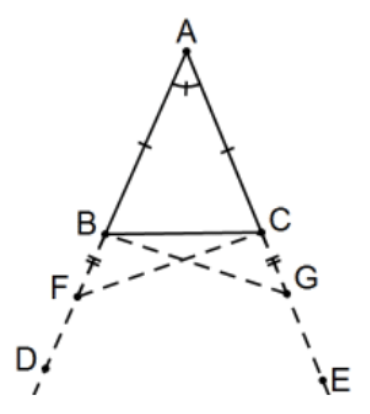
$Screen Shot 2022-06-23 at 10.52.40 AM.png$

I say that the angle $\angle ABC$ is equal to the angle $\angle ACB$, and the angle $\angle CBD$ to the angle $\angle BCE.$

Let a point $F$ be taken at random on $\mathrm{BD}$; from $\mathrm{AE}$ the greater $[\mathrm{AE}>\mathrm{AD}$ ] let AG be cut off equal to AF the less; and let the straight lines FC, GB be joined. [Post. 1]

Then, since $\mathrm{AF}$ is equal to $\mathrm{AG}$ and $\mathrm{AB}$ to $\mathrm{AC}$, the two sides $\mathrm{FA}, \mathrm{AC}$ are equal to the two sides $\mathrm{GA}$, $\mathrm{AB}$, respectively; and they contain a common angle, the angle FAG.

Therefore the base FC is equal to the base GB, and the triangle AFC is equal to the triangle AGB, and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend, that is, the angle ACF to the angle ABG, and the angle AFC to the angle AGB.

And, since the whole $\mathrm{AF}$ is equal to the whole $\mathrm{AG}$, and in these $\mathrm{AB}$ is equal to $\mathrm{AC}$, the remainder $\mathrm{BF}$ is equal to the remainder CG.

But FC was also proved equal to GB; therefore the two sides $\mathrm{BF}, \mathrm{FC}$ are equal to the two sides CG, GB respectively; and the angle BFC is equal to the angle CGB, while the base $\mathrm{BC}$ is common to them; therefore the triangle BFC is also equal to the triangle CGB, and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend; therefore the angle FBC is equal to the angle GCB, and the angle BCF to the angle CBG.

Accordingly, since the whole angle ABG was proved equal to the angle ACF, and in these the angle CBG is equal to the angle BCF, the remaining angle $\mathrm{ABC}$ is equal to the remaining angle ACB; and they are at the base of the triangle ABC. But the angle FBC was also proved equal to the angle GCB; and they are under the base.

QED.

[Quod Erat Demonstrandum, Latin for "that which was to be demonstrated.”]

Note

QEF is another but less common, "Quod Erat Faciendum, "that which was to have been done". Are there easier proofs? Of course, we saw several in the Introduction! But we can’t just start in anywhere. Why, for example, start with Prop 5? In part, because the beginning of the Elements is a little shaky and we’ll only partly "fix it up". If we spent too much time on a modern approach, we wouldn’t get beyond that.

Contributors

http://aleph0.clarku.edu/ djoyce/java/elements/bookI/bookI.html - Used with owner’s permission. [Or just Google "Euclid Book 1" if this URL (and very useful site) becomes unavailable. For example: http://www.perseus.tufts.edu/hopper/text?doc=Euc.+1]