1.2: Triangles

Suggested Prerequisite Topics

This section is designed assuming you understand the following topics from Arithmetic and Algebra.

• Using technology to approximate irrational numbers (specifically, radicals)
• Inequality notation
• Solving linear inequalities in one variable
• Simplifying radicals (specifically, quantities)
• Solving equations via Extraction of Roots

Learning Objectives

• Find the missing angle within a triangle using the Triangle Sum.
• Use the Triangle Inequality to determine constraints on an unknown side length of a triangle.
• Use the Pythagorean Theorem to find the third side of a right triangle.
• Find the missing sides of a \( 30^{ \circ } \)-\( 60^{ \circ } \)-\( 90^{ \circ } \) or \( 45^{ \circ } \)-\( 45^{ \circ } \)-\( 90^{ \circ } \) triangle given one side.
• Solve real-world applications requiring the Pythagorean Theorem or the special triangles.

Triangle Basics

The study of Trigonometry inevitably involves understanding everything we possibly can about triangles. Starting simple, when three line segments bound a portion of the plane, the resulting shape is called a three-sided polygon, better known as a triangle. The line segments are called the sides of the triangle. In Figure \( \PageIndex{ 1 } \), the sides are denoted \( \overline{AB} \), \( \overline{BC} \), and \( \overline{AC} \). A point where two sides meet is called a vertex of the triangle. Again, in Figure \( \PageIndex{ 1 } \), the vertices (plural of vertex) are \( A \), \( B \), and \( C \). The angle formed in the triangle's interior where two sides meet is called an angle of the triangle. The angles in Figure \( \PageIndex{ 1 } \) are denoted \( \angle A \), \( \angle B \), and \( \angle C \). Using the notation \( \triangle A B C \), we refer to the triangle by its vertices.

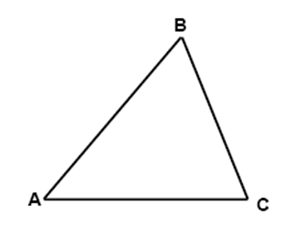
Figure \( \PageIndex{ 1 } \): \( \triangle A B C \)

If one tears off the corners of any triangle and lines them up, as shown in Figure \( \PageIndex{ 2 } \), they will always form a straight angle.

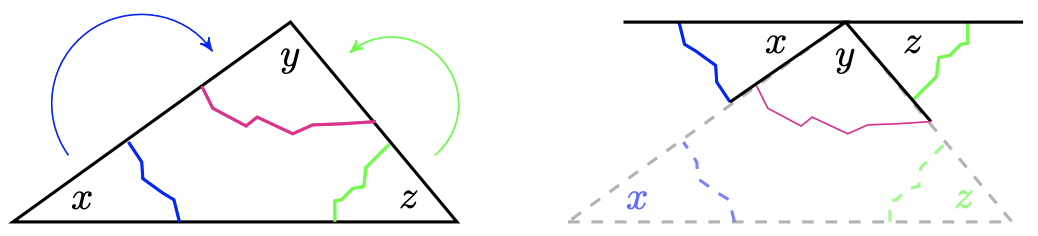
Figure \( \PageIndex{ 2 } \): Tearing corners from a triangle to form a straight angle

Theorem: Triangle Sum

The sum of the interior angles in a triangle is \( 180^{\circ} \).

Proof

Given the triangle, \( \triangle ABC \), draw a line parallel to side \( BC \) going through vertex \( A \) (see the figure below).

Figure \( \PageIndex{ 3 } \)

Since \( \angle q + \angle a + \angle p \) forms a straight angle,\[ \angle q + \angle a + \angle p = 180^{\circ}. \label{sumang} \]Moreover, the line segment \( AC \) is a transversal for the parallel lines \( BC \) and \( DE \). Therefore, \( \angle c = \angle p \). By a similar argument, \( \angle b = \angle q \). Substituting these into Equation \( \ref{sumang} \), we arrive at\[ \angle b + \angle a + \angle c = 180^{\circ}. \nonumber \]Thus, the sum of the angles of a triangle is \( 180^{\circ} \).

Example \(\PageIndex{1}\)

Two of the angles in the triangle shown below are \(25^{\circ}\) and \(115^{\circ}\). Find the third angle.

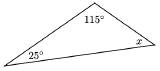
Solution

To find the third angle, we write an equation.\[\begin{array}{crrclr}
& & x+25+115 & = & 180 & (\text{Triangle Sum}) \\
\scriptscriptstyle\mathrm{Arithmetic} & \implies & x+140 & = & 180 & (\text{add}) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \textrm{Algebra} & \implies & x & = & 40 & (\text{subtract }140\text{ from both sides})\\
\end{array} \nonumber \]The third angle is \(40^{\circ}\).

What does the \( \mathrm{Arithmetic} \) and \( \xcancel{\textrm{Arithmetic}} \) mean?

To get you used to the Mathematical Mantra, every once in a while I will include the "thought processes" during solutions. Just to review, we perform Mathematics in the order we learned it - Arithmetic, Algebra, Trigonometry, \( \ldots \). At each step during a "mechanical" solution process, we should pause and ask ourselves if there is some simple Arithmetic to be done. If not, we move on to any Algebra that can be done. If there is no Algebra to be done, we then move on to Trigonometry.

Thus,

• "\( \mathrm{Arithmetic} \implies\)" in a solution means that there is some Arithmetic we could do to clean up the previous expression
• "\( \xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} \implies\)" means there isn't any Arithmetic but there is some Algebra we could use to clean up the previous expression or equation
• "\( \xcancel{\mathrm{Arithmetic}} \to \xcancel{\mathrm{Algebra}} \to \mathrm{Trigonometry} \implies\)" means there isn't any Arithmetic nor is there any Algebra that can be done to clean up the previous step, so we need to start looking at doing something from Trigonometry.

Checkpoint \(\PageIndex{1}\)

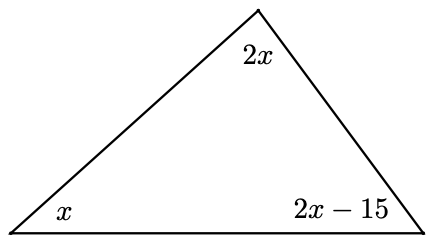
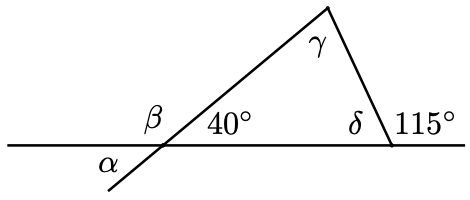
Find all the unknown angles in each figure.

1. 
   
2. 
   

Answer

1. \(x = 39^{\circ}, 2x = 78^{\circ}, 2x-15 = 63^{\circ}\)
2. \(\alpha=40^{\circ}, \beta=140^{\circ}, \gamma=75^{\circ}, \delta=65^{\circ}\)

In any triangle, the longest side is always opposite the largest angle, and the shortest side is opposite the smallest, as illustrated in Figure \( \PageIndex{ 3 } \). Although obvious to most people, this fact will become invaluable as we move through Trigonometry.

Figure \( \PageIndex{ 3 } \)

Notation: Angles and Sides of a Triangle

It is common (though not necessary) to label the angles of a triangle with capital letters and the side opposite each angle with the corresponding lowercase letter, as shown in the figure below. We will follow this practice unless indicated otherwise.

Example \( \PageIndex{ 2 } \)

In \(\triangle F G H, \angle F=48^{\circ}\), and \(\angle G\) is obtuse. Side \(f\) is 6 feet long. What can be concluded about the other sides?

Solution

Because \(\angle G\) is greater than \(90^{\circ}\), we know that \(\angle F+\angle G\) is greater than \(90^{\circ}+48^{\circ}=138^{\circ}\), so \(\angle H\) is less than \(180^{\circ}-138^{\circ}=42^{\circ}\). Thus, \(\angle H<\angle F<\angle G\), and consequently \(h<f<g\). We can conclude that \(h<6\) feet long, and \(g>6\) feet long.

Checkpoint \( \PageIndex{ 2 } \)

In triangle \(\triangle R S T\), \(\angle S\) is \(72^{\circ}\). The remaining two angles have the same size. Which side is longer, \(s\) or \(t\)?

Answer

\(s\) is longer

The Triangle Inequality

The sum of the lengths of any two sides of a triangle must be greater than the third side; otherwise, the two sides will not meet to form a triangle. This fact is known as the triangle inequality. The theorem is presented without proof (however, you can always find a suitable proof online).

Theorem: Triangle Inequality

In any triangle, we must have that\[p + q > r, \nonumber \]where \(p, q\), and \(r\) are the lengths of the sides of the triangle (see the figure below).

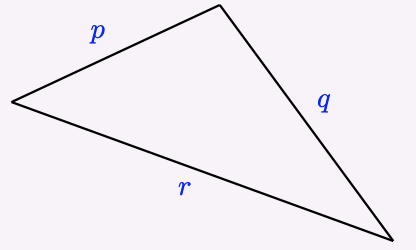
We cannot use the triangle inequality to find the exact lengths of a triangle's sides, but we can find the largest and smallest possible values for the length.

Example \( \PageIndex{ 3 } \)

Two sides of a triangle have lengths 7 inches and 10 inches, as shown below. What can be said about the length of the third side?

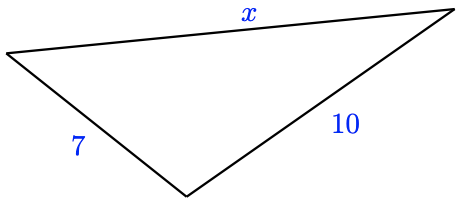
Solution

We let \(x\) represent the length of the third side of the triangle. By looking at each side in turn, we can apply the triangle inequality in three different ways to get\[7<x+10, \quad 10<x+7, \quad \text { and } \quad x<10+7 \nonumber\]We solve each of these inequalities to find\[-3<x, \quad 3<x, \quad \text { and } \quad x<17 \nonumber\]We already know that \(x>-3\) because \(x\) must be positive, but the other two inequalities do give us new information. The third side must be greater than 3 inches but less than 17 inches long.

Checkpoint \( \PageIndex{ 3 } \)

Can a triangle be made with three wooden sticks of lengths 14 feet, 26 feet, and 10 feet? Sketch a picture, and explain why or why not.

Answer

No, \(10+14\) is not greater than 26.

Types of Triangles

There are three types of triangles classified by whether they have three equal side lengths, two equal side lengths, or no side lengths that are equal. These are called the equilateral, isosceles, and scalene triangles, respectively.

Equilateral Triangles

Definition: Equilateral Triangle

An equilateral triangle has all three sides the same length.

Since all three sides of an equilateral triangle have the same length, there is no smallest side for which the smallest angle will be opposite, and there is no largest side for which the largest angle will be opposite. This gives us the following theorem.

Theorem

All the angles of an equilateral triangle are equal.

Example \( \PageIndex{ 4 } \)

All three sides of a triangle are 4 feet long. Find the angles.

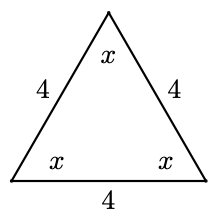
Solution

The triangle is equilateral, so all of its angles are equal. Thus\[\begin{array}{crrclr}
& & 3 x & = & 180 & (\text{Triangle Sum}) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & x & = & 60 & (\text{divide both sides by }3) \\
\end{array} \nonumber \]Each of the angles is \(60^{\circ}\).

Checkpoint \(\PageIndex{4}\)

Find \(x, y\), and \(z\) in the triangle.

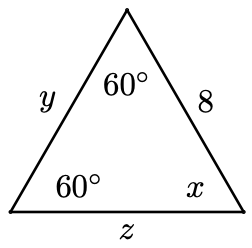
Answer

\(x=60^{\circ}, y=8, z=8\)

Isosceles Triangles

Definition: Isosceles Triangle

An isosceles triangle has two sides of equal length. The angle between the equal sides is the vertex angle, and the other two angles are the base angles.

Theorem

The base angles of an isosceles triangle are equal.

In Example \( \PageIndex{ 5 } \), we introduce another common notation used throughout Geometry - the tick mark. We use tick marks on line segments to denote they have equal length. Similarly, tick marks on angles denote that the angles have the same measure.

Example \(\PageIndex{5}\)

Explain why \(\alpha=\beta\) in the triangle below.

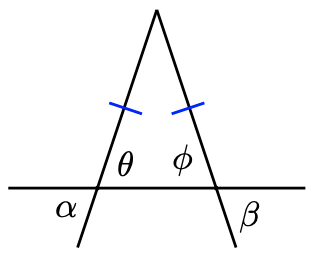
Solution

Because they are the base angles of an isosceles triangle, \(\theta\) (theta) and \(\phi\) (phi) are equal. Also, \(\alpha=\theta\) because they are vertical angles, and similarly \(\beta=\phi\). Therefore, \(\alpha=\beta\) because they are equal to equal quantities.

Example \( \PageIndex{ 6 } \)

Find \(x\) and \(y\) in the triangle.

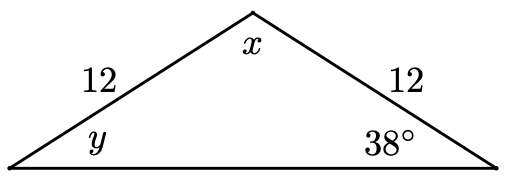
Solution

The triangle is isosceles, so the base angles are equal. Therefore, \(y=38^{\circ}\). To find the vertex angle, we solve\[ \begin{array}{crrclr}
& & x+38+38 & = & 180 & (\text{Triangle Sum}) \\
\scriptscriptstyle\mathrm{Arithmetic} & \implies & x+76 & = & 180 & (\text{add}) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & x & = & 104 & (\text{subtract }76\text{ from both sides}) \\
\end{array} \nonumber \]The vertex angle is \(104^{\circ}\).

Checkpoint \(\PageIndex{6}\)

Find \(x\) and \(y\).

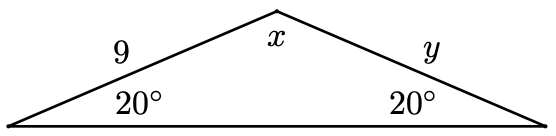
Answer

\(x=140^{\circ}, y=9\)

Scalene Triangles

Finally, we have the scalene triangles.

Definition: Scalene Triangle

A scalene triangle does not have any side lengths or any equal angles.

Figure \( \PageIndex{ 4 } \) shows a general scalene triangle. The different "hash marks" on the sides indicate the side lengths are different. The same is true for the angles.

Figure \( \PageIndex{ 4 } \): A general scalene triangle

Scalene triangles become important in this course when we learn the Law of Sines and the Law of Cosines.

Classification of Triangles by Largest Angle

Most people are not likely to refer to a triangle by its type (equilateral, isosceles, or scalene); however, knowing the features of each type of triangle is important in Trigonometry. Another classification system for triangles, and one that will be referenced constantly in Trigonometry, is based on the size of the triangle's largest angle. Three classifications exist: right, obtuse, and acute triangles.

Obtuse Triangles

We start with the class of triangles having their largest angle greater than \( 90^{ \circ } \).

Definition: Obtuse Triangle

An obtuse triangle is a triangle having an obtuse angle.

Recall that an obtuse angle has measure strictly between \( 90^{ \circ } \) and \( 180^{ \circ } \) (meaning that we exclude \( 90^{ \circ } \) and \( 180^{ \circ } \)). Since the sum of the interior angles of a triangle must be \( 180^{ \circ } \), and one of the angles in an obtuse triangle is greater than \( 90^{ \circ } \), the two smaller angles in an obtuse triangle must sum to strictly less than \( 90^{ \circ } \).

Theorem

In an obtuse triangle, one angle must be greater than \( 90^{ \circ } \), and the remaining two angles must each be less than \( 90^{ \circ } \).

Right Triangles

Reducing the largest possible angle to exactly \( 90^{ \circ } \), we arrive at arguably the most essential triangle classification in Trigonometry - the right triangles.

Definition: Right Triangle

A right triangle is a triangle having a right angle.

Example \( \PageIndex{ 7 } \)

One of the smaller angles of a right triangle is \(34^{\circ}\). What is the third angle?

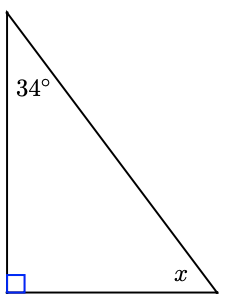
Solution

The sum of the two smaller angles in a right triangle is \(90^{\circ}\). So\[\begin{array}{crrclr}
& & x+34 & = & 90 & \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & x & = & 56 & (\text{subtract }34\text{ from both sides}) \\
\end{array} \nonumber \]The unknown angle must be \(56^{\circ}\).

Checkpoint \(\PageIndex{7}\)

Two angles of a triangle are \(35^{\circ}\) and \(45^{\circ}\). Can it be a right triangle?

Answer

No.

Right Triangles: The Pythagorean Theorem

Arguably, the most important theorem in Trigonometry is the Pythagorean Theorem, mainly because without it, Trigonometry would not exist.

Theorem: Pythagorean Theorem

In a right triangle, if \(c\) stands for the length of the hypotenuse, and the lengths of the two legs are denoted by \(a\) and \(b\) (as shown in the figure below), then\[a^2 + b^2 = c^2. \nonumber \]

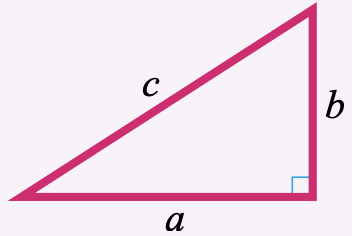
The proof of the Pythagorean Theorem is left as a guided exercise in the homework.

Example \( \PageIndex{ 8 } \)

A 25-foot ladder is placed against a wall so that its foot is 7 feet from the base of the wall. How far up the wall does the ladder reach?

Solution

We sketch the situation, as shown below, and label any known dimensions. We will call the unknown height \(h\).

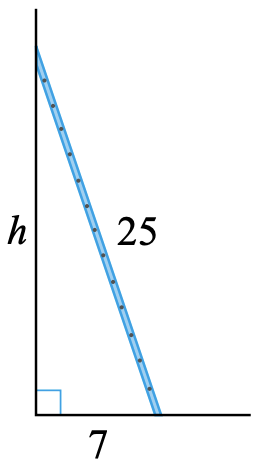
The ladder forms the hypotenuse of a right triangle, so we can apply the Pythagorean Theorem. Substituting 25 for \(c, 7\) for \(b\), and \(h\) for \(a\), we get the following:\[ \begin{array}{rrrclcl}
& & a^2+b^2 & = & c^2 & & \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & h^2+7^2 & = & 25^2 & \quad & \left( \text{substitution} \right)\\
\scriptscriptstyle\mathrm{Arithmetic} & \implies & h^2+49 & = & 625 & \quad & \left( \text{apply powers} \right) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & h^2 & = & 576 & \quad & \left(\text{subtract }49\text{ from both sides}\right) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & h & = & \pm \sqrt{576} & \quad & \left(\text{Extraction of Roots}\right) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & h & = & \pm 24 & \quad & \left(\text{simplify the radical}\right) \\
\end{array} \nonumber \]The height must be a positive number, so the solution \(-24\) does not make sense for this problem. The ladder reaches 24 feet up the wall.

Checkpoint \( \PageIndex{ 8 } \)

A baseball diamond is a square with sides that are 90 feet long. When the catcher sees a runner on first trying to steal second, he throws the ball to the second baseman. Find the straight-line distance from home plate to second base.

Answer

\(90 \sqrt{2} \approx 127.3\) feet

Note

The Pythagorean Theorem is valid only for right triangles, so the converse of the theorem is also true. In other words, if the sides of a triangle satisfy the relationship \(a^2+b^2=c^2\), then the triangle must be a right triangle. We can use this fact to test whether or not a given triangle has a right angle.

Example \( \PageIndex{ 9 } \)

Mike is paving a patio in his backyard and would like to know if the corner at \(C\) is a right angle. He measures 20 cm along one side from the corner and 48 cm along the other, placing pegs \(P\) and \(Q\) at each position, as shown below. The line joining those two pegs is 52 cm long. Is the corner a right angle?

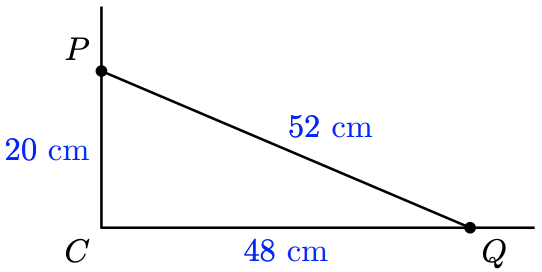
Solution

If it is a right triangle, its sides must satisfy \(p^2+q^2=c^2\). We find\[\begin{array}{rcl}
p^2+q^2 & = & 20^2+48^2 \\
& = & 400+2304 \\
& = & 2704 \\
\end{array} \nonumber \]and\[\begin{array}{rcl}
c^2 & = & 52^2 \\
& = & 2704 \\
\end{array} \nonumber \]Therefore, yes, because \(p^2+q^2=c^2\), the corner at \(C\) is a right angle.

Checkpoint \( \PageIndex{ 9 } \)

The sides of a triangle measure 15, 25, and 30 inches long. Is the triangle a right triangle?

Answer

No

The Pythagorean Theorem relates the sides of right triangles. However, for information about the sides of other triangles, the best we can do (without Trigonometry) is the triangle inequality. Moreover, the Pythagorean Theorem doesn't help us find the angles in a triangle - that comes later.

Acute Triangles

Finally, we reduce the largest possible angle within a triangle to strictly less than \( 90^{ \circ } \) and obtain the acute triangles.

Definition: Acute Triangle

An acute triangle has all interior angles less than \( 90^{ \circ } \).

Special Triangles

We finally arrive at what could be considered the most essential triangles in elementary Trigonometry - the special triangles. These triangles are revered in Trigonometry because they allow the learner (read as "you") to perform computations without needing a calculator. This, in turn, allows the learner to focus on concepts rather than computations.

The \( 30^{ \circ } \)-\( 60^{ \circ } \)-\( 90^{ \circ } \) Triangle

Suppose we have an equilateral triangle with side length \( 2a \), as shown in Figure \( \PageIndex{ 5 } \).

Figure \( \PageIndex{ 5 } \)

Since this triangle is equilateral, each angle is \( 60^{ \circ } \). Drawing an altitude (a line from one vertex to its opposite side, perpendicular to the opposite side) divides the triangle into two smaller triangles. Since the altitude is perpendicular to the base, each of these smaller triangles is a right triangle. Moreover, since one angle in each of these smaller right triangles is \( 60^{ \circ } \), the remaining angle must be \( 30^{ \circ } \) (see Figure \( \PageIndex{ 5 } \)). Furthermore, it can be shown that the side opposite the \( 30^{ \circ } \) angle must have length \( a \) (in the original equilateral triangle, the side opposite \( 60^{ \circ } \) had length \( 2a \), so it should make sense that the side opposite \( 30^{ \circ } \) is half of this). We now look at one of these smaller right triangles (Figure \( \PageIndex{ 6} \) below).

Figure \( \PageIndex{ 6 } \)

This right triangle gains the special distinction of being called a \( 30^{ \circ } \)-\( 60^{ \circ } \)-\( 90^{ \circ } \) triangle. The missing side length, which we will call \( x \) for now, can be found using the Pythagorean Theorem.\[\begin{array}{rrcl}
& x^2 + a^2 & = & (2a)^2 \\
\implies & x^2 + a^2 & = & 4a^2 \\
\implies & x^2 & = & 3a^2 \\
\implies & x & = & a \sqrt{3} \\
\end{array} \nonumber \]

Before we go any further, notice the convention of writing \( x = a \sqrt{3} \) instead of \( x = \sqrt{3} a \). This is purposeful. The latter often leads the reader to think that the \( a \) is "under" the square root. It's good form always to write the radical at the end of a term to avoid this visual ambiguity.

We have successfully derived the following theorem.

Theorem: Side Relationships for a \( 30^{ \circ } \)-\( 60^{ \circ } \)-\( 90^{ \circ } \) Triangle

In any right triangle in which the two acute angles are \( 30^{ \circ } \) and \( 60^{ \circ } \), the hypotenuse is always twice the length of the shortest side (the side opposite the \( 30^{ \circ } \) angle), and the remaining side (opposite the \( 60^{ \circ } \) angle) is always \( \sqrt{3} \) times the shortest side.

Figure \( \PageIndex{ 7 } \)

Example \( \PageIndex{ 10 } \)

Matterhorn Chocolate bars are sold in boxes shaped like triangular prisms. The two triangular ends of a box are equilateral triangles with 8-centimeter sides. When stacking the boxes on a shelf, the second level will be a triangle’s altitude above the bottom level. Find the exact length of the triangle’s altitude, \(h\).

Solution

The altitude divides the triangle into two \(30^{\circ}-60^{\circ}-90^{\circ}\) right triangles, as shown in the figure below.

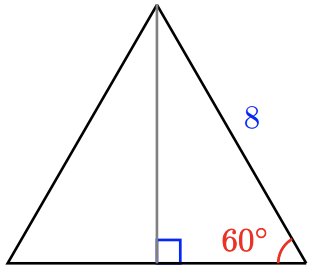
Referring to Figure \( \PageIndex{ 7 } \), we see that the hypotenuse is \( 2a = 8 \), which implies the shortest side (opposite the \( 30^{ \circ } \) angle) is \( a=4 \). Hence, the side opposite the \( 60^{ \circ } \) angle is \( a\sqrt{3} = 4 \sqrt{3} \approx 6.9282 \) centimeters long.

Checkpoint \( \PageIndex{ 10 } \)

A ladder is leaning against a house so that the top is 12 feet above the ground, and the bottom makes a \( 60^{ \circ } \) angle with the ground. Assuming the wall of the house is perpendicular to the ground (and the ground is level), how long is the ladder? State your answer in exact form and round to two decimal places.

Answer

\(\dfrac{24}{\sqrt{3}} \approx 13.86 \) feet

Note that the exact form of the answer in Checkpoint \( \PageIndex{ 10 } \) was left as \( \frac{24}{\sqrt{3}} \). While it is true that you could rationalize the denominator to get\[\dfrac{24}{\sqrt{3}} = \dfrac{24}{\sqrt{3}} \cdot \dfrac{\sqrt{3}}{\sqrt{3}} = \dfrac{24 \sqrt{3}}{3} = 8\sqrt{3}, \nonumber \]we will commonly leave radicals in the denominators of purely numeric expressions.

The \( 45^{ \circ } \)-\( 45^{ \circ } \)-\( 90^{ \circ } \) Triangle

A unique class of isosceles triangle is the isosceles right triangle. This triangle has a right angle, and the two remaining angles are equal. Since the right angle takes \( 90^{ \circ } \), the remaining two angles must share the remaining \( 90^{ \circ } \) evenly. That is, the remaining two angles must be \( 45^{ \circ } \) each. Therefore, the sides opposite these \( 45^{ \circ } \) angles must have the same length. Let \( a \) be the lengths of these legs and \( x \) be the length of the hypotenuse, as shown in Figure \( \PageIndex{ 8 } \).

Figure \( \PageIndex{ 8 } \): The \( 45^{ \circ } \)-\( 45^{ \circ } \)-\( 90^{ \circ } \) triangle

Since this is a right triangle, we can use the Pythagorean Theorem to find the length of the hypotenuse in terms of \( a \).\[\begin{array}{rrcl}
& a^2 + a^2 & = & x^2 \\
\implies & 2 a^2 & = & x^2 \\
\implies & a \sqrt{2} & = & x \\
\end{array} \nonumber \]

Again, notice the convention of writing the radical at the end of the term instead of writing it as \( \sqrt{2} a \).

The gives us the following theorem.

Theorem: Side Relationship for a \( 45^{ \circ } \)-\( 45^{ \circ } \)-\( 90^{ \circ } \) Triangle

In any isosceles right triangle, the hypotenuse is always \( \sqrt{2} \) times the side length.

Example \(\PageIndex{11}\)

You are hired to build a truss to support a balcony. The figure below shows the design plans you have submitted for the project. What is the length of the beam needed from point \( A \) to point \( D \)?

Solution

\( \triangle ABD \) is a \( 45^{ \circ } \)-\( 45^{ \circ } \)-\( 90^{ \circ } \) triangle. Therefore, if the leg length (opposite the \( 45^{ \circ } \) angle) is \( a = 4 \) meters, then beam between points \( A \) and \( D \) must measure \( a\sqrt{2} = 4 \sqrt{2} \approx 5.66 \) meters.

Checkpoint \(\PageIndex{11}\)

Suppose, instead of knowing the 4-meter lengths in Example \( \PageIndex{ 11 } \), we knew that the length of the beam from \( A \) to \( D \) was 12 meters. How long is the beam from \( B \) to \( D \)?

Answer

\( \dfrac{12}{\sqrt{2}} \approx 8.49 \) meters

---

Skills Refresher

The following is a set of review exercises you will need for this section.

Skills Refresher

In Problems 1 - 4, solve the inequality.

1. \(6-x>3\)

2. \(\dfrac{-3 x}{4} \geq-6\)

3. \(3 x-7 \leq-10\)

4. \(4-3 x<2 x+9\)

In Problems 5 - 10, assume that \(x<0\). If this is the case, is the expression positive or negative?

5. \(-x\)

6. \(-(-x)\)

7. \(|x|\)

8. \(-|x|\)

9. \(-|-x|\)

10. \(x^{-1}\)

Answers

1. \(x<3\)

2. \(x \leq 8\)

3. \(x \leq -1\)

4. \(x > -1\)

5. Positive

6. Negative

7. Positive

8. Negative

9. Negative

10. Negative

---

Homework

Vocabulary Check

1. A three-sided polygon is another way of saying ___.

2. If given the triangle \( \triangle ABC \), it is common notation to label the side opposite \( \angle A \) with the letter ___.

3. A triangle where all three sides have the same length is called a ___ triangle.

4. An isosceles triangle has two ___ angles.

5. The ___ angle of an isosceles triangle lies between the two sides of equal length.

6. A(n) ___ triangle must have one angle ___ \( 90^{ \circ } \).

7. A(n) ___ triangle must have all angles ___ \( 90^{ \circ } \).

8. The two special triangles are the ___-\( 90^{ \circ } \) and ___-\( 90^{ \circ } \) triangles.

9. Another name for the \( 45^{ \circ } \)-\( 45^{ \circ } \)-\( 90^{ \circ } \) triangle is a(n) ___ triangle.

Concept Check

10. Is it always true that the hypotenuse is the longest side in a right triangle? Why or why not?

11. In \(\triangle D E F\), is it possible that \(d+e>f\) and \(e+f>d\) are both true? Explain your answer.

12. In a right triangle with hypotenuse \(c\), we know that \(a^2+b^2=c^2\). Is it also true that \(a+b=c\)? Why or why not?

13. Is having more than one obtuse angle in a triangle possible? Why or why not?

14. Draw any quadrilateral (a four-sided polygon) and divide it into two triangles by connecting two opposite vertices by a diagonal. What is the sum of the angles in your quadrilateral?

15. What is the difference between a vertex and vertical angles?

16. In any triangle, the sum of the three angles is ___.

17. The longest side in a triangle is opposite the ___ angle, and the shortest side is opposite the ___ angle.

True or False? For Problems 18 - 24, determine if the statement is true or false. If true, cite the definition or theorem stated in the text supporting your claim. If false, explain why it is false and, if possible, correct the statement.

18. A right triangle always has one angle of \(90^{\circ}\).

19. Given a triangle with side lengths \( a \), \( b \), and \( c \), where \( c \) is the longest side,\[a^2 + b^2 = c^2.\nonumber \]

20. All of the angles of an equilateral triangle are equal.

21. The vertex angles of an isosceles triangle are equal.

22. If the sum of the lengths of any two sides is greater than the length of the third side, then the triangle must be a right triangle.

23. In \( \triangle ABC \), \(a^2 + b^2 = c^2\).

24. If the sides of a triangle satisfy the relationship \(a^2 + b^2 = c^2\), then the triangle is a right triangle.

Basic Skills

For Problems 25 - 30, sketch and label a triangle with the given properties.

25. An isosceles triangle with vertex angle \(30^{\circ}\)

26. A scalene triangle with one obtuse angle

27. A right triangle with legs 4 and 7

28. An isosceles right triangle

29. An isosceles triangle with one obtuse angle

30. A right triangle with one angle \(20^{\circ}\)

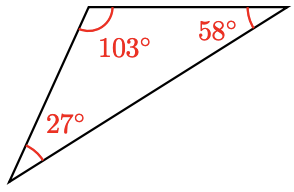
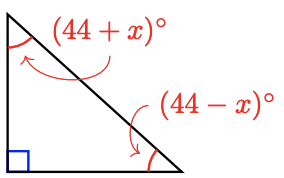
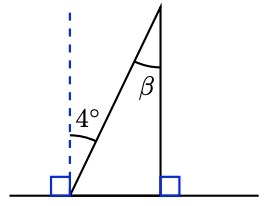
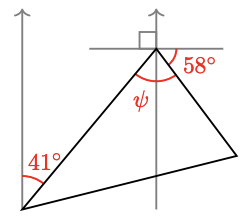
For Problems 31 - 36, find the unknown angle.

31.  

    

32.  

    

33.  

    

34.  

    

35.  

    

36.  

    

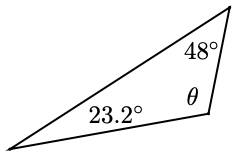
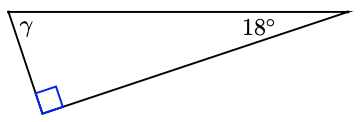
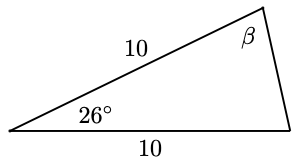
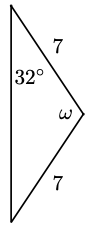
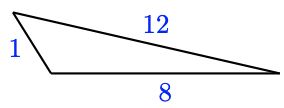
37. If two sides of a triangle are 6 feet and 10 feet long, what are the largest and smallest possible values for the length of the third side?

38. Two adjacent sides of a parallelogram are 3 cm and 4 cm long. What are the largest and smallest possible values for the length of the diagonal?

39. If one of the equal sides of an isosceles triangle is 8 millimeters long, what are the largest and smallest possible values for the length of the base?

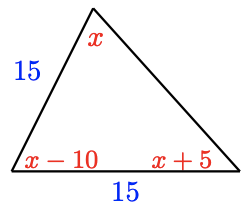
For Problems 40 - 43, find the unknown side of the triangle.

40.  

    

41.  

    

42.  

    

43.  

    

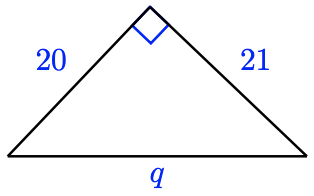
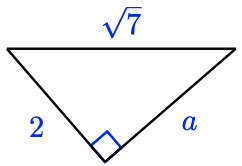
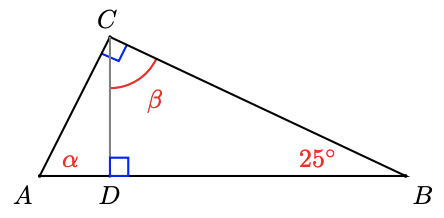
44. Find \(\alpha\) and \(\beta\).

    

     

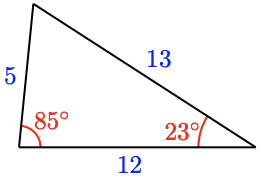
For Problems 45 - 50, decide whether a triangle with the given sides is a right triangle.

45. 9 in, 16 in, 25 in

46. 12 m, 16 m, 20 m

47. 5 m, 12 m, 13 m

48. 5 ft, 8 ft, 13 ft

49. \(5^2\) ft, \(8^2\) ft, \(13^2\) ft

50. \(\sqrt{5}\) ft, \(\sqrt{8}\) ft, \(\sqrt{13}\) ft

Synthesis Questions

51. The two shorter sides of an obtuse triangle are 3 in and 4 in. What are the possible lengths for the third side?

For Problems 52 - 60, explain why the measurements shown cannot be accurate.

52.  

    

53.  

    

54.  

    

55.  

    

56.  

    

57.  

    

58.  

    

59.  

    

60.  

    

For Problems 61 - 68, find the unknown angle. Arrows on a pair of lines indicate that they are parallel.

61.  

    

62.  

    

63.  

    

64.  

    

65.  

    

66.  

    

67.  

    

68.  

    

For Problems 69 - 72, arrows on a pair of lines indicate that they are parallel. Find \(x\) and \(y\).

69.  

    

70.  

    

71.  

    

72.  

    

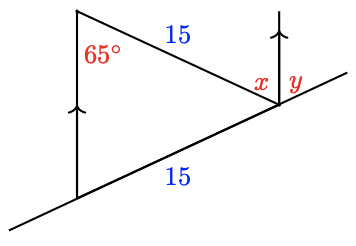
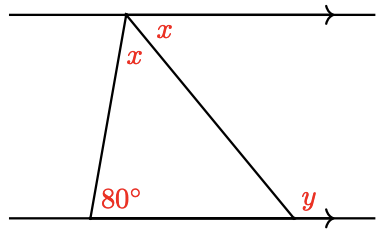
73. How long is the diagonal of a square whose side is 6 centimeters?

74. How long is the side of a cube whose volume is 80 cubic feet?

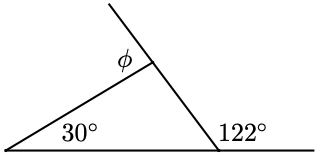
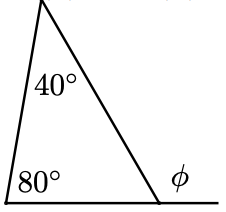
For Problems 75 - 78, the angle labeled \(\phi\) is called an exterior angle of the triangle, formed by one side and the extension of an adjacent side. Find \(\phi\).

75.  

    

76.  

    

77.  

    

78.  

    

For Problems 79 and 80,
(i) Make a sketch of the situation described, and label a right triangle.
(ii) Use the Pythagorean Theorem to solve the problem.

79. The diagonal of a square is 12 inches long. How long is the side of the square?

80. The length of a rectangle is twice its width, and its diagonal is meters long. Find the dimensions of the rectangle.

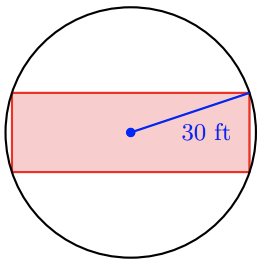
81. What size rectangle can be inscribed in a circle of radius 30 feet if the length of the rectangle must be three times its width?

    

     

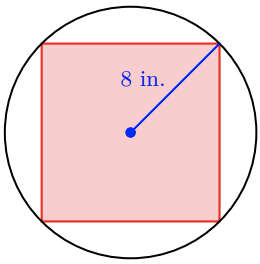
82. What size square can be inscribed inside a circle of radius 8 inches, so that its vertices just touch the circle?

    

     

83. Find \(\alpha, \beta\) and \(h\).

    

     

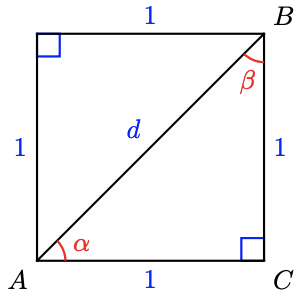
84. Find \(\alpha, \beta\) and \(d\).

    

     

85. Find the diagonal of a cube of side 8 inches. Hint: Find the diagonal of the base first.

    

     

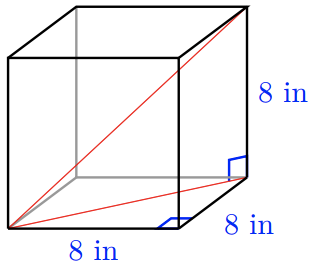
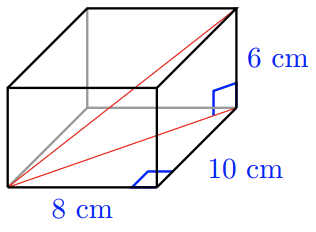
86. Find the diagonal of a rectangular box whose sides are 6 cm by 8 cm by 10 cm. Hint: Find the diagonal of the base first.

    

     

For Problems 87 and 88, \(\Delta ABC\) is equilateral. Find the unknown angles.

87.  

    

88.  

    

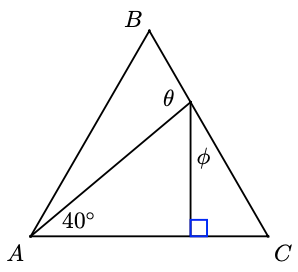
89. Consider the following figure.

    

    1. Compute \(2\theta + 2\phi\).

    2. Compute \(\theta + \phi\).

    3. What must be true about \(\triangle ABC\)?

90. Consider the following figure.

    

     

    1. Explain why \(\angle O A B\) and \(\angle A B O\) are equal in measure.

    2. Explain why \(\angle O B C\) and \(\angle B C O\) are equal in measure.

    3. Explain why \(\angle A B C\) is a right angle.

91.  

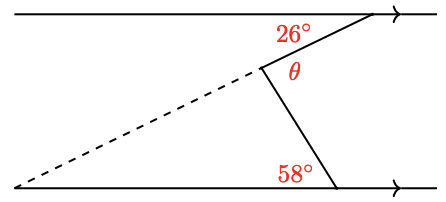
    1. In the figure below, find \(\theta\), and justify your answer.

       

        

    2. Write an algebraic expression for \(\theta\) in the figure below.

       

        

     

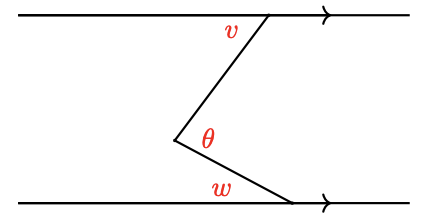
Applications

92. Bounding Distances. The town of Madison is 15 miles from Newton, and 20 miles from Lewis. What are the possible values for the distance from Lewis to Newton?

For Problems 93 and 94,
(i) Make a sketch of the situation described and label a right triangle.
(ii) use the Pythagorean Theorem to solve the problem.

93. TV Dimensions. The size of a TV screen is the length of its diagonal. If the width of a 35-inch TV screen is 28 inches, what is its height?

94. Tree Shadows. If a 30-meter pine tree casts a shadow of 30 meters, how far is the tip of the shadow from the top of the tree?

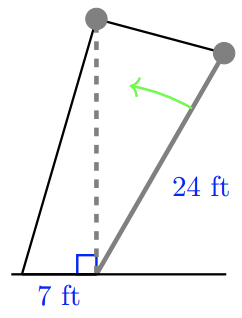
95. A 24-foot flagpole is being raised by a rope and pulley, as shown in the figure. The loose end of the rope can be secured to a ring on the ground 7 feet from the base of the pole. From the ring to the top of the pulley, how long should the rope be when the flagpole is vertical?

     

    

     

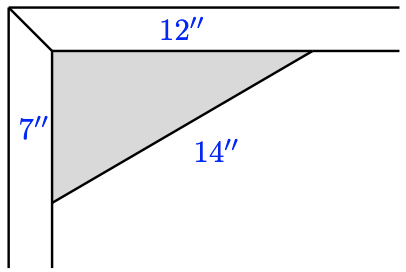
96. To check whether the corners of a frame are square, carpenters sometimes measure the sides of a triangle, with two sides meeting at the join of the boards. Is the corner shown in the figure square?

    

     

For Problems 97 - 99, make a sketch and solve.

97. Pesky Pipe. The back of Ron’s pickup truck is five feet wide and seven feet long. He wants to bring home a 9-foot length of copper pipe. Will it lie flat on the floor of the truck?

98. Pesky Pipe. Mary has a pickup truck with a camper shell. The camper shell floor is five feet wide and seven feet long, but the shell is only three feet tall. Will a 9-foot copper pipe fit diagonally across the back of the truck?

99. What is the longest curtain rod that will fit inside a box 60 inches long by 10 inches wide by 4 inches tall?

Challenge Problems

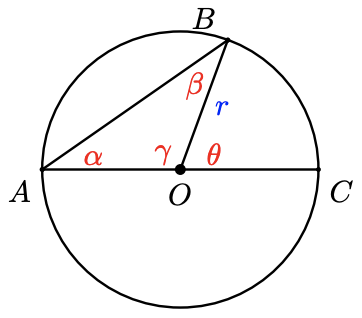
100. Consider the following figure.

     

     1. Compare \(\theta\) with \(\alpha+\beta\). (Hint: What do you know about supplementary angles and the sum of angles in a triangle?

     2. Compare \(\alpha\) and \(\beta\).

     3. Explain why the inscribed angle \(\angle B A O\) is half the size of the central angle \(\angle B O C\).

101. Find an algebraic expression for \(\phi\) and use your answer to write a rule for finding an exterior angle of a triangle.

     

102.  

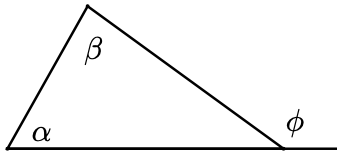
     1. Find the three exterior angles of the triangle. What is the sum of the exterior angles?

        

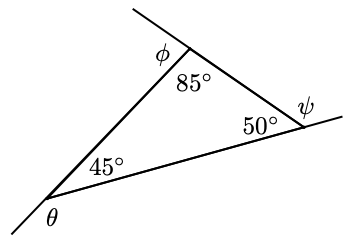
     2. Write an algebraic expression for each exterior angle in terms of one of the angles of the triangle. What is the sum of the exterior angles?

        

         

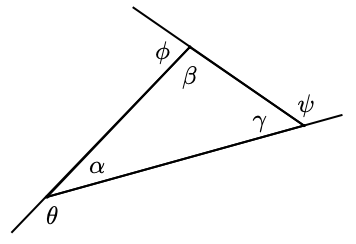
103. Proving the Pythagorean Theorem. There are many proofs of the Pythagorean Theorem. Here is a simple visual argument.

     

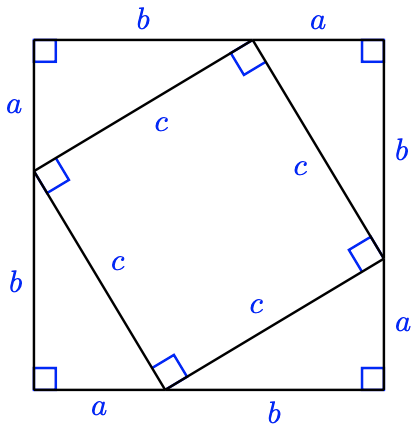
     1. What is the length of the side of the large square in the figure? Write an expression for its area.

     2. Write another expression for the area of the large square by adding the areas of the four right triangles and the smaller central square.

     3. Equate your two expressions for the area of the large square, and deduce the Pythagorean Theorem.

For Problems 104 and 105, the figures inscribed in each problem are regular polygons, which means that all their sides are the same length, and all the angles have the same measure. Find the angles \(\theta\) and \(\phi\).

104.  

     

105.  

     

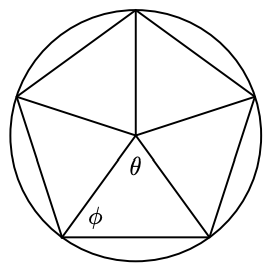
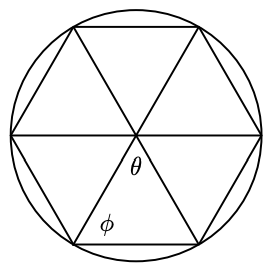
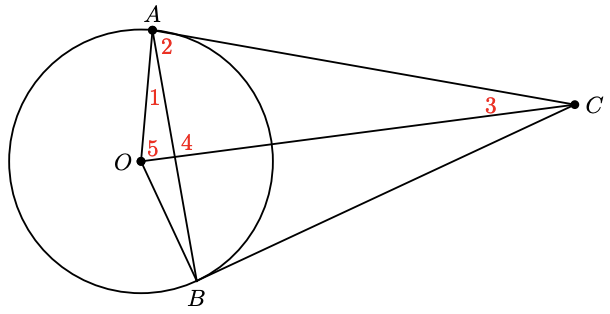
106. A tangent meets the radius of a circle at a right angle. In the figure, \(\angle AOB = 140^{\circ}\). Find the angles labeled 1 through 5 in order, and give a reason for each answer.