1.3: Similar Triangles

Last updated
Save as PDF

Page ID: 146320

Roy Simpson
Cosumnes River College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Determine when two triangles are congruent.
Use proportion to find a side given two similar triangles.
Solve application problems involving similar right triangles.

Congruent Triangles

Two triangles are considered congruent if they have the same size and shape. This means their corresponding angles are equal, and their corresponding sides have the same lengths. For example, it looks as though $ \Delta A B C $ and $ \Delta D E F $ in Figure $ \PageIndex{ 1 } $ are identical in both shape and size ($ \Delta DEF $ has been rotated from $ \Delta ABC $), so they are congruent. We write $ \Delta A B C \cong \Delta D E F $.

$Screen Shot 2022-09-09 at 1.54.27 AM.png$
Figure $ \PageIndex{ 1 } $: Congruent triangles $ \Delta ABC $ and $ \Delta DEF $

Example $ \PageIndex{ 1 } $

The two triangles in the figure below are congruent. List the corresponding parts, and find the angles $\theta$, $\phi$, and $\chi$, and side $z$.

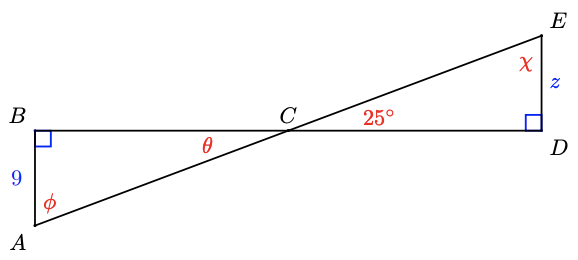
$Screen Shot 2022-09-09 at 1.56.27 AM.png$

Solution: In these triangles, $\angle B=\angle D$ because they are both right angles and $\angle B C A= \angle D C E$ because they are vertical angles, so $\theta=25^{\circ}$. The third angles, $\angle A$ and $\angle E$, must also be equal, so $\phi=\chi=65^{\circ}$. (Do you see why?) The sides opposite each pair of corresponding angles are equal, so $A B=D E, B C=C D$ and $A C=C E$. In particular, we find that $z=9$.

Checkpoint $\PageIndex{1}$

The two triangles in the figure below are congruent. Find the values of $\alpha, \beta$, and $\gamma$.

$Screen Shot 2022-09-09 at 1.58.19 AM.png$

Answer: $ \alpha=85^{\circ}, \beta=75^{\circ}, \gamma=85^{\circ}$

As was mentioned in Section 1.2, the altitude of a triangle is the segment from one vertex of the triangle perpendicular to the opposite side.

Example $ \PageIndex{ 2 } $

Show that the altitude of an equilateral triangle divides it into two congruent right triangles.

Solution

$Screen Shot 2022-09-09 at 2.05.01 AM.png$

Consider, for example, an equilateral triangle of side 8 inches, as shown above. The altitude is perpendicular to the base, so each half of the original triangle is a right triangle. Because each right triangle contains a $60^{\circ}$ angle, the remaining angle in each triangle must be $90^{\circ}-60^{\circ}=30^{\circ}$. Both triangles have a side of length 8 between the angles of $30^{\circ}$ and $60^{\circ}$, so they are congruent. (Consequently, the short sides of the congruent triangles are equal, so each is half the original base.)

Checkpoint $\PageIndex{2}$

The diagonal of a parallelogram divides it into two congruent triangles, as shown in the figure below. List the corresponding parts of the two triangles and explain why each pair is equal.

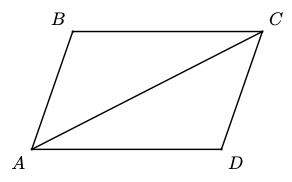
$Screen Shot 2022-09-09 at 2.08.04 AM.png$

Answer: $\angle B C A=\angle C A D$ and $\angle B A C=\angle A C D$ because they are alternate interior angles. If two angles in a triangle are equal, so is the third pair, so $\angle B=\angle D$. $B C=A D$ and $A B=C D$ because they are opposite sides of a parallelogram, and $A C=A C$.

Similar Triangles

The most common comparison of triangles in both Trigonometry and Calculus will be with similar triangles.

Definition: Similar Triangles

Two triangles are similar if they have the same shape but not necessarily the same size.

Similarity between triangles is a weaker form of congruence (the triangles have the same shape but are sized differently); however, this flexibility grants us much power in mathematics.

The corresponding angles between similar triangles are equal, and the corresponding sides are proportional. We can think of one similar triangle as an enlargement or a reduction of the other (see Figure $ \PageIndex{ 2 } $ below).

$Screen Shot 2022-09-09 at 2.12.03 AM.png$
Figure $ \PageIndex{ 2 } $: Proportional relationships between similar triangles

To decide whether two triangles are similar, we must verify only one of the two similarity conditions (the other condition will be true automatically).

Theorem: Similarity Conditions

Two triangles are similar if either

their corresponding angles are equal or
their corresponding sides are proportional.

Example $ \PageIndex{ 3 } $

Which of the pairs of triangles shown below are similar?

$Screen Shot 2022-09-09 at 2.13.32 AM.png$
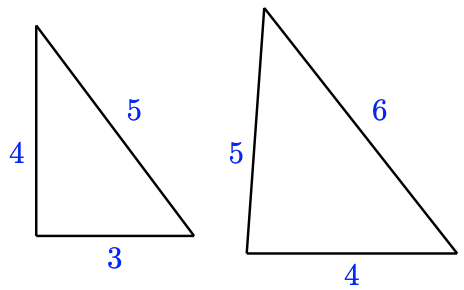
$Screen Shot 2022-09-09 at 2.13.46 AM.png$
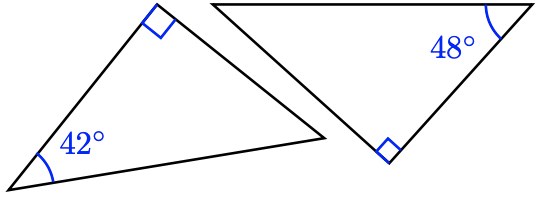
$Screen Shot 2022-09-09 at 2.14.06 AM.png$

Solutions

We will check whether the corresponding sides are proportional. We compute the ratios of the corresponding sides, making sure to write each ratio in the same order, $\frac{\text { larger triangle }}{\text { smaller triangle }}$. (The other order, $\frac{\text { smaller triangle }}{\text { larger triangle }}$, would also work, as long as we use the same order for all the ratios.)\[ \text{shorter legs: }\dfrac{9}{6} \quad \text{longer legs: } \dfrac{12}{8} \quad \text{hypotenuses: } \dfrac{15}{10} \nonumber \]Because all of these ratios are equal to 1.5, the triangles are similar.
The ratios of corresponding sides are not equal: the ratio of the longest sides is $\frac{6}{5}$, but the ratio of the smallest sides is $\frac{4}{3}$. The triangles are not similar.
The missing angle of the first right triangle is $48^{\circ}$, and the missing angle in the second right triangle is $42^{\circ}$, so three pairs of angles match. The triangles are similar.

Checkpoint $\PageIndex{3}$

Are the triangles below similar? Explain why or why not in each case.

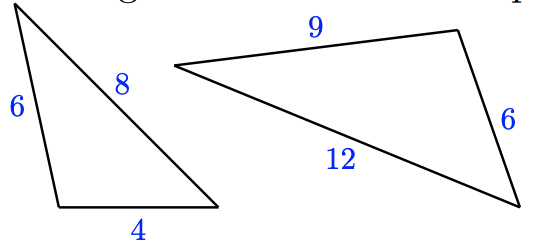
$Screen Shot 2022-09-09 at 2.19.31 AM.png$
$Screen Shot 2022-09-09 at 2.19.55 AM.png$

Answers

The triangles are similar because $\frac{4}{6} = \frac{6}{9} = \frac{8}{12}$, so the sides are proportional.
The third angle in both triangles is $80^{\circ}$, so the triangles are similar because their corresponding angles are equal.^a

In part (b) of Checkpoint $ \PageIndex{ 3 } $, the third angle in each triangle must be $80^{\circ}$ because the sum of the angles is $180^{\circ}$. Thus, we only need to show that two pairs of angles are equal to show that two triangles are similar.

Using Proportions with Similar Triangles

Figure $ \PageIndex{ 3 } $ shows a parallelogram $A B C D$ and two triangles, $\triangle A B E$ and $\triangle F C E$. Can we find the unknown lengths $x$ and $y$ in the larger triangle?

$Screen Shot 2022-09-09 at 2.29.17 AM.png$
Figure $ \PageIndex{ 3 } $

First, note that two pairs of corresponding angles in the triangles are equal: $\angle B E A$ and $\angle F E C$ are vertical angles, and $\angle E F C$ and $\angle B A E$ are alternate interior angles. However, if two pairs of corresponding angles are equal, the third pair must also be equal. This means that the two triangles are similar, and we can use the fact that their corresponding sides are proportional to find $x$ and $y$.

Example $ \PageIndex{ 4 } $

Find the value of $x$ in Figure $ \PageIndex{ 3 } $.

Solution: We see that $x$ is the length of the shortest side in $\triangle A B E$. We know the short side in $\triangle F C E$ and the lengths of the medium sides in each triangle. If we form the ratios of the short and medium sides, we obtain the following proportion.\[\dfrac{\text { larger triangle }}{\text { smaller triangle }}: \dfrac{x}{4}=\dfrac{15}{6} \nonumber\]To solve the proportion, we multiply both sides by the LCD to get\[ \begin{array}{rrrclcl}
& & 6 x & = & 4(15) & \quad & \\
\scriptscriptstyle\mathrm{Arithmetic} & \implies & 6x & = & 60 & \quad & (\text{multiply}) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & x & = & 10 & \quad & (\text{divide both sides by }6) \\
\end{array} \nonumber \]

What does the $ \mathrm{Arithmetic} $ and $ \xcancel{\textrm{Arithmetic}} $ mean?

To get you used to the Mathematical Mantra, every once in a while I will include the "thought processes" during solutions. Just to review, we perform Mathematics in the order we learned it - Arithmetic, Algebra, Trigonometry, $ \ldots $. At each step during a "mechanical" solution process, we should pause and ask ourselves if there is some simple Arithmetic to be done. If not, we move on to any Algebra that can be done. If there is no Algebra to be done, we then move on to Trigonometry.

Thus,

"$ \mathrm{Arithmetic} \implies$" in a solution means that there is some Arithmetic we could do to clean up the previous expression
"$ \xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} \implies$" means there isn't any Arithmetic but there is some Algebra we could use to clean up the previous expression or equation
"$ \xcancel{\mathrm{Arithmetic}} \to \xcancel{\mathrm{Algebra}} \to \mathrm{Trigonometry} \implies$" means there isn't any Arithmetic nor is there any Algebra that can be done to clean up the previous step, so we need to start looking at doing something from Trigonometry.

Checkpoint $\PageIndex{4}$

Find the value of $y$ in the previous example.

Answer: $y=20$

Similar Right Triangles

If two right triangles have one pair of corresponding acute angles with the same measure, they are similar. We can use this fact about right triangles to make indirect measurements.

Example $ \PageIndex{ 5 } $

Ivan wants to know the height of a particular building. He asks Kim to hold up a 5-foot pole near the building and measure the length of its shadow. The shadow of the pole is 3 feet long, and the shadow of the building is 12 feet long.

$Screen Shot 2022-09-09 at 2.35.05 AM.png$

Use similar triangles to write a proportion involving the height of the building.
Solve the proportion to find the height of the building.

Solutions

In the figure above, we see two right triangles: One triangle is formed by the building and its shadow, and the pole and its shadow form the other. Because the light rays from the sun are parallel, the two angles at the tips of the shadows are equal. Thus, the two right triangles are similar, and their corresponding sides are proportional. The ratios of heights and bases in the two triangles yield the proportion\[\dfrac{\text{larger triangle}}{\text{smaller triangle}}: \dfrac{h}{5} = \dfrac{12}{3} \nonumber \]
To solve the proportion, we multiply both sides by the LCD to get\[ \begin{array}{rrrclcl}
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & 3h & = & 5(12) & \quad & \left( \text{multiply both sides by the LCD of all terms in the equation} \right)\\
\scriptscriptstyle\mathrm{Arithmetic} & \implies & 3h & = & 60 & \quad & (\text{multiply}) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & h & = & 20 & \quad & (\text{divide both sides by }3) \\
\end{array} \nonumber \]The building is 20 feet tall.

Checkpoint $\PageIndex{5}$

In Example $ \PageIndex{ 2 } $, we created a $30^{\circ} -60^{\circ} -90^{\circ} $ triangle in which the shorter leg was 4 inches and the hypotenuse was 8 inches. The hypotenuse of another $30^{\circ} -60^{\circ} -90^{\circ} $ triangle is 5 feet. What is the length of the side opposite the $30^{\circ} $ angle?

Answer: $2.5$ feet

Overlapping Triangles

In some applications, similar triangles may share a side or an angle.

Example $ \PageIndex{ 6 } $

Identify two similar triangles in the figure below, and write a proportion to find $H$.

$Screen Shot 2022-09-09 at 2.40.29 AM.png$

Solution

The two triangles overlap, sharing the marked angle, as shown below. Because each triangle also has a right angle, they are similar.

$Screen Shot 2022-09-09 at 2.41.16 AM.png$

Note that the base of the larger triangle is $24 + 12 = 36$. The ratio of the heights and the ratio of the bases must be equal, so we write the following proportion. \[ \begin{array}{rrrclcl}
& & \dfrac{H}{10} & = & \dfrac{36}{24} & \quad & (\text{start with the proportion}) \\
\\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & 24H & = & 360 & \quad & (\text{multiply both sides by the LCD}) \\
\\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & H & = & \dfrac{360}{24} & \quad & (\text{divide both sides by }24) \\
\\
\scriptscriptstyle\mathrm{Arithmetic} & \implies & H & = & 15 & \quad & (\text{division}) \\
\end{array} \nonumber \]

Checkpoint $\PageIndex{6}$

Min wants to know the height of a street lamp. She discovers that when she is 12 feet from the lamp, her shadow is 6 feet long. Find the height of the street lamp.

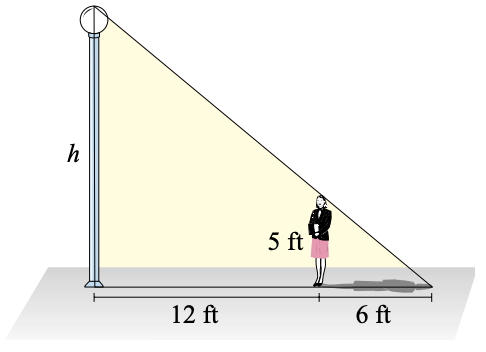
$Screen Shot 2022-09-09 at 2.44.21 AM.png$

Answer: $15$ feet

Skills Refresher

The following is a set of review exercises you will need for this section.

Skills Refresher

In Problems 1 - 5, solve the equation.

$\dfrac{x}{12} = \dfrac{3}{x}$
$1+\dfrac{x}{2} = \dfrac{2x}{5}$
$ \dfrac{x}{6} = \dfrac{1}{6} + \dfrac{x}{6} $
$ x + \dfrac{6}{x} = -5 $
$ \dfrac{5}{2x} = \dfrac{17}{18} - \dfrac{1}{3x} $

Answers

$x = \pm 6$
$x = -10$
$ x = 4 $
$ x = -3 $ and $ x = -2 $
$ x = 3 $

Homework

Vocabulary Check

If given two triangles that are the same size and shape, we say they are ___; however, if their size is different but their shape remains the same, we call them ___ triangles.
The ___ of a triangle is the segment from one vertex of the triangle perpendicular to the ___ side.

Concept Check

What is the difference between congruent triangles and similar triangles?
What is the name of the short-cut method for solving proportions? Why does the method work?
In two triangles, are the triangles similar if two corresponding pairs of angles are equal? How do you know?

True or False? For Problems 6 - 8, determine if the statement is true or false. If true, cite the definition or theorem stated in the text supporting your claim. If false, explain why it is false and, if possible, correct the statement.

The diagonal of a parallelogram splits the shape into two congruent triangles.
In a $ 30^{ \circ } $-$ 60^{ \circ } $-$ 90^{ \circ } $ triangle, the leg opposite the $ 60^{ \circ } $ angle is half the length of the hypotenuse.
If two right triangles have one pair of angles with the same measure, then the triangles are similar.

Basic Skills

For the triangles shown, which of the following equations is true? Explain why.

$Screen Shot 2022-09-09 at 2.54.06 AM.png$
1. $\dfrac{4}{x} = \dfrac{6}{8}$
2. $\dfrac{x}{4} = \dfrac{6}{8}$
3. $\dfrac{x}{x+4} = \dfrac{6}{8}$
4. $\dfrac{x}{x+4} = \dfrac{6}{14}$

For Problems 10 - 13, decide whether the triangles are similar and explain why or why not.

$Screen Shot 2022-09-09 at 4.27.35 PM.png$
$Screen Shot 2022-09-09 at 4.28.00 PM.png$
$Screen Shot 2022-09-09 at 4.28.24 PM.png$
$Screen Shot 2022-09-09 at 4.29.01 PM.png$

Assume the triangles in Problems 14 - 17 are similar. Solve for the variables. (Figures are not drawn to scale.)

$Screen Shot 2022-09-09 at 4.29.45 PM.png$
$Screen Shot 2022-09-09 at 4.30.00 PM.png$
$Screen Shot 2022-09-09 at 4.30.27 PM.png$
$Screen Shot 2022-09-09 at 4.30.37 PM.png$

In Problems 18 - 23, use properties of similar triangles to solve for the variable.

$Screen Shot 2022-09-09 at 4.31.40 PM.png$
$Screen Shot 2022-09-09 at 4.31.51 PM.png$
$Screen Shot 2022-09-09 at 4.32.26 PM.png$
$Screen Shot 2022-09-09 at 4.32.52 PM.png$
$Screen Shot 2022-09-09 at 4.33.01 PM.png$
$Screen Shot 2022-09-09 at 4.33.11 PM.png$

For Problems 24 - 29, use properties of similar triangles to solve for the variable.

$Screen Shot 2022-09-09 at 4.42.48 PM.png$
$Screen Shot 2022-09-09 at 4.42.57 PM.png$
$Screen Shot 2022-09-09 at 4.43.07 PM.png$
$Screen Shot 2022-09-09 at 4.43.16 PM.png$
$Screen Shot 2022-09-09 at 4.43.27 PM.png$
$Screen Shot 2022-09-09 at 4.43.36 PM.png$

Synthesis Questions

In Problems 30 - 33, name two congruent triangles and find the unknown quantities.

$P QRS$ is an isosceles trapezoid.

$Screen Shot 2022-09-09 at 3.01.36 AM.png$
$Screen Shot 2022-09-09 at 3.02.06 AM.png$
$\Delta PRU$ is isosceles.

$Screen Shot 2022-09-09 at 4.19.28 PM.png$
$\Delta P RU$ is isosceles and $OR = NG$. Find $\angle RNG$ and $\angle RNO$.

$Screen Shot 2022-09-09 at 4.21.37 PM.png$

For Problems 34 - 36, explain why the measurements shown are inaccurate.

$Screen Shot 2022-09-11 at 6.33.56 PM.png$
$Screen Shot 2022-09-11 at 6.34.26 PM.png$
$Screen Shot 2022-09-11 at 6.35.48 PM.png$
The follow pairs of triangles are similar. Solve for $y$ in terms of $x$.
$Screen Shot 2022-09-09 at 4.41.40 PM.png$

In Problems 38 - 41, solve for $y$ in terms of $x$.

$Screen Shot 2022-09-09 at 4.45.09 PM.png$
$Screen Shot 2022-09-09 at 4.45.18 PM.png$
$Screen Shot 2022-09-09 at 4.45.29 PM.png$
$Screen Shot 2022-09-09 at 4.45.39 PM.png$
Triangle $ABC$ is a right triangle, and $AD$ meets the hypotenuse $BC$ at a right angle.

$Screen Shot 2022-09-09 at 4.47.57 PM.png$
1. If $\angle ACB = 20^{\circ}$, find $\angle B$, $\angle CAD$, and $\angle DAB$.
2. Find two triangles similar to $\Delta ABC$. List the corresponding sides in each of the triangles.

Applications

Measuring Distances. Ivan and Kim want to measure the distance across a stream. They mark point $A$ directly across the stream from a tree at point $T$ on the opposite bank. Ivan walks from point $A$ down the bank a short distance to point $B$ and sights the tree. He measures the angle between his line of sight and the stream bank.
1. Draw a figure showing the stream, the tree, and the right triangle $\triangle ABT$.
2. Meanwhile, Kim, still standing at point $A$, walks away from the stream at right angles to Ivan’s path. Ivan watches her progress and tells her to stop at point $C$ when the angle between the stream bank and his line of sight to Kim is the same as the angle from the stream bank to the tree. Add triangle $\triangle ABC$ to your figure.
3. Ivan now measures the distance from point $A$ to Kim at point $C$. Explain why this distance is the same as the distance across the stream.
Measuring Distances. If you have a baseball cap, here is another way to measure the distance across a river. Stand at point $A$ directly across the river from a convenient landmark, say a large rock, on the other side. Tilt your head down so that the brim of the cap points directly at the base of the rock, $R$.
1. Draw a figure showing the river, the rock, and the right triangle $\triangle ABR$, where $B$ is the location of your baseball cap on your head.
2. Now, without changing the angle of your head, rotate $90^{\circ}$ and sight along the bank on your side of the river. Have a friend mark the spot $C$ on the ground where the brim of your cap points. Add triangle $\triangle ABC$ to your figure.
3. Finally, you can measure the distance from point $A$ to point $C$. Explain why this distance is the same as the distance across the river.

For Problems 45 - 50, use properties of similar triangles to solve.

Heights. A rock climber estimates the height of a cliff she plans to scale. She places a mirror on the ground to see the top of the cliff in the mirror while she stands straight. The angles 1 and 2 formed by the light rays are equal, as shown in the figure. She then measures the distance to the mirror (2 feet) and the distance from the mirror to the base of the cliff (56 feet). How high is the cliff if she is 5 feet 6 inches tall?

$Screen Shot 2022-09-09 at 4.35.13 PM.png$
Heights. Lap wants to estimate the height of the Washington Monument. He notices that he can see the reflection of the top of the monument in the reflecting pool. He is 35 feet from the tip of the reflection, and that point is 1080 yards from the base of the monument, as shown below. From his physics class, Lap knows that the angles marked (in the image below) are equal. If Lap is 6 feet tall, what is his estimate for the height of the Washington Monument?

$Screen Shot 2022-09-09 at 4.36.48 PM.png$
Distances. In the sixth century BC, the Greek philosopher and mathematician Thales used similar triangles to measure the distance to a ship at sea. Two observers on the shore at points $A$ and $B$ would sight the ship and measure the angles formed, as shown in Figure (a). They would then construct a similar triangle, as shown in Figure (b), with the same angles at $A$ and $B$, and measure its sides. (This method is called triangulation.) Use the lengths given in the figures to find the distance from the observer at location $B$ to the ship.

$Screen Shot 2022-09-09 at 4.37.49 PM.png$
Distances. The Capilano Suspension Bridge is a footbridge that spans a 230-foot gorge north of Vancouver, British Columbia. Before crossing the bridge, you decide to estimate its length. You walk 100 feet downstream from the bridge and sight its far end, noting the angle formed by your line of sight, as shown in Figure (a). You then construct a similar right triangle with a two-centimeter base, as shown in Figure (b). You find that the height of your triangle is 8.98 centimeters. How long is the Capilano Suspension Bridge?

$Screen Shot 2022-09-09 at 4.38.44 PM.png$
Surface Area. A conical tank is 12 feet deep, and the top's diameter is 8 feet. If the tank is filled with water to a depth of 7 feet, as shown in the figure at right, what is the area of the exposed surface of the water?

$Screen Shot 2022-09-09 at 4.39.28 PM.png$
Distances. To measure the distance $EC$ across the lake shown in the figure at right, stand at $A$ and sight point $C$ across the lake, then mark point $B$. Then sight to point $E$ and mark point $D$ so that $DB$ is parallel to $EC$. If $AD = 25$ yards, $AE = 60$ yards, and $BD = 30$ yards, how wide is the lake?

$Screen Shot 2022-09-09 at 4.41.01 PM.png$

Challenge Problems

Distances. Here is a way to find the distance across a gorge using a carpenter’s square and a five-foot pole. Plant the pole vertically on one side of the gorge at point $A$ and place the angle of the carpenter’s square on top of the pole at point $B$, as shown in the figure. Sight along one side of the square so that it points to the opposite side of the gorge at point $P$. Without moving the square, sight along the other side and mark point $Q$. If the distance from $Q$ to $A$ is six inches, calculate the width of the gorge. Explain your method.

$Screen Shot 2022-09-09 at 4.49.53 PM.png$

Search

Text Color

Text Size

Margin Size

Font Type

Example \( \PageIndex{ 1 } \)

Checkpoint \(\PageIndex{1}\)

Example \( \PageIndex{ 2 } \)

Checkpoint \(\PageIndex{2}\)