1.4: Lines, Circles, and Angles in the Rectangular Coordinate System

Suggested Prerequisite Topics

Technically, most of the material in this section is prerequisite for this course; however, it's so important for your success in Trigonometry that we include it as its own section. Material not explicitly covered in this section, but needed as prerequisite for this section includes the following:

• Number systems (specifically, integers) and number set notation (again, specifically, the integers)
• Simplifying fractional expressions
• Understanding the meaning of "Undefined"
• Cartesian Coordinate System
• Graphing equations of lines
• Intercepts (of lines)
• Understanding the link between the solution set of an equation in two variables and the "graph of the equation"

Learning Objectives

• Calculate the slope of the line connecting two points.
• Interpret the meaning of slope in applications.
• Determine the equation of a line containing two given points.
• Graph a line given its equation.
• Construct a linear model that can be used to extrapolate values.
• Compute the distance between two points on the Cartesian plane.
• Verify a point lies on the unit circle.
• Graph a circle given its equation.
• Determine in which quadrant an angle in standard position terminates.
• Sketch an angle in standard position.
• Find an angle coterminal with a given angle.

Lines

Slopes and Rates of Change

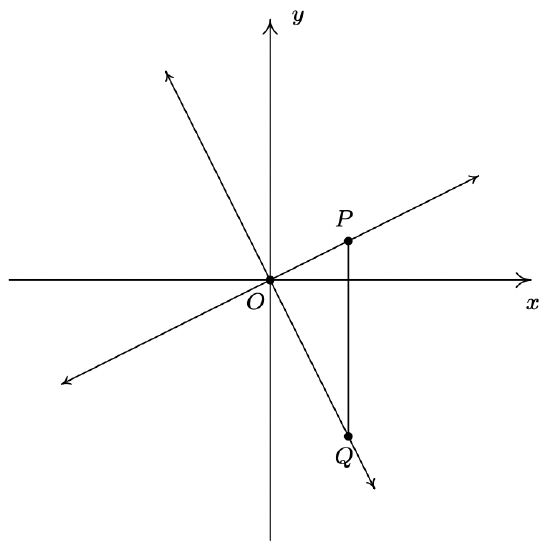
Recall from Geometry that two distinct points in the Cartesian coordinate plane (also known as the Cartesian coordinate system or the rectangular coordinate system) determine a unique line containing those points (see Figure \( \PageIndex{ 1 } \) below).

Figure \( \PageIndex{ 1 } \): A line defined by two distinct points on the plane

To give a sense of the "steepness" of the line, we recall that we can compute the slope of the line.

Definition: Slope

The slope \(m\) of the line containing the points \(P\left(x_{0}, y_{0}\right)\) and \(Q\left(x_{1}, y_{1}\right)\) is\[ m=\dfrac{y_{1}-y_{0}}{x_{1}-x_{0}}, \label{SlopeFormula} \]provided \(x_{1} \neq x_{0}\).

A couple of notes are in order. First, don’t ask why we use the letter \(m\) to represent slope. There are many explanations, but apparently, no one knows for sure. Secondly, the stipulation \(x_{1} \neq x_{0}\) ensures that we aren’t trying to divide by zero.

Example \( \PageIndex{1} \)

Find the slope of the line containing the following pairs of points, if it exists. Plot each pair of points and the line containing them.

1. \(P(-1,2), \quad Q(3,4)\)
2. \(P(-2,3), \quad Q(2,-3)\)
3. \(P(-3,2), \quad Q(4,2)\)
4. \(P(2,3), \quad Q(2,-1)\)

Solutions

1. \(m=\dfrac{4-2}{3-(-1)}=\dfrac{2}{4}=\dfrac{1}{2}\)

   

2. \(m=\dfrac{-3-3}{2-(-2)}=\dfrac{-6}{4}=-\dfrac{3}{2}\)

   

3. \(m=\dfrac{2-2}{4-(-3)}=\dfrac{0}{7}=0\)

   

4. \(m=\dfrac{-1-3}{2-2}=\dfrac{-4}{0}\), which is undefined

   

Checkpoint \(\PageIndex{1}\)

Find the slope of the line containing the points \(P(0,0)\) and \(Q(2,4)\), if it exists. Plot the pair of points and the line containing them.

Answer

\(m=2\)

A few comments about Example \( \PageIndex{1} \) are in order. First, for reasons which will be made clear soon, if the slope is positive then the resulting line is said to be increasing. If it is negative, we say the line is decreasing. A slope of 0 results in a horizontal line which we say is constant, and an undefined slope results in a vertical line.

Second, the larger the slope (in absolute value), the steeper the line. You may recall from Algebra that slope can be described as the ratio \[\dfrac{\text {rise}}{\text {run}}.\nonumber\]For example, in Example \( \PageIndex{1a} \), we found the slope to be \( \frac{1}{2} \). We can interpret this as a rise of 1 unit upward for every 2 units to the right we travel along the line, as shown in Figure \( \PageIndex{ 2 } \) below.

Figure \( \PageIndex{ 2 } \)

The interpretation of slope as "rise over run" gives us a better understanding of why we say a line is increasing when its slope is positive - it is rising a certain number of units when we "run" a certain number of units. Likewise, a negative slope resulting in a decreasing line should be obvious - the line is falling a certain number of units when we "run" a certain number of units.

Using more formal notation, given points \(\left(x_{0}, y_{0}\right)\) and \(\left(x_{1}, y_{1}\right)\), we use the Greek letter Delta, \(\Delta\), to write \(\Delta y = y_{1}-y_{0}\) and \(\Delta x = x_{1}-x_{0}\). In most scientific circles, the symbol \(\Delta\) means "change in." Hence, we may write\[m=\dfrac{\Delta y}{\Delta x}, \nonumber \]which describes the slope as the rate of change of \(y\) with respect to \(x\). Rates of change abound in the "real world," as the next example illustrates.

Example \( \PageIndex{2} \)

Suppose two separate temperature readings were taken at the ranger station on the top of Mt. Sasquatch. At 6 A.M., the temperature was \(24^{\circ} \mathrm{F}\) and at 10 A.M. it was \(32^{\circ} \mathrm{F}\).

1. Find the slope of the line containing the points \((6, 24)\) and \((10, 32)\).
2. Interpret your answer to the first part in terms of temperature and time.
3. Predict the temperature at noon.

Solutions

1. For the slope, we have \(m=\frac{32-24}{10-6}=\frac{8}{4}=2\).
2. Since the values in the numerator correspond to the temperatures in \({ }^{\circ} \mathrm{F}\), and the values in the denominator correspond to time in hours, we can interpret the slope as \(2=\frac{2}{1}=\frac{2^{\circ} \mathrm{F}}{1 \text { hour }}\), or \(2^{\circ} \mathrm{F}\) per hour. Since the slope is positive, we know this corresponds to an increasing line. Hence, the temperature is increasing at a rate of \(2^{\circ} \mathrm{F}\) per hour.
3. Noon is two hours after 10 AM. Assuming a temperature increase of \(2^{\circ} \mathrm{F}\) per hour, in two hours, the temperature should rise \(4^{\circ} \mathrm{F}\). Since the temperature at 10 AM is \(32^{\circ} \mathrm{F}\), we would expect the temperature at noon to be \(32+4=36^{\circ} \mathrm{F}\).

It may well happen that in the previous scenario, at noon, the temperature is only \(33^{\circ} \mathrm{F}\). This doesn’t mean our calculations are incorrect; instead, it means that the temperature change throughout the day isn’t a constant \(2^{\circ} \mathrm{F}\) per hour. Mathematical models are just that: models. The predictions we get from the models may be mathematically accurate but not resemble what happens in the real world.

Checkpoint \(\PageIndex{2}\)

Lap is writing a textbook for his math students. He writes around 1251 words every three days. How many words has he written by the end of the sixth day? What about by the end of the ninth day? How many words does he write per day?

Answer

\( 2502 \) words by the end of the sixth day, \( 3753 \) words by the end of the ninth day, and \( m = \frac{3753 - 2502}{9 - 6} = 417 \) words per day.

Equations of Lines

Suppose a line has a slope of \(m\) and contains the point \(\left(x_{0}, y_{0}\right)\). Suppose \((x, y)\) is another point on the line, as indicated in Figure \( \PageIndex{ 3 } \) below.

Figure \( \PageIndex{ 3 } \)

Equation \( \ref{SlopeFormula} \) yields\[\begin{array}{rrcl}
& m & = & \dfrac{y-y_{0}}{x-x_{0}} \\
\\
\implies & m \left(x-x_{0}\right) & = & y-y_{0} \\
\\
\implies & y-y_{0} & = & m\left(x-x_{0}\right) \\
\end{array}\nonumber\]We have just derived the point-slope form of a line.

Definition: Point-Slope Form of a Line

The point-slope form of the line with slope \(m\) containing the point \(\left(x_{0}, y_{0}\right)\) is the equation\[ y-y_{0}=m\left(x-x_{0}\right). \label{PointSlopeForm} \]

Concept: Lines Have Constant Slope

It is essential to understand that the slope of a line is constant. That is, the slope between any two points on a line is the same.

Example \( \PageIndex{3} \)

Write the equation of the line containing the points \((−1, 3)\) and \((2, 1)\).

Solution

In order to use Equation \( \ref{PointSlopeForm} \), we need to find the slope of the line in question. Hence, we use Equation \( \ref{SlopeFormula} \) to get\[ m=\dfrac{\Delta y}{\Delta x}=\dfrac{1-3}{2-(-1)}=-\dfrac{2}{3}. \nonumber \]We are spoiled for choice for a point \(\left(x_{0}, y_{0}\right)\). We’ll use \((−1, 3)\) and leave it to the reader to check that using \((2, 1)\) results in the same equation. Substituting into the point-slope form of the line, we get\[\begin{array}{rrrclcl}
& & y-y_{0} & = & m\left(x-x_{0}\right) & \quad & (\text{Point-Slope Form}) \\
\\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & y-3 & = & -\dfrac{2}{3}(x-(-1)) & \quad & (\text{substitute in known values}) \\
\\
\scriptscriptstyle\mathrm{Arithmetic} & \implies & y-3 & = & -\dfrac{2}{3}(x+1) & \quad & \left( \text{multiplication} \right) \\
\\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & y-3 & = & -\dfrac{2}{3} x-\dfrac{2}{3} & \quad & (\text{distribute}) \\
\\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to  \mathrm{Algebra} & \implies & y & = & -\dfrac{2}{3} x+\dfrac{7}{3} & \quad & (\text{add }3\text{ to both sides}) \\
\end{array}\nonumber \]We can check our answer by showing that both \((−1, 3)\) and \((2, 1)\) are on the graph of \(y=-\frac{2}{3} x+\frac{7}{3}\) algebraically.

What does the \( \mathrm{Arithmetic} \) and \( \xcancel{\textrm{Arithmetic}} \) mean?

To get you used to the Mathematical Mantra, every once in a while I will include the "thought processes" during solutions. Just to review, we perform Mathematics in the order we learned it - Arithmetic, Algebra, Trigonometry, \( \ldots \). At each step during a "mechanical" solution process, we should pause and ask ourselves if there is some simple Arithmetic to be done. If not, we move on to any Algebra that can be done. If there is no Algebra to be done, we then move on to Trigonometry.

Thus,

• "\( \mathrm{Arithmetic} \implies\)" in a solution means that there is some Arithmetic we could do to clean up the previous expression
• "\( \xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} \implies\)" means there isn't any Arithmetic but there is some Algebra we could use to clean up the previous expression or equation
• "\( \xcancel{\mathrm{Arithmetic}} \to \xcancel{\mathrm{Algebra}} \to \mathrm{Trigonometry} \implies\)" means there isn't any Arithmetic nor is there any Algebra that can be done to clean up the previous step, so we need to start looking at doing something from Trigonometry.

Checkpoint \(\PageIndex{3}\)

Find the equation of the line going through the points \( \left(\frac{1}{2}, 7\right) \) and \( \left( -2, \frac{4}{3} \right) \).

Answer

\( y = \dfrac{34}{15}x + \dfrac{88}{15} \)

In simplifying the equation of the line in Example \( \PageIndex{ 3 } \), we produced another form of a line, the slope-intercept form. This is the familiar \(y = mx + b\) form you have seen in Algebra. The "intercept" in "slope-intercept" comes from the fact that if we set \(x = 0\), we get \(y = b\). In other words, the \(y\)-intercept of the line \(y = mx + b\) is \((0, b)\).

Definition: Slope-Intercept Form of a Line

The slope-intercept form of the line with slope \(m\) and y-intercept \((0, b)\) is the equation\[y = mx + b. \label{SlopeInterceptForm} \]

Note that if we have slope \(m = 0\) in Equation \( \ref{SlopeInterceptForm} \), we get the equation \(y = b\), which is the formula for a horizontal line.

Concept: The Initial Value of a Function

In mathematical models, the \( y \)-intercept (also known as the vertical intercept) is called the initial value of the function.

Graphs of Lines

The graph of \( y = mx + b \) is a line with slope \(m\) and \(y\)-intercept \((0, b)\). Moreover, the graph of \( y=b \) is a horizontal line (a line with slope \(m = 0\)) and a \(y\)-intercept of \((0, b)\).

Example \( \PageIndex{4} \)

Graph the following equations. If the graph is a line, identify the slope and \(y\)-intercept.

1. \(y = 3\)
2. \(y = 3x − 1\)
3. \(y=\frac{x^{2}-4}{x-2}\)

Solutions

1. The graph of \(y = 3\) is a horizontal line (\(m = 0\)) through \((0, 3)\) (see the figure below).

   

2. Comparison of this equation with Equation \( \ref{SlopeInterceptForm} \) yields \(m = 3\) and \(b = −1\). Hence, our slope is \(3\) and our \(y\)-intercept is \((0, −1)\). To get another point on the line, we can choose \( x=1 \) to get that \( y = 2 \).

   

3. If we simplify the right side of the equation, we get\[ y = \dfrac{x^{2}-4}{x-2} = \dfrac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}} = x+2. \nonumber \]However, if we were to state \(y = x + 2\), we would be committing a sin of omission. In this case, \(y\) has big problems when \(x = 2\) and, as such, \( x = 2 \) is not an allowable "input" value. In terms of functions, the domain of \(y = f(x)\) is \( (-\infty, 2) \cup (2, \infty)\). To indicate this, we write \(y = x + 2\), \(x \neq 2\). Therefore, except at \(x = 2\), we graph the line \(y = x + 2\). The slope is \(m = 1\) and the \(y\)-intercept is \((0, 2)\). A second point on the graph is \((1, 3)\). Since the equation is not defined at \(x = 2\), we put an open circle at the point that would be on the line \(y = x + 2\) when \(x = 2\), namely \((2, 4)\) (see the figure below).

   

Checkpoint \(\PageIndex{4}\)

Graph \(y=\frac{3-2 x}{4}\), and state the slope and \( y \)-intercept.

Answer

\(m=-\frac{1}{2}\) and \(b=\frac{3}{4}\).

Example \( \PageIndex{4c} \) and Checkpoint \( \PageIndex{ 4 } \) showcase some of the difficulties in defining a line using the phrase "of the form." It would be incorrect to define a line as "the graph of an equation of the form \( y=mx + b \)." Some algebraic manipulations may be needed to rewrite a given equation to match "the form."

Horizontal and vertical lines play an essential role in Trigonometry, so formalizing their equations is worthwhile.

Theorem: Equations of Horizontal and Vertical Lines

The horizontal line containing the point \( \left( k,c \right) \), where \( k \) is any real number, is\[ y = c. \nonumber \]The vertical line containing the point \( \left( c, k \right) \), where \( k \) is any real number, is\[ x = c. \nonumber \]

The Distance Formula

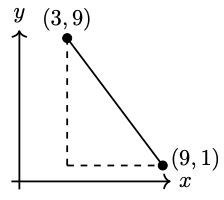
Matt is hiking in the Santa Monica mountains. He would like to know the distance from the Sycamore Canyon trailhead, located at \(12-\mathrm{C}\) on his map, to the Coyote Trail junction, located at \(8-\mathrm{F}\), as shown below.

Each interval on the map represents one kilometer. Matt remembers the Pythagorean Theorem and uses the map coordinates to label the sides of a right triangle. The distance he wants is the hypotenuse of the triangle, so\[\begin{array}{rrcl}
& d^2 & = & 4^2+3^2 \\
\implies & d^2 & = & 16 + 9 \\
\implies & d^2 & = & 25 \\
\implies & d & = & \sqrt{25} \\
\implies & d & = & 5 \\
\end{array} \nonumber \]The straight-line distance to Coyote junction is about 5 kilometers. The formula for the distance between two points is obtained similarly.

We first label a right triangle with points \(P_1\) and \(P_2\) on opposite ends of the hypotenuse (see Figure \( \PageIndex{ 4 } \)). The sides of the triangle have lengths \(|x_2 - x_1|\) and \(|y_2 - y_1|\). We can use the Pythagorean Theorem to calculate the distance between \(P_1\) and \(P_2\):

\(d^2 = (x_2-x_1)^2 + (y_2 - y_1)^2\)

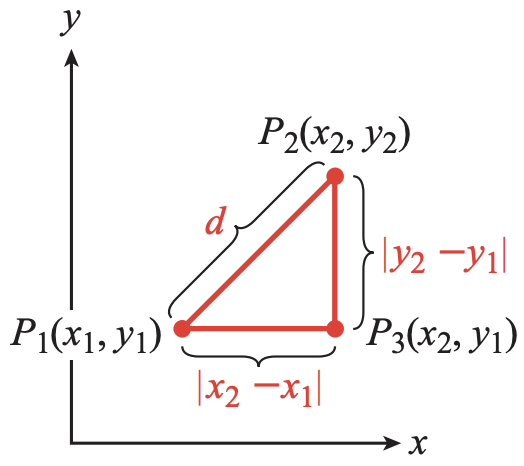
Figure \( \PageIndex{ 4 } \)

Taking the (positive) square root of each side of this equation gives us the Distance Formula.

Theorem: Distance Formula

The distance \(d\) between two points \(P_1\left(x_1, y_1\right)\) and \(P_2\left(x_2, y_2\right)\) is\[d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \nonumber\]

Example \( \PageIndex{ 5 } \)

Find the distance between (2, −1) and (4, 3).

Solution

We substitute \((2,-1)\) for \(\left(x_1, y_1\right)\) and \((4,3)\) for \(\left(x_2, y_2\right)\) in the Distance Formula to obtain

\[\begin{array}{rrrclcl}
& & d &=&\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} & \quad & \left( \text{Distance Formula} \right) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra}&\implies & & = & \sqrt{(4-2)^2+[3-(-1)]^2} & \quad & \left( \text{substitution} \right)\\
\scriptscriptstyle\mathrm{Arithmetic}&\implies & & = & \sqrt{2^2+4^2} & \quad & \left( \text{addition and subtraction} \right) \\
\scriptscriptstyle\mathrm{Arithmetic}&\implies & & = & \sqrt{4 + 16} & \quad & \left( \text{applying powers} \right) \\
\scriptscriptstyle\mathrm{Arithmetic}&\implies & & = & \sqrt{20} & \quad & \left( \text{addition} \right) \\
\scriptscriptstyle\mathrm{Arithmetic}&\implies & & = & 2 \sqrt{5} & \quad & \left( \text{simplify the radical} \right)
\end{array} \nonumber \]The exact value of the distance, shown at right, is \(2 \sqrt{5}\) units. We obtain the same answer if we use \((4,3)\) for \(P_1\) and \((2,-1)\) for \(P_2\):

\begin{aligned}
d &=\sqrt{(2-4)^2+[(-1)-3]^2} \\
&=\sqrt{4+16}=\sqrt{20}=2 \sqrt{5}
\end{aligned}

We can use a calculator to obtain an approximation for this value and find

\[2 \sqrt{5} \approx 2(2.236)=4.472 \nonumber\]

Critical Mistake

In Example \( \PageIndex{ 5 } \), the radical \(\sqrt{4+16}\) cannot be simplified to \(\sqrt{4}+\sqrt{16}\). (Do you remember why not?)

Checkpoint \( \PageIndex{ 5 } \)

1. Find the distance between the points (−5, 3) and (3, −9).
2. Plot the points on a Cartesian coordinate system and show how the Pythagorean Theorem is used to calculate the distance.

Answers

1. \(4\sqrt{13}\)
2. The points (−5, 3) and (3, −9) are two vertices of a right triangle with one horizontal leg of length 8 and one vertical leg of length 12. The distance between (−5, 3) and (3, −9) is the hypotenuse \(c\).
   

Equation for a Circle

We can use the Distance Formula to find an equation for a circle. The circle shown in Figure \( \PageIndex{ 5 } \) has its center at the origin, (0, 0), and its radius is \(r\).

Figure \( \PageIndex{ 5 } \): The circle of radius \( r \) centered at the origin.

The distance from the origin to any point \(P(x, y)\) on the circle is \(r\). Therefore,\[\sqrt{(x-0)^2+(y-0)^2} = r\nonumber \]or, squaring both sides,\[(x-0)^2 + (y-0)^2 = r^2\nonumber \]Because every point on the circle must satisfy this equation, we have found an equation for the circle.

Theorem: Equation of a Circle with Radius \( r \) Centered at the Origin

The equation for a circle of radius \(r\) centered at the origin is\[x^2 + y^2 = r^2\nonumber \]

Example \( \PageIndex{ 6 } \)

Find two points on the circle \(x^2+y^2=4\) with an \(x\)-coordinate of \(-1\).

Solution

We substitute \(x=-1\) into the equation for the circle and solve for \(y\).\[\begin{array}{rrrclcl}
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & (-1)^2+y^2 & = & 4 & \quad & \left( \text{substitution} \right) \\
\scriptscriptstyle\mathrm{Arithmetic} & \implies & 1 + y^2 & = & 4 & \quad & \left( \text{applying the power} \right) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & y^2 & = & 3 & \quad & \left( \text{subtract }1\text{ from both sides} \right) \\
\scriptscriptstyle\xcancel{\mathrm{Arithmetic}} \to \mathrm{Algebra} & \implies & y & = & \pm\sqrt{3} & \quad & \left( \text{Extraction of Roots} \right) \\
\end{array}\nonumber \]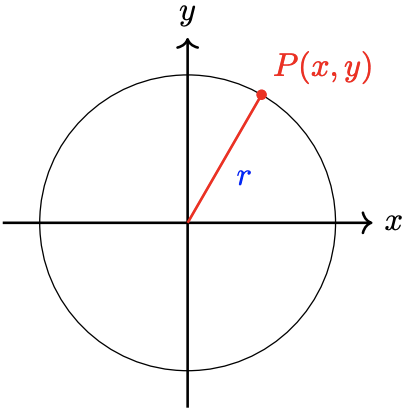

The points are \((-1,\sqrt{3})\) and \((-1,\sqrt{3})\), as shown at right. Note that \(\sqrt{3} \approx 1.732\).

Checkpoint \( \PageIndex{ 6 } \)

Find the coordinates of two points on the circle \(x^2 + y^2 = 1\) with \(y\)-coordinate \(\dfrac{1}{2}\).

Answer

\(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right),\left(-\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\)

The circle in Checkpoint \( \PageIndex{ 6} \) holds a special place in Trigonometry.

Definition: Unit Circle

The circle centered at the origin and having radius 1, is called the unit circle.

While the definition of the unit circle is only mentioned in passing here, it will become one of the foundational pieces of Trigonometry. We will revisit this later.

Later in this course, we will need to work with circles that do not have centers at the origin.

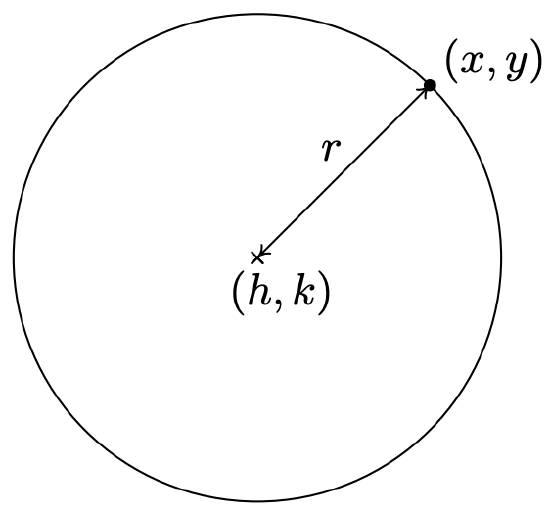
Figure \( \PageIndex{ 6 } \): A circle of radius \( r \) centered at the point \( \left( h,k \right) \)

Since Figure \( \PageIndex{ 6 } \) is a circle of radius \( r \), the point \((x,y)\) is on the circle if and only if its distance to \((h,k)\) is \(r\). By the Distance Formula, this means\[r = \sqrt{(x - h)^2 + (y-k)^2}\nonumber\]By squaring both sides of this equation, we get the standard equation of a circle.

Theorem: Standard Equation of a Circle

The standard equation of a circle with center \((h,k)\) and radius \(r \gt 0\) is \[(x-h)^2 + (y-k)^2 = r^2.\nonumber \]

Example \( \PageIndex{7} \)

Write the standard equation of the circle with center \((-2,3)\) and radius \(5\).

Solution

Here, \((h,k) = (-2,3)\) and \(r = 5\), so we get\[\begin{array}{rrcl}
& (x-(-2))^2+(y-3)^2 & = & (5)^2 \\
\implies & (x+2)^2+(y-3)^2 & = & 25 \\
\end{array}\nonumber\]

Checkpoint \( \PageIndex{7} \)

Graph \((x+2)^2+(y-1)^2 = 4\). Find the center and radius.

Answer

From the standard form of a circle we have that \(x + 2\) is \(x-h\), so \(h = -2\) and \(y - 1\) is \(y - k\) so \(k = 1\). This tells us that our center is \((-2,1)\). Furthermore, \(r^2 = 4\), so \(r = 2\). Thus we have a circle centered at \((-2,1)\) with a radius of \(2\). Graphing gives us

Angles in the Cartesian Coordinate System

Now that we have reacquainted ourselves with angles, circles, and the Cartesian coordinate system, the next natural evolution toward Trigonometry is introducing angles to the Cartesian coordinate plane.

Quadrants

Before we begin, it will be instrumental in this course to divide the Cartesian coordinate system into four sections, called quadrants, as seen in Figure \( \PageIndex{ 7 } \) below.

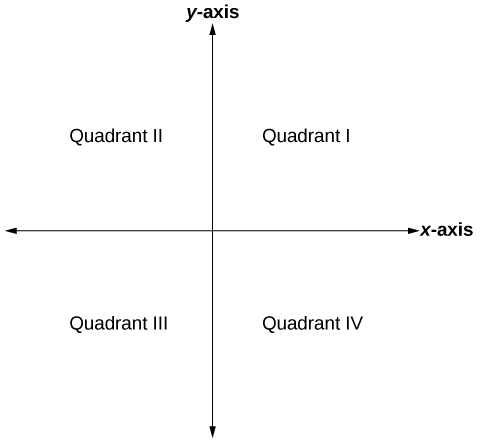
Figure \( \PageIndex{ 7 } \): The four quadrants of the Cartesian coordinate system

In quadrant I (QI), all values of \( x \) and \( y \) are positive. In quadrant II (QII), the \( y \)-values are positive, and the \( x \)-values are negative. In quadrant III (QIII), all values of \( x \) and \( y \) are negative. Finally, in quadrant IV (QIV), the \( x \)-values are positive, and the \( y \)-values are negative. Understanding these facts will be critical as we move forward.

Angles in Standard Position

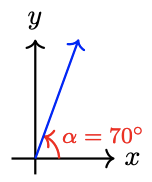
In general, and without worrying about a coordinate system, the degree measure of an angle depends only on the fraction of a whole rotation between its sides, not on the angle's location or position. To compare and analyze angles, we place them in standard position.

Definition: Standard Position of an Angle

An angle, \(\theta\), is said to be in standard position if

1. the vertex of the angle is at the origin and
2. the initial side of the angle is on the positive \( x \)-axis

Figure \( \PageIndex{ 8 } \) below shows several angles moved into standard position.

Figure \( \PageIndex{ 8 } \): Angles in nonstandard position (top row) and their equivalent angles in standard position (bottom row)

The \( 320^{ \circ } \) in Figure \( \PageIndex{ 8 } \) has its terminal side in quadrant IV. We denote this as \( 320^{ \circ } \in \mathrm{QIV}\). Likewise, the remaining angles in Figure \( \PageIndex{ 8 } \) are listed as \( 240^{ \circ } \in \mathrm{QIII} \), \( 130^{ \circ } \in \mathrm{QII} \), and \( 55^{ \circ } \in \mathrm{QI} \).

Example \( \PageIndex{ 8 } \)

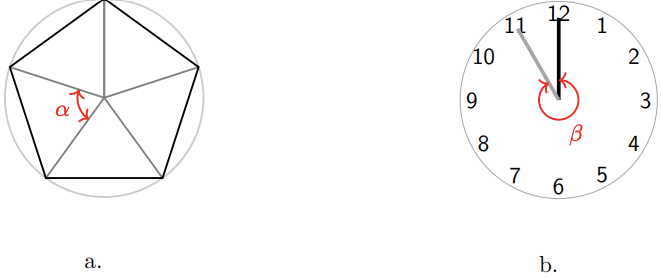
Find the degree measure of each angle shown below, state the quadrant where the angle terminates, and sketch the angle in standard position.

Solutions

1. The angle \(\alpha\) is one-fifth of a complete revolution, or\[\dfrac{1}{5}(360^{\circ}) = 72^{\circ}.\nonumber \]In standard position, \( \alpha = 72^{ \circ } \in \mathrm{QI} \), as shown in figure (a) below.

   

2. The angle \(\beta\) is \(\dfrac{11}{12}\) of a complete revolution, or\[\dfrac{11}{12}(360^{\circ}) = 330^{\circ}.\nonumber \]In standard position, \( \beta = 330^{ \circ } \in \mathrm{QIV} \). (See Figure (b).)

Checkpoint \( \PageIndex{ 8 } \)

Find the degree measure of each angle below, sketch the angle in standard position, and state the quadrant in which the angle terminates.

Answers

1. \(\theta = 120^{\circ} \in \mathrm{QII}\)

   

2. \(\alpha = 250^{ \circ } - 180^{ \circ } = 70^{\circ} \in \mathrm{QI}\)

   

Quadrantal Angles

If the terminal side of an angle in standard position lies on an axis, we call the angle a quadrantal angle. For example, \( 270^{ \circ } \) has a terminal side on the negative \( y \)-axis. Therefore, we would call \( 270^{ \circ } \) a quadrantal angle. Figure \( \PageIndex{ 9 } \) illustrates a few quadrantal angles; however, as we will learn shortly, there are infinite quadrantal angles.

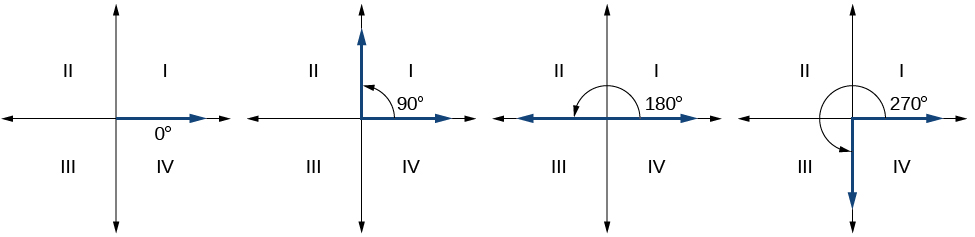
Figure \( \PageIndex{ 9 } \): Some quadrantal angles

Negative Angles

Aligning with what we said in Section 1.1, we say the angle is positive if an angle opens counterclockwise. If an angle opens clockwise, the angle is considered negative. For example, Figure \( \PageIndex{ 10 } \) shows the angle \( \alpha = -135^{ \circ } \), which terminates in \( \mathrm{QIII} \).

Figure \( \PageIndex{ 10 } \): A negative angle

Graphing positive and negative angles in standard position will be a critical skill in Trigonometry.

Coterminal Angles

Because \(360^{\circ}\) represents one complete revolution, we can add or subtract a multiple of \(360^{\circ}\) to any angle and the terminal side of the resulting angle will arrive at the same position. For example, the angles \(70^{\circ}\) and \(430^{\circ}\) have the same terminal side because \(430^{\circ}=70^{\circ}+360^{\circ}\). Such angles are called coterminal.

The angle \(790^{\circ}\) is also coterminal with \(70^{\circ}\), because \(790^{\circ}=70^{\circ}+2\left(360^{\circ}\right)\) (see Figure \( \PageIndex{ 11 } \) below).

Figure \( \PageIndex{ 11 } \): Graphical representations of coterminal angles

Coterminal angles need not be positive. For example, we could have been given \( \alpha = 140^{ \circ } \) and chosen to subtract \( 360^{ \circ } \) to get the coterminal angle \( -220^{ \circ } \) as shown in Figure \( \PageIndex{ 12 } \).

Figure \( \PageIndex{ 12 } \)

In fact, we could denote all angles coterminal to \( \alpha = 140^{ \circ } \) using the notation\[ 140^{ \circ } + 360^{ \circ }k, \text{ where } k \in \mathbb{Z}. \nonumber \]The symbol, \( \mathbb{Z} \), denotes the set of all integers (the set of numbers \( \ldots, -3, -2, -1, 0, 1, 2, 3, \ldots \)). This notation gets used frequently in mathematics from this point forward, so it is best to get used to it quickly.

Previously, we mentioned that the angles illustrated in Figure \( \PageIndex{ 9 } \) were only a "few quadrantal angles," implying there were more than what we listed. This was because, for example, given the quadrantal angle \( 90^{ \circ } \), we could generate an infinite number of other quadrantal angles with the same terminal side by considering\[ 90^{ \circ } + 360^{ \circ }k, \text{ where } k \in \mathbb{Z}. \nonumber \]Moreover, since the quadrantal angles only differ from each other by \( 90^{ \circ } \), we could generate all quadrantal angles with the single statement\[ 0^{ \circ } + 90^{ \circ }k, \text{ where } k \in \mathbb{Z}. \nonumber \]There is no need for the \( 0^{ \circ } \) angle in that formula, so we could shorten it up to just\[ 90^{ \circ }k, \text{ where } k \in \mathbb{Z}. \nonumber \]

Example \( \PageIndex{9} \)

Graph each of the angles below in standard position and classify them according to where their terminal side lies. Find three coterminal angles, at least one of which is positive and one of which is negative.

1. \(\alpha = 60^{\circ}\)
2. \(\beta = -225^{\circ}\)
3. \(\gamma = 540^{\circ}\)
4. \(\phi = -750^{\circ}\)

Solutions

1. To graph \(\alpha = 60^{\circ}\), we draw an angle with its initial side on the positive \(x\)-axis and rotate counter-clockwise \(\frac{60^{\circ}}{360^{\circ}} = \frac{1}{6}\) of a revolution. We see that \(\alpha\) is a Quadrant I angle. To find coterminal angles, we look for angles \(\theta\) of the form \(\theta = \alpha + 360^{\circ} \cdot k\), for some integer \(k\). When \(k = 1\), we get \(\theta = 60^{\circ} + 360^{\circ} = 420^{\circ}\). Substituting \(k = -1\) gives \(\theta = 60^{\circ} - 360^{\circ} = -300^{\circ}\). Finally, if we let \(k = 2\), we get \(\theta = 60^{\circ} + 720^{\circ} = 780^{\circ}\).
2. Since \(\beta = - 225^{\circ}\) is negative, we start at the positive \(x\)-axis and rotate clockwise \(\frac{225^{\circ}}{360^{\circ}} = \frac{5}{8}\) of a revolution. We see that \(\beta\) is a Quadrant II angle. To find coterminal angles, we proceed as before and compute \(\theta = -225^{\circ} + 360^{\circ} \cdot k\) for integer values of \(k\). We find \(135^{\circ}\), \(-585^{\circ}\) and \(495^{\circ}\) are all coterminal with \(-225^{\circ}\).

   

3. Since \(\gamma = 540^{\circ}\) is positive, we rotate counter-clockwise from the positive \(x\)-axis. One full revolution accounts for \(360^{\circ}\), with \(180^{\circ}\), or \(\frac{1}{2}\) of a revolution remaining. Since the terminal side of \(\gamma\) lies on the negative \(x\)-axis, \(\gamma\) is a quadrantal angle. All angles coterminal with \(\gamma\) are of the form \(\theta = 540^{\circ} + 360^{\circ} \cdot k\), where \(k\) is an integer. Working through the arithmetic, we find three such angles: \(180^{\circ}\), \(-180^{\circ}\) and \(900^{\circ}\).
4. The Greek letter \(\phi\) is pronounced "fee" or "fie," and since \(\phi\) is negative, we begin our rotation clockwise from the positive \(x\)-axis. Two full revolutions account for \(720^{\circ}\), with just \(30^{\circ}\) or \(\frac{1}{12}\) of a revolution to go. We find that \(\phi\) is a Quadrant IV angle. To find coterminal angles, we compute \(\theta = -750^{\circ} + 360^{\circ} \cdot k\) for a few integers \(k\) and obtain \(-390^{\circ}\), \(-30^{\circ}\) and \(330^{\circ}\).

   

Checkpoint \( \PageIndex{ 9 } \)

Find two angles coterminal with \(102^{\circ}\), one positive and one negative.

Answer

\(462^{\circ},-258^{\circ}\)

---

Skills Refresher

Review the following skills you will need for this section.

Skills Refresher

In Problems 1 - 5, find the slope and \( y \)-intercept of the graph for the given equation (do not graph).

1. \( y = 5.2x - 1.9 \)

2. \( y = x \)

3. \( y = -8 \)

4. \( x = 7 \)

5. \( 12y - 10x = 5 \)

In Problems 6 and 7, write the equation of the line that satisfies the given conditions.

6. The line goes through the points \( \left( -2,6 \right) \) and \( \left( 3,-4 \right) \).

7. The line goes through the points \( \left( 5,-7 \right) \) and \( \left( 5,-5 \right) \).

In Problems 8 - 15, determine if the statement is true or false.

8. \(\sqrt{a^2+b^2}=a+b\)

9. \(\sqrt{36+64}=6+8\)

10. \(\sqrt{16 x^4}=4 x^2\)

11. \(\sqrt{2 x} \sqrt{3 y}=\sqrt{6 x y}\)

12. \(\sqrt{5 x}+\sqrt{3 x}=\sqrt{8 x}\)

13. \(\sqrt{4+N}=2+\sqrt{N}\)

14. \(\sqrt{\dfrac{x}{4}}=\dfrac{\sqrt{x}}{2}\)

15. \(\sqrt{\dfrac{3}{2}}=\dfrac{\sqrt{6}}{2}\)

In Problems 16 - 19, solve the equation. If no solution exists, state why.

16. \(x^2 - 81 = 0\)

17. \(2 y^2 - 98 = 0\)

18. \(x^2 + 12 = 8\)

19. \(-3x^2 + 19 = 10\)

Answers

1. \( m = 5.2 \quad \left( 0,-1.9 \right)\)

2. \( m = 1 \quad \left( 0,0 \right) \)

3. \( m = 0 \quad \left( 0,-8 \right) \)

4. The slope is undefined and there is not a \( y \)-intercept.

5. \( m = \frac{5}{6} \quad \left( 0,\frac{5}{12} \right) \)

6. \( y = -2x + 2 \)

7. \( x = 5 \)

8. False

9. False

10. True

11. True

12. False

13. False

14. True

15. True

16. \( x = \pm 9 \)

17. \( y = \pm 7 \)

18. No solution because \( x^2 \) should never be negative, but when solving, we get \( x^2 = -4 \).

19. \( x = \pm \sqrt{3} \)

---

Homework

Vocabulary Check

1. The ___ of a line is also known as the "steepness" of the line.

2. A(n) ___ slope for a line results in a vertical line.

3. When computing\[ \dfrac{\Delta y}{\Delta x}, \nonumber \]you are computing the ___ of a line.

4. An alternative to saying "slope" of a line is to say the ___ of ___ of the line.

5. The two common forms of the equation of a line are the ___ form and the ___ form.

Concept Check

6. A line is said to be increasing on an interval if its slope is ___ on that interval.

7. A line is said to be constant on an interval if its slope is ___ on that interval.

8. Explain why the Distance Formula,\[d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2},\nonumber \]cannot be simplified to\[(x_2-x_1)+(y_2-y_1).\nonumber \]

9. What is a unit circle, and what is its equation?

10. In which quadrant are the \( x \)-values for points negative but the \( y \)-values are positive?

11. Explain what it means for angles to be coterminal. Demonstrate by creating three coterminal angles, one of which is a negative angle.

True or False? For Problems 12 - 17, determine if the statement is true or false. If true, cite the definition or theorem stated in the text supporting your claim. If false, explain why it is false and, if possible, correct the statement.

12. A vertical line has a slope equal to \( 0 \).

13. Only straight lines have slopes - all other lines do not.

14. If the \( x \)- or \( y \)-value of a point is \( 0 \), the point must lie on an axis.

15. In the notation\[ \dfrac{\Delta y}{\Delta x}, \nonumber \]\( \Delta \) stands for "triangle."

16. The first value for which you evaluate a function is called the initial value of the function.

17. Positive angles open clockwise.

Basic Skills

In Exercises 18 - 27, find the slope-intercept form of the line that passes through the given points.

18. \(\ P(0, 0), \quad Q(−3, 5)\)

19. \(\ P(−1, −2), \quad Q(3, −2)\)

20. \(\ P(5, 0), \quad Q(0, −8)\)

21. \(\ P(3, −5), \quad Q(7, 4)\)

22. \(\ P(−1, 5), \quad Q(7, 5)\)

23. \(\ P(4, −8), \quad Q(5, −8)\)

24. \(\ P\left(\frac{1}{2}, \frac{3}{4}\right), \quad Q\left(\frac{5}{2},-\frac{7}{4}\right)\)

25. \(\ P\left(\frac{2}{3}, \frac{7}{2}\right), \quad Q\left(-\frac{1}{3}, \frac{3}{2}\right)\)

26. \(\ P(\sqrt{2},-\sqrt{2}), \quad Q(-\sqrt{2}, \sqrt{2})\)

27. \(\ P(-\sqrt{3},-1), \quad Q(\sqrt{3}, 1)\)

In Exercises 28 - 37, find both the point-slope form and the slope-intercept form of the line with the given slope which passes through the given point.

28. \(\ m = 3, \quad P(3, −1)\)

29. \(\ m = −2, \quad P(−5, 8)\)

30. \(\ m = −1, \quad P(−7, −1)\)

31. \(\ m=\frac{2}{3}, \quad P(-2,1)\)

32. \(\ m=-\frac{1}{5}, \quad P(10,4)\)

33. \(\ m=\frac{1}{7}, \quad P(-1,4)\)

34. \(\ m = 0, \quad P(3, 117)\)

35. \(\ m=-\sqrt{2}, \quad P(0,-3)\)

36. \(\ m=-5, \quad P(\sqrt{3}, 2 \sqrt{3})\)

37. \(\ m = 678, \quad P(−1, −12)\)

In Exercises 38 - 43, graph the line. Find the slope, \(y\)-intercept and \(x\)-intercept, if any exist.

38. \(\ y=2 x-1\)

39. \(\ y=3-x\)

40. \(\ y=3\)

41. \(\ y=0\)

42. \(\ y=\frac{2}{3} x+\frac{1}{3}\)

43. \(\ y=\frac{1-x}{2}\)

Parallel Lines. Recall from Intermediate Algebra that parallel lines have the same slope. (Please note that two vertical lines are also parallel despite having an undefined slope.) In Problems 44 - 49, you are given a line and a point that is not on that line. Find the line parallel to the given line which passes through the given point.

44. \(\ y = 3x + 2, P(0, 0) \)

45. \(\ y = −6x + 5, P(3, 2)\)

46. \(\ y=\frac{2}{3} x-7, P(6,0)\)

47. \(\ y=\frac{4-x}{3}, P(1,-1)\)

48. \(\ y = 6, P(3, −2)\)

49. \(\ x = 1, P(−5, 0)\)

Perpendicular Lines. Recall from Intermediate Algebra that two non-vertical lines are perpendicular if and only if they have negative reciprocal slopes. That is to say, if one line has slope \(\ m_{1}\) and the other has slope \(\ m_{2}\) then \(\ m_{1} \cdot m_{2}=-1\). Please note that a horizontal line is perpendicular to a vertical line and vice versa, so we assume \(\ m_{1} \neq 0\) and \(\ m_{2} \neq 0\). In Problems 50 - 55, you are given a line and a point not on that line. Find the line perpendicular to the given line which passes through the given point.

50. \(\ y=\frac{1}{3} x+2, P(0,0)\)

51. \(\ y=-6 x+5, P(3,2)\)

52. \(\ y=\frac{2}{3} x-7, P(6,0)\)

53. \(\ y=\frac{4-x}{3}, P(1,-1)\)

54. \(\ y = 6, P(3, −2)\)

55. \(\ x = 1, P(−5, 0)\)

For Problems 56 - 58, find the distance between the points. Give your answer as an exact value, then as a decimal rounded to hundredths.

56.  

    

57.  

    

58.  

    

For Problems 59 - 64, find the distance between the points.

59. (1, 1), (4, 5)

60. (−1, 1), (5, 9)

61. (2, −3), (−2, −1)

62. (5, −4), (−1, 1)

63. (3, 5), (−2, 5)

64. (−2, −5), (−2, 3)

65.  

    1. Write an expression for the distance between the points (\(x, y\)) and \((−3, 4)\).

    2. Write an equation that says "The distance between the points (\(x, y\)) and \((−3, 4)\) is \(5\) units."

66.  

    1. Write an expression for the distance between the points \((−6, −1)\) and (\(h, k\)).

    2. Write an equation that says, "The point \((−6, −1)\) is \(3\) units from the point (\(h, k\))."

67.  

    1. Complete the table of values for the equation \(x^2+y^2 = 25\).

       \(x\)	-5	-4	-3	-2	-1	0	1	2	3	4	5
       \(y\)

    2. Plot the points and graph the equation.

       

68.  

    1. Complete the table of values for the equation \(x^2+y^2 = 1\).

       \(x\)	-1	-0.8	-0.6	0	0.6	0.8	2
       \(y\)

    2. Plot the points and graph the equation.

       

69.  

    1. Sketch a graph of all points in the plane that lie 6 units from the origin.

    2. Write an equation for your graph.

70.  

    1. Sketch a graph of all points in the plane that lie \(\sqrt{12}\) units from the origin.

    2. Write an equation for your graph.

71.  

    1. Sketch a graph of all points in the plane that lie less than 3 units from the origin.

    2. Write an inequality for your graph.

72.  

    1. Sketch a graph of all points in the plane that lie more than 5 units from the origin.

    2. Write an inequality for your graph.

73.  

    1. Explain why the solutions of the equation \(x^2+y^2=16\) must have \(-4 \leq x \leq 4\).

    2. What does part (a) tell you about the graph of the equation?

74.  

    1. Explain why the solutions of the equation \(x^2+y^2=100\) must have \(-10 \leq x \leq 10\)

    2. What does part (a) tell you about the graph of the equation?

75. The point \((1,-3)\) lies on a circle centered at the origin. What is the radius of the circle?

76. The point \((-2, \sqrt{6})\) lies on a circle centered at the origin. What is the radius of the circle?

77. Find the coordinates of the points on the unit circle.

    

78.  

    1. Use the Distance Formula to write an equation for the circle of radius 6 centered at the point \((3, −2)\).

    2. Use the Distance Formula to derive an equation for the circle of radius \(r\) centered at the point \((h, k)\).

For Problems 79 and 80, find the coordinates of the indicated points on each circle.

79. \((x-4)^2 + (y-5)^2 = 9\)

    

80. \((x+3)^2 + (y-1)^2 = 25\)

    

81. How many degrees are in each angle?

    1. \(\frac{3}{5}\) of one rotation

    2. \(\frac{3}{10}\) of one rotation

    3. \(\frac{4}{3}\) of one rotation

    4. \(\frac{8}{3}\) of one rotation

82. How many degrees are in each angle?

    1. \(\frac{5}{6}\) of one rotation

    2. \(\frac{3}{8}\) of one rotation

    3. \(\frac{7}{4}\) of one rotation

    4. \(\frac{7}{12}\) of one rotation

83. What fraction of a complete rotation is represented by each angle?

    1. \(45^{\circ}\)

    2. \(300^{\circ}\)

    3. \(540^{\circ}\)

    4. \(420^{\circ}\)

84. What fraction of a complete rotation is represented by each angle?

    1. \(60^{\circ}\)

    2. \(240^{\circ}\)

    3. \(450^{\circ}\)

    4. \(150^{\circ}\)

For Problems 85 - 90, find two angles, one positive and one negative, that are coterminal with the given angle.

85. \(40^{\circ}\)

86. \(160^{\circ}\)

87. \(215^{\circ}\)

88. \(250^{\circ}\)

89. \(305^{\circ}\)

90. \(340^{\circ}\)

For Problems 91 - 96, find a positive angle between \(0^{\circ}\) and \(360^{\circ}\) that is coterminal with the given angle.

91. \(-65^{\circ}\)

92. \(-140^{\circ}\)

93. \(-290^{\circ}\)

94. \(-325^{\circ}\)

95. \(-405^{\circ}\)

96. \(-750^{\circ}\)

Synthesis Questions

97. Show that the triangle with vertices \((0, 0)\), \((6, 0)\), and \((3, 3)\) is an isosceles right triangle, that is, a right triangle with two sides of the same length.

98. Two opposite vertices of a square are \(A(−9, −5)\) and \(C(3, 3)\).

    1. Find the length of a diagonal of the square.

    2. Find the length of the side of the square.

99. Find all of the points on the line \(\ y = 2x + 1\) which are \(4\) units from the point \((-1, 3)\).

100. Sketch a triangle with vertices \((10, 1)\), \((3, 1)\), and \((5, 9)\), and find its perimeter. Round your answer to tenths.

101. Sketch a triangle with vertices \((−1, 5)\), \((8, −7)\), and \((4, 1)\), and find its perimeter. Round your answer to tenths.

For Problems 102 and 103, interpret the equations as statements about distance.

102. \(\sqrt{(x-4)^2+(y+1)^2}=3\)

103. \(\sqrt{(-2-h)^2+(5-k)^2}=l\)

For Problems 104 - 107,
(a) graph the equation and
(b) find the circumference of the circle.

104. \(x^2+y^2 = 36\)

     

105. \(x^2+y^2=16\)

     

106. \(4 x^2+4 y^2=16\)

     

107. \(2 x^2+2 y^2=18\)

     

108. Give the coordinates of two points on the circle in Problem 103 that have \(y = −4\). Plot those points on your graph.

109. Give the coordinates of two points on the circle in Problem 103 that have \(x = −2\). Plot those points on your graph.

Applications

110. Distance. Matt can walk comfortably at 3 miles per hour. Find a linear equation representing the total distance Matt can walk in \(\ t\) hours, assuming he takes no breaks.

111. Distance. Paige is sailing and is currently 3 miles west and 5 miles south of the harbor. She heads directly towards an island 8 miles west and 7 miles north of the harbor. How far is Paige from the island?

112. Distance. Nam is 100 meters east and 250 meters north of Kristen. He walks directly towards a tree 220 meters east and 90 meters north of Kristen. How far is Nam from the tree?

113. Work. Mike can stuff six envelopes per minute. Find a linear model representing the total number of envelopes Mike can stuff after \(t\) hours, assuming he doesn’t take any breaks.

114. Cost. A landscaping company charges $45 per cubic yard of mulch plus a delivery charge of $20. Find a linear model that computes the total cost \(\ C\) (in dollars) to deliver \(\ x\) cubic yards of mulch.

115. Charges. A plumber charges $50 for a service call plus $80 per hour. If she spends no longer than 8 hours a day at any one site, find a linear model that represents her total daily charges \(\ C\) (in dollars) as a function of time \(\ t\) (in hours) spent at any one given location.

116. Salary. A salesperson is paid $200 per week plus 5% commission on her weekly sales of \(\ x\) dollars. Find a linear model that represents her total weekly pay, \(\ W\) (in dollars) in terms of \(\ x\). What must her weekly sales be to earn $475.00 for the week?

117. Cost. An on-demand publisher charges $22.50 to print a 600-page book and $15.50 to print a 400-page book. Find a linear model that models the cost of a book \(\ C\) as a function of the number of pages \(\ p\). Interpret the slope of the linear model and find and interpret what happens if \(\ p = 0\).

118. Cost. The Topology Taxi Company charges $2.50 for the first fifth of a mile and $0.45 for each additional fifth of a mile. Find a linear model that models the taxi fare \(\ F\) as a function of the number of miles driven, \(\ m\). Interpret the slope of the linear model and find and interpret what happens if \(\ m = 0\).

119. Physics. Water freezes at \(\ 0^{\circ}\) Celsius and \(\ 32^{\circ}\) Fahrenheit and it boils at \(\ 100^{\circ} \mathrm{C}\) and \(\ 212^{\circ} \mathrm{F}\).

     1. Find a linear model \(\ F\) that expresses temperature in the Fahrenheit scale in terms of degrees Celsius. Use this model to convert \(\ 20^{\circ} \mathrm{C}\) into Fahrenheit.

     2. Find a linear model \(\ C\) that expresses temperature in the Celsius scale in terms of degrees Fahrenheit. Use this model to convert \(\ 110^{\circ} \mathrm{F}\) into Celsius.

120. Howling Sasquatch. Legend has it that a bull Sasquatch in rut will howl approximately 9 times per hour when it is \(\ 40^{\circ} \mathrm{F}\) outside and only 5 times per hour if it’s \(\ 70^{\circ} \mathrm{F}\). Assuming that the number of howls per hour, \(\ N\), can be represented by a linear model in terms of temperature Fahrenheit, find the number of howls per hour he’ll make when it’s only \(\ 20^{\circ} \mathrm{F}\) outside.

121. Computing Angles.

     1. Through what angle does the hour hand of a clock rotate between 2 pm and 10 pm?

     2. Through what angle does the hour hand of a clock rotate between 2 am and 10 pm?

122. Computing Angles.

     1. Through what angle does the hour hand of a clock rotate between 3:25 am and 3:50 am?

     2. Through what angle does the hour hand of a clock rotate between 4:10 pm and 6:25 pm?

123. Astronomy. The Distance Formula can be modified to compute distances between objects in three-dimensional space. To do so, we must expand the Cartesian coordinate system to include one more spatial dimension. In three-space, coordinates are listed in ordered triples, such as \( (x,y,z) \). If we have two points, \( P(x_1,y_1,z_1) \) and \( Q(x_2,y_2,z_2) \), in three-dimensional space, the distance between these points is\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}. \nonumber \]Suppose our Sun is given the very special coordinate of \( (0,0,0) \) (thereby affirming that we are the center of the universe). Compute the distance between each star (these computed distances are in light-years). Round answers to the nearest hundredth of a light-year.

     1. Our Sun, \( (0,0,0) \), and Alpha Centauri, \( (-1.8,0, 3.9) \).

     2. Our Sun, \( (0,0,0) \), and Sirius, \( (-3.4, -3.1, 7.3) \).

     3. Our Sun, \( (0,0,0) \), and Polaris, \( (99.6, 28.2, 376.0) \).

     4. Alpha Centauri, \( (-1.8,0,3.9) \), and Sirius, \( (-3.4, -3.1, 7.3) \).

     5. Zubenelgenubi, \( (64.6,-22.0,23.0) \), and Polaris, \( (99.6, 28.2, 376.0) \).

Computing Angles. For Problems 124 - 129, calculate the degree measure of the unknown angle and sketch the angle in standard position.

124.  

     

125.  

     

126.  

     

127.  

     

128.  

     

129.  

     

Challenge Problems

130. In this problem, we’ll show that any angle inscribed in a semi-circle must be a right angle. The figure shows a triangle inscribed in a unit circle, one side lying on the diameter of the circle and the opposite vertex at point \((p, q)\) on the circle.

     

     1. What are the coordinates of the other two vertices of the triangle? What is the length of the side joining those vertices?

     2. Use the Distance Formula to compute the lengths of the other two sides of the triangle.

     3. Show that the sides of the triangle satisfy the Pythagorean Theorem, \(a^2 + b^2 = c^2\).

131. We shall now prove that \(\ y=m_{1} x+b_{1}\) is perpendicular to \(\ y=m_{2} x+b_{2}\) if and only if \(\ m_{1} \cdot m_{2}=-1\). To make our lives easier we shall assume that \(\ m_{1}>0\) and \(\ m_{2}<0\). We can also "move" the lines so that their point of intersection is the origin without messing things up, so we’ll assume \(\ b_{1}=b_{2}=0\). (Take a moment with your classmates to discuss why this is okay.) Graphing the lines and plotting the points \(\ O(0, 0)\), \(\ P\left(1, m_{1}\right)\) and \(\ Q\left(1, m_{2}\right)\) gives us the following set up.

     

     The line \(\ y=m_{1} x\) will be perpendicular to the line \(\ y=m_{2} x\) if and only if \(\ \triangle O P Q\) is a right triangle. Let \(\ d_{1}\) be the distance from \(\ O\) to \(\ P\), let \(\ d_{2}\) be the distance from \(\ O\) to \(\ Q\) and let \(\ d_{3}\) be the distance from \(\ P\) to \(\ Q\). Use the Pythagorean Theorem to show that \(\ \triangle O P Q\) is a right triangle if and only if \(\ m_{1} \cdot m_{2}=-1\) by showing \(\ d_{1}^{2}+d_{2}^{2}=d_{3}^{2}\) if and only if \(\ m_{1} \cdot m_{2}=-1\).