1.1: Angles and Basic Geometry

Suggested Prerequisite Topics

This section is designed assuming you understand the following topics from Arithmetic and Algebra.

• Order of Operations
• Number systems (specifically, the irrational numbers)
• Proper calculator usage
• Variables and algebraic expressions
• Solving linear equations

Learning Objectives

• Identify acute, obtuse, right, and straight angles.
• Compute the complement and supplement of an angle.
• Determine the number of degrees in a partial rotation.
• Use vertical, alternate interior, or corresponding angles to solve for an angle.
• Find the circumference and area of a circle.

Angles

A ray is a line segment in which one of the two endpoints is pushed off infinitely distant from the other (see Figure \( \PageIndex{ 1 } \)). The point from which the ray originates is called the initial point of the ray. A ray can be described as a "half-line."

Figure \( \PageIndex{ 1 } \): A ray with initial point \( P \).

When two rays share a common initial point, they form an angle, and the shared initial point is called the angle's vertex. Figure \( \PageIndex{ 2 } \) shows two examples of what are commonly considered as angles.

Figure \( \PageIndex{ 2 } \): An angle with vertex \( P \) (left) and an angle with vertex \( Q \) (right)

However, Figure \( \PageIndex{ 3 } \) also depicts angles - albeit these are, in some sense, extreme cases. In the first case, the two rays are directly opposite each other, forming what is known as a straight angle; in the second, the rays are identical, so the "angle" is indistinguishable from the ray itself.

Figure \( \PageIndex{ 3 } \): A straight angle (left) and a "closed" angle (right)

The measure of an angle is a number that indicates the amount of rotation that separates the rays of the angle. There is one immediate problem with this, as should be evident from Figure \( \PageIndex{ 4 } \) below.

Figure \( \PageIndex{ 4 } \): The ambiguity of angles

Which amount of rotation are we attempting to quantify?

We have just discovered that this diagram describes at least two angles. Clearly, these two angles have different measures because one appears to represent a larger rotation than the other, so we must label them differently.

In Trigonometry, we often use lowercase Greek letters to represent the measure of the angle. For example, we use the Greek letters \(\alpha\) (alpha) and \(\beta\) (beta) as representations of the unknown angle measures in Figure \( \PageIndex{ 5 } \).

Figure \( \PageIndex{ 5 } \)

Identifying the lowercase Greek letters will be beneficial in this course. Table \( \PageIndex{ 1 } \) summarizes the (lowercase) Greek alphabet. The letters in bold are the ones most commonly used within Trigonometry.

Table \( \PageIndex{ 1 } \) Lowercase Letters in the Greek Alphabet

\begin{aligned}
&\quad \quad \quad \quad \quad \text { Greek Alphabet }\\
&\begin{array}{|cc|cc|cc|}
\hline \boldsymbol{\alpha} & \textbf { alpha } & \boldsymbol{\beta} & \textbf { beta } & \boldsymbol{\gamma} & \textbf { gamma } \\
\hline \delta & \text { delta } & \epsilon & \text { epsilon } & \zeta & \text { zeta } \\
\hline \eta & \text { eta } & \boldsymbol{\theta} & \textbf { theta } & \iota & \text { iota } \\
\hline \kappa & \text { kappa } & \lambda & \text { lambda } & \mu & \text { mu } \\
\hline \nu & \text { nu } & \xi & \text { xi } & o & \text { omicron } \\
\hline \pi & \text { pi } & \rho & \text { rho } & \sigma & \text { sigma } \\
\hline \boldsymbol{\tau} & \textbf { tau } & v & \text { upsilon } & \boldsymbol{\phi} & \textbf { phi } \\
\hline \chi & \text { chi } & \psi & \text { psi } & \boldsymbol{\omega} & \textbf { omega } \\
\hline
\end{array}
\end{aligned}

Note: \( \pi \) is a Universal Constant

The lowercase Greek letter \( \pi \) is never used as a symbolic representation of an unknown angle. \( \pi \) is reserved for the universal constant \( \pi \approx 3.141592654 \).¹

Another ambiguity that sneaks into angular measure is which direction the angle is "opening." We need to extend our notion of "angle" from merely measuring an extent of rotation to quantities associated with real numbers. To that end, we introduce the concept of an oriented angle. As its name suggests, in an oriented angle, the direction of the rotation is essential. We imagine the angle swept out starting from an initial side and ending at a terminal side, as shown below in Figure \( \PageIndex{ 6 } \). When the rotation is counterclockwise from the initial side to the terminal side, we say that the angle is positive; when the rotation is clockwise, we say that the angle is negative.

Figure \( \PageIndex{ 6 } \): A positive angle (left) and a negative angle (right)

Alternative Angle Notations

We have already mentioned that we will frequently use lowercase Greek letters when referencing angles; however, this is not the only convention that exists when referencing an angle. Angles may be labeled with a single letter at the vertex as long as it is clear that there is only one such angle. For example, in Figure \( \PageIndex{ 7 } \) (below), it is clear that angle \( A \) is the vertex. There is no ambiguity about this fact. Therefore, an acceptable notation to reference this angle is \( \angle A \) (some texts might use the notation \( m \angle A \), meaning "the measure of angle \( A \)").

Figure \( \PageIndex{ 7 } \)

However, if there is the possibility for confusion, angles are labeled by specifying 3 points, with the center point being the angle's vertex. Therefore, we could reference the angle in Figure \( \PageIndex{ 7 } \) as \( \angle BAC \). The first letter indicates the initial side of the angle, the middle is the vertex, and the last letter indicates the terminal side. It is crucial that the center letter in this notation is the angle's vertex.

Degree Measure

One commonly used system to measure angles is degree measure. Quantities measured in degrees are denoted by the familiar "\(^{\circ}\)" symbol. We define degree measure by dividing the full rotation around the circle into 360 segments. That is, we define \(1^{\circ}\) to represent the measure of an angle which constitutes \(\frac{1}{360}\) of a revolution.

Figure \( \PageIndex{ 8 } \) shows the degree measures for a full, half, and quarter revolution. Since we define a full revolution as being \( 360^{ \circ } \), half of a revolution measures \(\frac{1}{2} \left(360^{\circ}\right) = 180^{\circ}\), a quarter of a revolution (a right angle) measures \(\frac{1}{4} \left(360^{\circ}\right) = 90^{\circ}\), and so on.

Figure \( \PageIndex{ 8 } \): A full revolution (left), straight angle (middle), and right angle (right)

In Figure \( \PageIndex{ 8 } \), we have used the small square "\(\square\)" to denote a right angle, as is commonplace in Geometry.

Recall that if an angle measures strictly between \(0^{\circ}\) and \(90^{\circ}\), it is called an acute angle, and if it measures strictly between \(90^{\circ}\) and \(180^{\circ}\) it is called an obtuse angle. It is important to note that, theoretically, we can know the measure of any angle as long as we know the proportion it represents of the entire revolution. For instance, the measure of an angle which represents a rotation of \(\frac{2}{3}\) of a revolution would measure \(\frac{2}{3} \left(360^{\circ}\right) = 240^{\circ}\), the measure of an angle which constitutes only \(\frac{1}{12}\) of a revolution measures \(\frac{1}{12} \left(360^{\circ}\right) = 30^{\circ}\), and an angle which indicates no rotation at all is measured as \(0^{\circ}\) (see Figure \( \PageIndex{ 9 } \)).

Figure \( \PageIndex{ 9 } \): An obtuse angle (left), an acute angle (middle), and a "closed" angle (right)

Recall that two acute angles are called complementary angles if their measures add to \(90^{\circ}\). Two angles, either a pair of right angles or one acute angle and one obtuse angle, are called supplementary angles if their measures add to \(180^{\circ}\). In the diagram below, the angles \(\alpha\) and \(\beta\) are supplementary while the pair \(\gamma\) and \(\theta\) are complementary angles.

Figure \( \PageIndex{ 10 } \): Supplementary angles, \( \alpha \) and \( \beta \) (left) and complementary angles, \( \gamma \) and \( \theta \) (right)

Caution: We Define Complementary and Supplementary Angles to be Positive

In this text, we will restrict the definition of complementary and supplementary angles to positive angles only. That is, we will not say that \( \alpha = -20^{ \circ } \) and \( \beta = 110^{ \circ } \) are complementary despite their sum being \( 90^{ \circ } \). Other textbooks allow for this silliness, but the truth is that there is no need to expand these definitions to include negative angles.

Finally, in practice, the distinction between the angle itself and its measure is blurred so that the sentence "\(\alpha\) is an angle measuring \(42^{\circ}\)" is often abbreviated as "\(\alpha = 42^{\circ}\)."

Example \( \PageIndex{ 1 } \)

Consider the figure below.

1. Which angle pairs are supplementary?
2. Which angle pairs are complementary?
3. Which angles are obtuse?
4. Which angles are acute?

Solutions

1. \(\angle A O C\) and \(\angle B O C\) are supplementary, \( \angle A O D \) and \( \angle B O D \) are supplementary, and \( \angle A O E \) and \( \angle B O E \) are supplementary.
2. \(\angle D O E\) and \(\angle B O E\) are complementary.
3. \(\angle A O C\), \( \angle A O E \), and \( \angle D O C \) are each obtuse angles.
4. \(\angle B O C\), \( \angle B O E \), and \( \angle D O E \) are each acute angles.

It could be argued in Example \( \PageIndex{ 1d } \) that \( \angle C O E \) is acute; however, there is no valid reference for the measure of \( \angle C O B \) and \( \angle B O E \) - only a visual cue. Therefore, we avoid assuming that \( \angle C O E \) is acute.

Checkpoint \(\PageIndex{1}\)

1. State the complement of \( 27^{ \circ } \).
2. State the supplement of \( 27^{ \circ } \).
3. State the complement of \( \alpha \).
4. State the supplement of \( \theta \).

Answer

1. \( 63^{ \circ } \)
2. \( 153^{ \circ } \)
3. \( 90^{ \circ } - \alpha \)
4. \( 180^{ \circ } - \theta \)

The measuring "system" we use to measure angles is formally called the Decimal Degree (DD) system; however, you might know of an alternate form of this system called the Degree-Minute-Second (DMS) system. While we will eventually use this angular measurement system (specifically, in some applications), it is not necessary to introduce it at this time. Moreover, later in the course, we will introduce a "better" angular measurement system (known as radian measure) without which we could not perform Calculus. Again, there is no need to teach that system of angular measure at this time, but it's always a good idea to know that a change is on the horizon.

Angles in Rotations

Now that we have some basic information about angles and have reintroduced ourselves to a measurement system for angles, it's time to introduce an application of angular measure. Specifically, we will learn to use angles to describe rotation. For example, think of the minute hand on a clock. The minute hand moves through one complete rotation every hour, or \(360^{\circ}\). In two hours, the minute hand rotates through \(720^{\circ}\).

Example \( \PageIndex{ 2 } \)

Through how many degrees does the minute hand rotate in an hour and a half? In forty minutes?

Solution

Look at the figure above. An hour and a half represents 1.5 complete rotations, or\[1.5(360^{\circ}) = 540^{\circ}.\nonumber \]Forty minutes is two-thirds of an hour, so the minute hand rotates through\[\dfrac{2}{3} (360^{\circ}) = 240^{\circ}\nonumber \]

Checkpoint \( \PageIndex{ 2 } \)

The volume control on an amplifier is a dial with ten settings, as shown below. Through how many degrees would you rotate the dial to increase the volume level from 0 to 7?

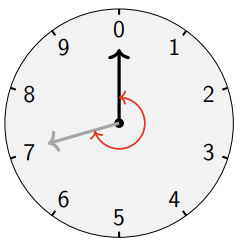
Answer

\(252^{\circ}\)

Geometry Necessary for Trigonometry

Trigonometry requires a decent grasp of basic Geometry. As such, let's review some pertinent topics. The topics relating to the geometry of triangles are reserved for Section 1.2.

Vertical Angles

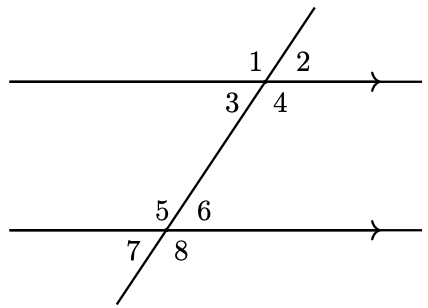
Non-adjacent angles formed by the intersection of two straight lines are called vertical angles. For example, \(\angle 1\) and \(\angle 3\) in Figure \( \PageIndex{ 11 } \) are vertical angles, as are the angles labeled \(\angle 2\) and \(\angle 4\).

Figure \( \PageIndex{ 11 } \)

Two angles are defined to be equal if their measures are equal. Having clarified this, we introduce a theorem that is very useful for deriving other concepts from Geometry.

Theorem: Vertical Angles

Vertical angles are equal (also known in Geometry as congruent).

Proof

Suppose two lines intersect, as shown in Figure \( \PageIndex{ 11 } \). Since \( \angle 1 + \angle 2 \) forms a straight angle,\[ \angle 1 + \angle 2 = 180^{\circ}.\nonumber \]By a similar argument,\[ \angle 1 + \angle 4 = 180^{\circ}.\nonumber \]Therefore,\[ \angle 1 + \angle 2 = 180^{\circ} = \angle 1 + \angle 4.\nonumber \]That is,\[ \angle 2 = \angle 4.\nonumber \]By a similar set of arguments, we can show that \[ \angle 1 = \angle 3.\nonumber \]Hence, it must always be the case that vertical angles are congruent.

Alternate Interior Angles

A line intersecting two parallel lines forms eight angles, as shown in Figure \( \PageIndex{ 12 } \). This line is called a transversal. There are four pairs of vertical angles and four pairs of corresponding angles, or angles in the same position relative to the transversal on each parallel line.

Figure \( \PageIndex{ 12 } \): Two parallel lines "cut" by a transversal.

\( \angle 1 \) and \( \angle 5 \) are corresponding angles, as are \( \angle 4 \) and \( \angle 8 \). Finally, \( \angle 3 \) and \( \angle 6 \) are called alternate interior angles, as are \( \angle 4 \) and \( \angle 5 \).

Theorem: Alternate Interior Angles

If a transversal intersects parallel lines, the alternate interior angles are equal.

Proof

Suppose a transversal cuts two parallel lines. Label the angles as in Figure \( \PageIndex{ 2 } \). We know that the corresponding and vertical angles are congruent if a transversal intersects two parallel lines. Therefore,\[ \angle 1 = \angle 5 \nonumber \]and\[ \angle 1 = \angle 4. \nonumber \]Hence,\[ \angle 5 = \angle 4. \nonumber \]Since our choice of angles was arbitrary, this shows that alternate interior angles are always congruent.

Example \( \PageIndex{ 3 } \)

The parallelogram \(A B C D\) shown below is formed by the intersection of two sets of parallel lines. Show that the opposite angles of the parallelogram are equal.

Solution

Angles 1 and 2 are equal because they are alternate interior angles, and angles 2 and 3 are equal because they are corresponding angles. Therefore, angles 1 and 3, the opposite angles of the parallelogram, are equal. A similar argument shows that angles 4, 5, and 6 are equal.

Checkpoint \(\PageIndex{3}\)

In the figure from Example \( \PageIndex{ 3 } \), suppose \( \angle 1 = 83^{ \circ } \). Find each of the following angular measures.

1. \( \angle 2 \)
2. \( \angle 5 \)
3. \( \angle 4 \)
4. \( \angle 3 + \angle 6 \)

Answer

1. \( 83^{ \circ } \)
2. \( 97^{ \circ } \)
3. \( 97^{ \circ } \)
4. \( 180^{ \circ } \)

Circles

A circle is defined to be the shape created from all points in a plane that are at a given distance (called the radius) from a given point (called the center).

Figure \( \PageIndex{ 13 } \): A circle with center \( O \) and radius \( r \)

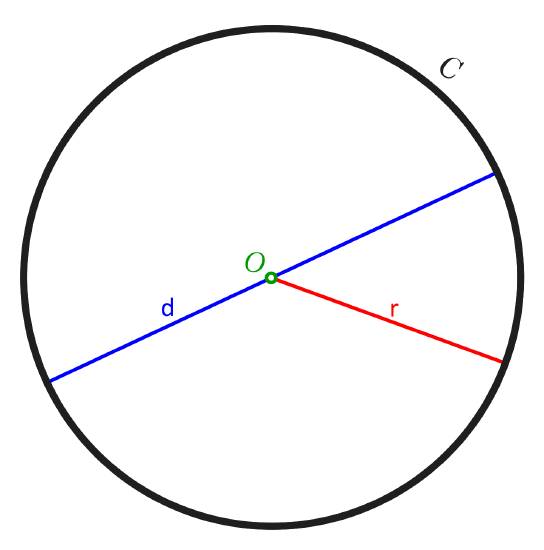
Figure \( \PageIndex{ 13 } \) shows a circle of radius \( r \) centered at a point \( O \). In fact, the word "radius" plays two roles in Geometry. Most people think of the radius as the distance between the center of a circle and its edge - this is true; however, any line segment joining the center of a circle with any single point on the circle itself is called a radius. Therefore, the word radius simultaneously refers to a distance and a line segment.

Just like the radius, the diameter of a circle, denoted as \( d \) in Figure \( \PageIndex{ 13 } \), has two interpretations. It is a line segment whose endpoints lie on the circle and that passes through the center and it is the length of such a line segment. The diameter the largest distance between any two points on the circle. Its length is twice the length of a radius. That is,\[ d = 2r. \nonumber \]

The terminology from Geometry related to circles extends beyond center, radius, and diameter (e.g., arc, chord, sector, and tangent); however, we will introduce these only as needed.

Circumference

The circumference is the distance around a circle, denoted as \( C \) in Figure \( \PageIndex{ 13 } \). It is proportional to the circle's radius.²

Theorem: Circumference

The circumference of a circle of radius \(r\) is given by\[C=2 \pi r.\nonumber \]

Proof

While a proof of this fundamental theorem in mathematics is beyond the scope of this course, it can be justified by the professor. It is fun and relatively easy to do (however, it requires the assumption that a circle's area is \( \pi r^2 \)).

Language Note: "Circumference of a Circle" is Redundant

It is common to hear someone say, "the circumference of a circle." However, the word circumference only applies to circles. Therefore, saying "the circumference of a circle" is redundant. For noncircular two-dimensional shapes, we use the word perimeter.

The number \(\pi \approx 3.14159\) is an irrational number that represents the ratio of the circumference of any circle to its diameter.

Example \(\PageIndex{4}\)

Loi buys a ring light for her YouTube videos. The light is circular and has a radius of 7 inches. What is the circumference of her ring light?

Solution

We are given the fact that the radius is 7 inches. Therefore, \( r = 7 \) (inches). Using the formula for circumference, we find that Loi's ring light has a circumference of\[ C = 2 \pi r = 2 \pi (7 \text{ inches}) = 14 \pi \text{ inches} \approx 44 \text{ inches}. \nonumber \]

Checkpoint \(\PageIndex{4}\)

Find the radius of a 100-meter circular race track. Round your answer to one decimal place.

Answer

\( r \approx 15.9 \) meters

Area of a Circle

The area of a circle is proportional to the square of its radius.

Theorem: Area of a Circle

The area of a circle of radius \(r\) is given by\[A=\pi r^2.\nonumber \]

Proof

Again, this proof is beyond the scope of this course; however, it can be justified by assuming the formula for the circumference (ask your instructor).

Example \(\PageIndex{5}\)

Phuong is making a circular tablecloth for her grandfather's antique oak table. If she wants the tablecloth to have a diameter of at least 7 feet (the bare minimum to cover the table), but no more than 9 feet (allowing a little bit of tablecloth to hang over the edge of the table), between what two values must the area of the tablecloth be? Round your answers to the nearest tenth of a square foot.

Solution

To barely cover the table, Phuong needs a tablecloth with radius 3.5 feet. Therefore, the minimum area of the tablecloth should be\[ A_{\text{minimum}} = \pi r_{\text{minimum}}^2 = \pi (3.5)^2 \approx 38.5 \text{ square feet}. \nonumber \]At most, if she wants a little bit of the tablecloth to hang over the edge, Phuong will want the radius to be 4.5 feet. This leads to an area of\[ A_{\text{maximum}} = \pi r_{\text{maximum}}^2 = \pi (4.5)^2 \approx 63.6 \text{ square feet}. \nonumber \]Any amount of circular tablecloth between 38.5 and 63.6 square feet should work nicely for Phuong's project.

Checkpoint \(\PageIndex{5}\)

If Piyali has a circular tablecloth with area 35 square feet, what is the diameter of the tablecloth?

Answer

6.7 feet.

---

Footnotes

¹ Mathematics is full of fascinations for the casual observer. The universal constant \( \pi \) is one such object. \( \pi \) is the ratio of the circumference of a circle to its diameter. That is,\[ \pi = \dfrac{C}{d} \nonumber \]for every circle in the universe - no matter how large or how small! This incredibly fascinating fact has made \( \pi \) a famously mysterious number.

² It would be more impactful, and still correct, to state the circumference of a circle is proportional to its diameter. That is,\[ C = \text{ some number }\times d. \nonumber \]It turns out that the value of "some number" (which is commonly called the constant of proportionality) is the universal constant \( \pi \). That is,\[ C = \pi d. \nonumber \]

---

Skills Refresher

The following is a set of review exercises you will need for this section.

Skills Refresher

For Problems 1 - 4, solve the equation.

1. \(x-8=19-2 x\)

2. \(2 x-9=12-x\)

3. \(13 x+5=2 x-28\)

4. \(4+9 x=-7+x\)

For Problems 5 and 6, solve the system.

5. \( \begin{cases}
   5x - 2y & = & -13 \\
   2x + 3y & = & -9 \\
   \end{cases}\)

6. \( \begin{cases}
   4x + 3y & = & 9 \\
   3x + 2y & = & 8 \\
   \end{cases}\)

Answers

1. \(9\)

2. \(2\)

3. \(-3\)

4. \(-2\)

5. \(x=-3,y=-1\)

6. \(x=6,y=-5\)

---

Homework

Vocabulary Check

1. When two rays share a common initial point they form a(n) ___.

2. Trigonometry focuses on oriented angles. An oriented angle starts from an ___ side and ends at a ___ side.

3. ___ angles start at an initial side and rotate clockwise to the terminal side.

4. A positive angle opens with a ___ rotation.

5. We define ___ measure by dividing the full rotation around the circle into 360 segments.

6. One-quarter of a complete revolution around a circle forms a ___ angle, which measures ___ degrees.

7. ___ angles measure between \( 0^{ \circ } \) and \( 90^{ \circ } \), while ___ angles measure between \( 90^{ \circ } \) and \( 180^{ \circ } \).

8. The degree system for measuring the size of an angle is also known as the ___ system.

9. When two lines intersect, the non-adjacent angles formed from this intersection are called ___ angles.

10. A line intersecting two parallel lines is called a ___.

11. The set of all points equidistant to a single point on a plane is called a ___.

12. The ___ of a circle is simultaneously the largest distance between any two points on a circle and is the name of the line segment that passes through the center of the circle whose endpoints lie on the circle.

13. \( \pi \) is a(n) ___ number (unlike \( 3 \), which is a natural number).

Concept Check

14. Greek letters like \( \alpha \), \( \beta \), and \( \theta \) are often used to represent angles in Trigonometry. Name one Greek letter that is never used as a label for an angle.

15. If a positive angle rotates from its initial to its terminal side, what direction is the rotation?

16. If a negative angle rotates from its initial to its terminal side, what direction is the rotation?

17. Suppose you have a straight angle and you subtract a right angle. What type of angle is the result?

18. Can a right angle be acute? How about obtuse?

19. Suppose the vertex of an angle is at the point \( P \), and the points \( R \) and \( S \) lie on the initial and terminal sides of the angle, respectively. Which of the following are correct notations for the angle?

    1. \( \angle P \)

    2. \( P \)

    3. \( m \angle P \)

    4. \( \triangle P \)

    5. \( \angle PRS \)

    6. \( \angle RPS \)

    7. \( \angle SPR \)

20. Quantities measured in degrees use the ___ symbol.

21. According to this text, can \( 107^{ \circ } \) have a complement? If so, what is the value of this complement?

22. According to this text, can \( 107^{ \circ } \) have a supplement? If so, what is the value of this supplement?

23. Can two acute angles be supplementary?

24. Choose two of the eight angles formed by a pair of parallel lines cut by a transversal. Those two angles are either equal or ___.

25. Write two formulas for the circumference of a circle - one involving the radius of the circle and the other involving the diameter.

26. The formula for the circumference of a circle is ___.

27. The formula for the area of a circle is ___.

True or False? For Problems 28 - 36, determine if the statement is true or false. If true, cite the definition or theorem stated in the text supporting your claim. If false, explain why it is false and, if possible, correct the statement.

28. If \( \alpha \) and \( \beta \) are vertical angles, then \( \alpha + \beta = 90^{ \circ } \).

29. The complement to \( 47^{ \circ } \) is \( 43^{ \circ } \).

30. The supplement to \( 190^{ \circ } \) is \( -10^{ \circ } \).

31. Alternate interior angles sum to \( 180^{ \circ } \).

32. The distance from the center to the edge of a circle is called the radius of the circle.

33. The line connecting the center of a circle to its edge is called a radius.

34. The circumference of a square is the sum of the lengths of its sides.

35. \( \pi = 3.14 \)

36. \( \pi = \frac{22}{7} \)

Basic Skills

For Problems 37 - 45, state (if possible) which angles are acute and which are obtuse. Give the complement and the supplement of each angle, if applicable.

37. \( 30^{ \circ } \)

38. \( 45^{ \circ } \)

39. \( 60^{ \circ } \)

40. \( 43^{ \circ } \)

41. \( 90^{ \circ } \)

42. \( 120^{ \circ } \)

43. \( 135^{ \circ } \)

44. \( 143^{ \circ } \)

45. \( 150^{ \circ } \)

For Problems 46 - 51, give the complement of each angle.

46. \(60^{\circ}\)

47. \(80^{\circ}\)

48. \(25^{\circ}\)

49. \(18^{\circ}\)

50. \(64^{\circ}\)

51. \(47^{\circ}\)

For Problems 52 - 57, give the supplement of each angle.

52. \(30^{\circ}\)

53. \(45^{\circ}\)

54. \(120^{\circ}\)

55. \(25^{\circ}\)

56. \(165^{\circ}\)

57. \(110^{\circ}\)

For Problems 58 and 59, arrows on a pair of lines indicate that they are parallel. Find \(x\) and \(y\).

58. 
    
59. 
    

60.  

    1. Among the angles labeled 1 through 5 in the figure below, find two pairs of equal angles.

       

    2. \(\angle 4+\angle 2+\angle 5= \)_________.

    3. Use parts (a) and (b) to explain why the sum of the angles of a triangle is \(180^{\circ}\).

61. \(A B C D\) is a rectangle. The diagonals of a rectangle bisect each other. In the figure, \(\angle A Q D=130^{\circ}\). Find the angles labeled 1 through 5 in order, and give a reason for each answer.

    

For Problems 62 and 63, give an exact answer, and round your answer to hundredths.

62. What is the area of a circle whose radius is 5 inches?

63. What is the circumference of a circle whose radius is 5 meters?

For Problems 64 - 67, find the circumference and area for each circle having the given radius \( r \) or diameter \( d \).

64. \( r = 7 \text{ feet} \)

65. \( r = 8.4 \text{ centimeters} \)

66. \( d = 16 \text{ yards} \)

67. \( d = 12 \text{ meters} \)

68. Find the diameter of a circle having a circumference of \( 4\pi \) kilometers.

69. Find the radius of a circle having a circumference of \( 10 \) inches.

70. Find the radius of a circle having an area of \( 24\pi \) square meters.

71. Find the diameter of a circle having an area of \( 64 \) square feet.

72. Find the circumference of a circle having an area of \( 81\pi \) square miles.

Synthesis Questions

73. State the condition(s) for which \( \alpha \) is an acute angle, and for which \( \alpha \) is an obtuse angle. In each case, give the complement and the supplement of \( \alpha \).

For Problems 74 - 77, arrows on a pair of lines indicate that they are parallel. Find \(x\) and \(y\).

74. 
    
75. 
    
76. 
    
77. 
    

78. Climbing Stairs. In each of the following problems, refer to the following image of a staircase and rails. Assume the rails are perpendicular to the ground, they are parallel to each other, and that the top rail (handrail) is parallel to the bottom rail (the black line along the steps).

    

    1. What is the relationship between \( \alpha \) and \( \beta \)?

    2. What is the relationship between \( \beta \) and \( \theta \)?

    3. What is the relationship between \( \beta \) and \( \phi \)?

    4. What is the relationship between \( \theta \) and \( \phi \)?

    5. Find \( \alpha \) if \( \beta = 48^{ \circ } \).

    6. Find \( \theta \) if \( \alpha = 30^{ \circ } \).

Applications

79. Emergency Light. An ambulance has a rotating light on its roof. The light rotates through one complete revolution every 2 seconds. How long does it take the light to rotate through \( 90^{ \circ } \)?

80. Rotation of the Earth. The Earth goes through a complete circuit around the sun in approximately 365.25 days. Through how many degrees does the Earth move in one week?

81. Earth's Rotation About the Sun. The Earth takes 24 hours to make a complete rotation on its axis. If your math class is 2 hours and 20 minutes, through how many degrees does the Earth turn during your math class?

82. Circumference of the Earth. The radius of the Earth is approximately 3,960 miles. Using this approximation, find the circumference of the Earth.

83. Earth's Rotation About the Sun. The Earth has a nearly circular orbit about the sun. The radius of this near-circular orbit is approximately 93 million miles. Find the distance the Earth travels when it completes one full orbit about the sun.