1.2: Book 1 Definitions
( \newcommand{\kernel}{\mathrm{null}\,}\)
- A point is that which has no part. [Essentially meaningless as a definition. From a modern perspective, there must be some undefined terms. This is one.]
- A line is breadthless length. [Again, this is no definition. It is another undefined term.]
- The extremities of a line are points. [Endpoints. Formally, something about "betweenness".]
- A straight line is a line which lies evenly with the points on itself. [Say what? Curves are "lines" here but what is "straight"? In Chapter 5, we will define it formally but it won’t seem natural!]
- A surface is that which has length and breadth only. [A region in the (plane) geometry.]
- The extremities of a surface are lines. [Edges of a polygon or polyhedron are line segments.]
- A plane surface is a surface which lies evenly with the straight lines on itself. [See the above.]
- A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line. [Modern? An angle is the union of two rays with a common initial point.]
- And when the lines containing the angle are straight, the angle is called rectilineal. [As opposed to an angle determined by the intersection of two "smooth" curves; i.e. the intersection of their tangents at the point of intersection. We will need these in the "Poincaré disk model" for hyperbolic geometry.]
- When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands. [Modern? Perpendicular lines are lines that intersect to form congruent, adjacent angles. The angles they form are called right angles.]
- An obtuse angle is an angle greater than a right angle. [A real definition.]
- An acute angle is an angle less than a right angle. [Two in a row!]
- A boundary is that which is an extremity of anything. [Your sarcasm here?]
- A figure is that which is contained by any boundary or boundaries. [I.e., closed and bounded.]
- A circle is a plane figure contained by one line [curve] such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another. [Another, "Say what?"!]
- And the point is called the center of the circle. [Another real definition!]
- A diameter of the circle is any straight line drawn through the center and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle. [Omit "circumference”.]
- A semicircle is the figure contained by the diameter and the circumference cut off by it. And the center of the semicircle is the same as that of the circle. [As in #17, "circumference" implies the circle itself, the set of points equidistant from a given point; circumference actually means the linear measure of the circle.]
- Rectilineal figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines. [Real definitions but we’d say polygon and, in case of three, triangle, but trilateral is used as is quadrangle and n-gon if we wish to specify the number of sides, n.]
- Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.
- Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute angled triangle that which has its three angles acute. [For us, right triangle, obtuse triangle, and acute triangle.]
- Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not [necessarily] equilateral; a rhombus that which is equilateral but not [necessarily] right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia. [Never used!]
- Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction. [Do they exist? Yes (but not in elliptic geometry), but what does "infinite" mean? Formally, it is the Archimedean Property: Given two segments, enough copies of the shorter one exceeds the longer one (independent of their lengths.]
Postulates. [Axiom and postulate are interchangeable terms from the modern perspective, statements accepted as true without proof. Not in some universal sense, only in the context under consideration]
Let the following be postulated:
- To draw a straight line from any point to any point. [Hereafter, Axiom 1: Two points determine...]
- To produce a finite straight line continuously in a straight line. [Lines are "infinite" - Subsumed under the Ruler Postulate]
- To describe a circle with any center and distance. [Axiomatically, a point and a radius determine a unique circle and circles behave as they should. ’Nuff said.]
- That all right angles are equal to one another. [Subsumed under the Protractor Postulate.]
- That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles. [Euclid’s 5th Postulate, traditional form. Far more common is Playfair’s form: Given a line and a point not on the line, there is at most one line on the given point that is parallel to the given line. At most one? Maybe not even one?! No, but by proof, not by axiom].
Common Notions [From a modern perspective, these follow from set theory and properties of real numbers that can also be developed axiomatically. If we were to do so, we would never get done!]
- Things which are equal to the same thing are also equal to one another. [Read: Congruence is transitive.]
- If equals be added to equals, the wholes are equal.
- If equals be subtracted from equals, the remainders are equal.
- Things which coincide with one another are equal to one another.
- The whole is greater than the part.
Proposition 1. On a given finite straight line to construct an equilateral triangle.
[Note the use of the infinitive as a command, "to construct". Think ancient Latin (or modern Spanish). Also "finite straight line" means line segment.]
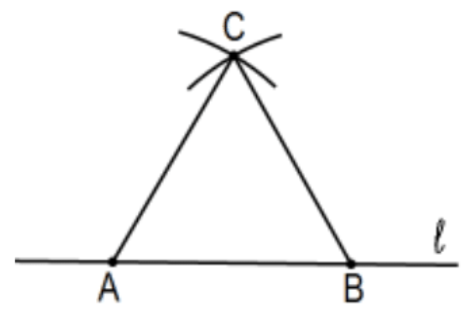
Construction: Choose any 2 points on the line, say A and B. Let C be the intersection of circles (A; AB) and (B; AB), the circles centered at A and B both of radius AB (only one of the two intersections of these two circles to be more precise). The triangle determined by the 3 points, △ABC is equilateral.
Proof: By construction, all 3 sides are congruent, the definition of equilateral. [But how do we know the circles have to intersect? Can they "slip through" one another without intersecting? No, but there are geometries where they might. Without bothering to state them, we assume (as did the Greeks) that our axioms assure validity of such "continuity" considerations.]
Proposition 2. To place at a given point (as an extremity) a straight line equal to a given straight line
As stated, this really means "to construct"; i.e., use a compass to copy a line segment at any point on another line. It’s immediate from the Ruler Postulate; exactly one point (with direction) for any given length.
Proposition 3. Given two unequal straight lines, to cut off from the greater a straight line equal to the less. [This is also part of the Ruler Postulate so nothing to prove, at least from a modern viewpoint.]
Proposition 4. If two triangles have the two sides equal to two sides respectively, and have the angles contained by the equal straight lines equal, they will also have the base equal to the base, the triangle will be equal to the triangle, and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend. [That is, Side-Angle-Side (SAS) that we will assume as our triangle congruence axiom. It is proved in Book 1 but "superposition", the underlying assumption of the ancient Greek proof, is tantalizingly obvious so don’t blame the Greeks too much for not realizing the need for an axiom; in our case, the SAS Axiom.]
Proposition 5. In isosceles triangles, the angles at the base are equal to one another, and, if the equal straight lines be produced further, the angles under the base will be equal to one another.
[See the Introduction and the introduction to this chapter and say "the base angles are congruent."]
Proposition 6. If in a triangle two angles be equal to one another, the sides which subtend the equal angles will also be equal to one another. [The converse of the "base angles of an isosceles triangle theorem"; as usually stated: In a triangle, sides opposite congruent angles are congruent.]
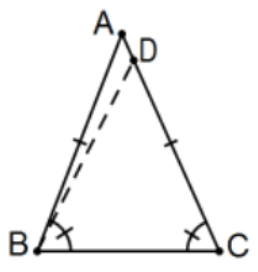
Given: △ABC with ∠B≅∠C Prove: _AB≅AC.
Proof: Take D to be the point along ray CA with CD≅BA (by the Ruler Postulate). Now △DCB≅△ABC by SAS so ∠DBC≅∠ACB by cpctc and, by hypothesis and transitivity, ∠DBC≅∠ABC. By the Protractor Postulate, ray BD is the same ray as BA so, by the Ruler Postulate again, D=A (exactly the same point!), and CA≅BA just by renaming CD as CA. QED.
Proposition 7. Given two straight lines constructed on a straight line (from its extremities) and meeting in a point, there cannot be constructed on the same straight line (from its extremities), and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each to that which has the same extremity with it. [This, together with Prop 8, is usually known as the Side-Side-Side CongruenceTheorem (SSS). Formally, if two triangles have three pairs of sides congruent, the triangles themselves are congruent.]
Proposition 8 (SSS). If two triangles have the two sides equal to two sides respectively, and have also the base equal to the base, they will also have the angles equal which are contained by the equal straight lines.
Given: AB≅EF,AC≅EG,BC≅FG
Prove: △ABC≅△EFG
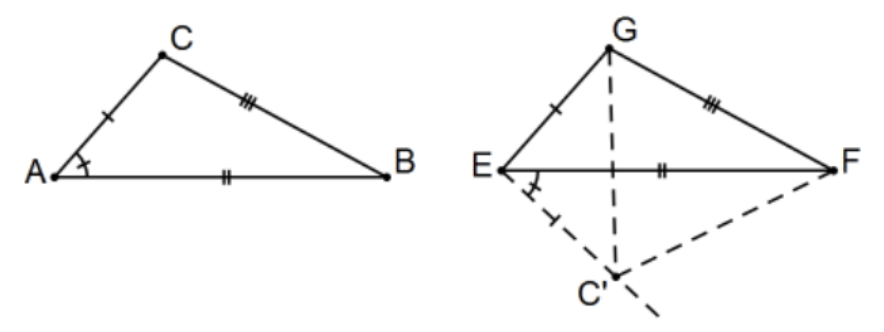
Proof: Copy ∠A at E but on the opposite side of line EF than G (Protractor Postulate). Along that ray, let C′ be the point such that EC′≅AC so, by the given hypothesis and transitivity, △EC′G is isosceles with base angles at C′ and G. Moreover, △ABC≅△EFC′ by SAS so FC′≅BC by cpctc so △FGC′ is also isosceles, also with base angles at C′ and G. Adding congruent angles, we have ∠EC′F≅∠EGF. Thus △EFC′≅△EFG by SAS and △ABC≅△EFG by transitivity. QED.
As long as it is done logically, there is nothing magic about following Euclid’s Elements Book 1 in its original sequence and it is convenient to look at Prop 23 at this point:
Proposition 23. On a given straight line and at a point on it to construct a rectilineal angle equal to a given rectilineal angle. [That is, copy an angle using straightedge and compass.]
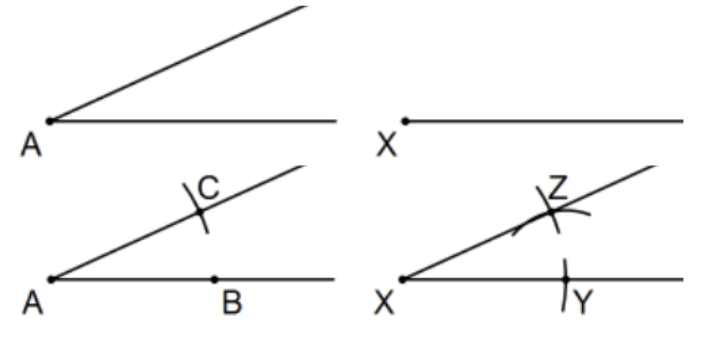
Construction: To copy ∠A at point X on the side given, choose any point B≠A on one of the rays of ∠A an use that as the radius for circles centered at A and at X to establish points C and Y and an arc in the vicinity of (not yet determined Z ) Construct the circle with center at Y of radius BC to establish point Z. Ray XZ is the desired angle at point X.
Proof: △ABC≅△XYZ by SSS so ∠A≅∠X by cpctc. QED.
Proposition 9. To bisect a given rectilinear angle.
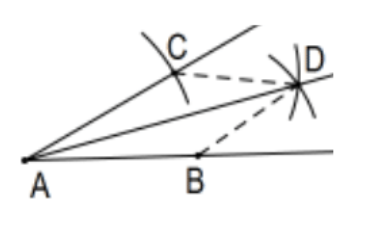
Construction: Choose a point, say B, on one of the rays of the angle and determine point C on the other ray by constructing the circle (A;AB), the circle with center A of radius AB. With length r>(1/2)m(BC), construct circles (B;r) and (C;r) and let D be their point of intersection (farthest from A, as pictured). Ray AD is the desired angle bisector. [Do NOT construct (or even indicate) segments BD and CD or any such dashed segments in these constructions; they are only indicated to clarify the proof.]
Proof: △ABD≅△ACD by SSS so that ∠BAD≅∠CAD by cpctc and, by definition of angle bisector, we’re done. [Why not until now? In fact, there is an SAS proof for this so that it could have been done before SSS. Can you see it?]
QED.
Proposition 10. To bisect a given finite straight line. [That is, construct the midpoint of a line segment.]
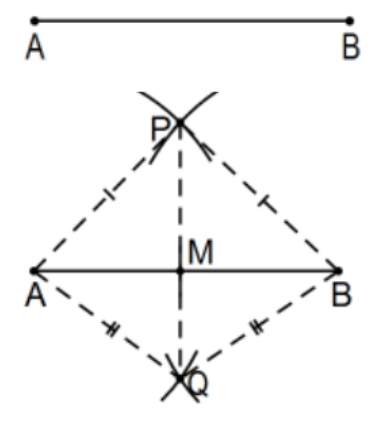
Construction: [Note: This does not say the perpendicular bisector, only the point that bisects; i.e., the midpoint. After the traditional construction, the perpendicular bisector of the segment to determine its midpoint, we will look at another that emphasizes this point. The problem is that some of you will say "perpendicular bisector" when you only mean one of "perpendicular" or "bisector". Words have meaning so use them correctly and meaningfully.]
By means of circles, of the same radii, each greater than (1/2)m(AB), construct two points, each equidistant from the endpoints; in this case, A and B are the endpoints and P and Q are the points, each equidistant from A and B. Finally, let M be the intersection of lines AB and PQ. [As in Prop 9, DON’T include the pictured dashed segments, only the construction. They are only there for clarity in the proof.]
Proof: By SSS, △APQ≅△BPQ so that ∠APQ≅∠BPQ by cpctc. [Note: More clever would’ve been to say "From the proof of Prop 9 , we have ∠APQ≅∠BPQ. Can you see it?] In any case, we now have △APM ≅△BPM by SAS so that AM≅BM by cpctc and M is the midpoint of AB. QED.
Note: A useful extension of the proof above is:
Theorem: A point is on the perpendicular bisector of a line segment if and only if it is equidistant from each of its endpoints (PS 1, #20).]
[As promised, here is a construction you probably would not have thought of that we can’t prove yet but only because we don’t yet have AAS or congruence of vertical angles. If we did...
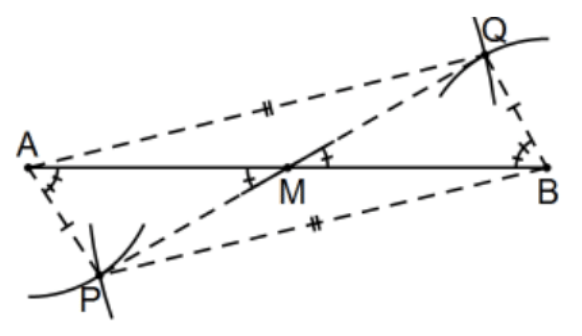
Construction: Consider two pairs of circles with centers A and B of the same radii large enough to intersect at points P and Q. Let M be the intersection of lines AB and PQ; then M is the desired point.
Proof: △ABQ≅△BAP by SSS so ∠ABQ≅∠BAP by cpctc. But ∠ABQ=∠MBQ (i.e., exactly the same angle) and ∠BAP=∠MAP with ∠AMP≅∠BMQ because they are vertical angles. Now △AMP≅△BMQ by AAS and, by cpctc, AM≅BM as desired. QED.]
Proposition 11. To draw a straight line at right angles to a given straight line from a given point on it. [Construct a perpendicular at a given point on a given line. Note: Do not use the other intersection of these two circles. Why not? Is PQ the only perpendicular to the line on the point P? Yes. Why?]
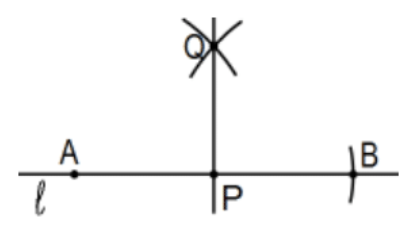
Proof: See PS 1, #9.
Proposition 12. To a given infinite straight line, from a given point which is not on it, to draw a perpendicular straight line. [Construct a perpendicular to a line from a point not on the line. Is it the perpendicular to the line on the point? Not yet; not until after Prop 16.]
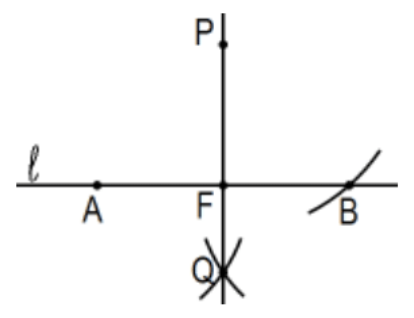
Proof: See PS 1, #8.
Proposition 13. If a straight line [ray] set up on a straight line make angles, it will make either two right angles or angles equal to two right angles. [Nothing to prove; it is axiomatic by the Protractor Postulate.]
Proposition 14. If with any straight line, and at a point on it, two straight lines not lying on the same side make the adjacent angles equal to two right angles, the two straight lines will be in a straight line with one another. [Here either. It is also a consequence of the Protractor Postulate.]
Proposition 15. If two straight lines cut one another, they make the vertical angles equal to one another.
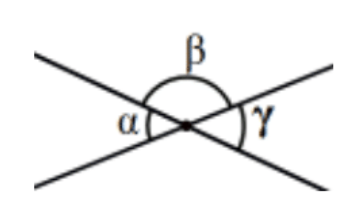
Proof: Viewed most simply: α+β=180∘=β+γ implying α=γ. QED.
Proposition 16. [Exterior Angle Theorem (neutral geometry form). KNOW IT!] In any triangle, if one of the sides be produced, the exterior angle is greater than either of the nonadjacent interior angles.
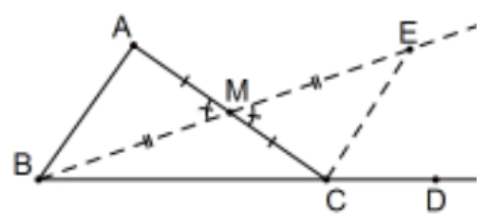
Proof: Let ray BM be the median on B [ M is the midpoint of segment AC] and let E be along that ray such that EM≅BM. Conclude that ∠A≅∠ACE<∠ACD. Why does this prove that ∠B<∠ACD? QED.
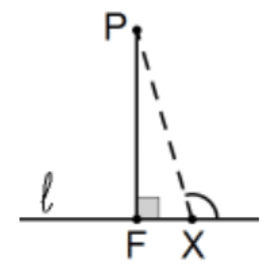
Corollary: The line of Prop 12 is unique. It is the line on the point that is perpendicular to the line.
Other immediate corollaries are Props 17 and 27. Some others are only a step away.
Proposition 17. In any triangle, two angles taken together in any manner are less than two right angles.
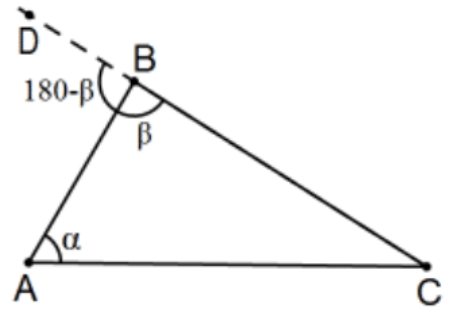
Proof: We focus on two of the angles, specifically those at A and B, of △ABC. By supplementary angles, m(∠CBA)+m(∠ABD)=β∘+(180−β)∘ where ∠ABD is a nonadjacent exterior angle to ∠A so, by Prop. 16 , m(∠A)<m(∠ABD) and α+β<(180∘−β)+β=180∘. Finally, α+β<180∘
Proposition 18. In any triangle, the greater side subtends the greater angle. [Angles opposite greater sides are greater. Note: Be careful which is which.]
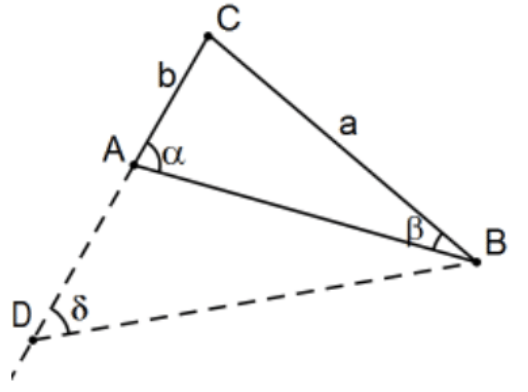
Proof 1: In △ABC, assume a>b. Prove that α>β.
Extend ray CA to point D such that CD≅CB. Then ∠D≅∠CBD (they are base angles of a triangle constructed to be isosceles) and point A is in the interior of ∠CBD making ∠CAB an exterior angle wrt (with respect to) ∠ADB of △ADB. By the Exterior Angle Theorem and the fact that ∠A=∠CAB, we have that δ<α, and, since point A is interior to ∠CBD,m(∠B)(=∠CBA)<m(∠CBD). By transitivity, we have m(∠B)<m(∠A) or α>β. QED.
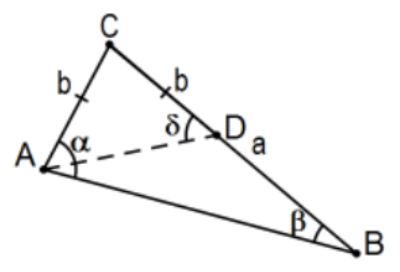
Proof 2: As above, in △ABC, assume a>b. This time, let D be along ray CB such that CD≅CA and proceed similarly. QED.
Proposition 19. In any triangle, the greater angle subtends the greater side. [The converse of #18; i.e., sides opposite greater angles are greater. Again, if..., then...?]
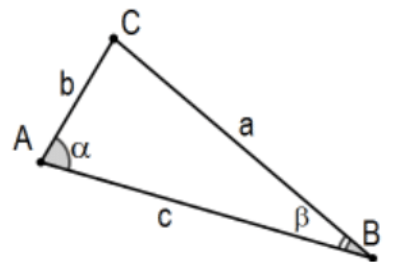
Proof: In △ABC pictured as in Prop.18 but assume that ∠A>∠B. There are only three possibilities, a<b,a=b, or a>b. In the second case, the triangle would be isosceles and its base angles congruent, a contradiction to the hypothesis. In the first case, applying Prop 18, we would have that ∠A<∠B; again, a contradiction. Thus a>b. QED.
Note: Here, proof of the original statement made a proof of its converse to be very easy. Often that is the case (when the converse is true) but not necessarily. Sometimes a proof of the converse of statement can be quite different from using the validity of the original statement
Corollary: The shortest distance from a point to a line is the perpendicular distance.
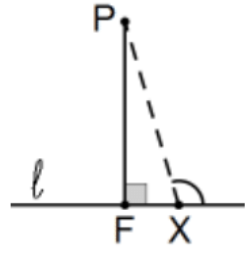
Proof: Let F be the foot of the perpendicular on P and let X be any other point on the line. The greatest angle in the resulting triangle is... QED.
Proposition 20 [Triangle Inequality.] In any triangle, two sides taken together in any manner are greater than the remaining one. In other words, the shortest distance between any two points is (surprise, surprise) the length of the line segment that joins them.
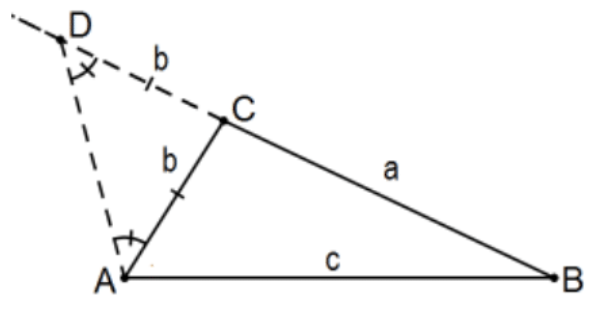
Proof: In the picture, we prove that a+b>c. Let D be the point along ray BC of length b making △ACD to be an isosceles triangle so that ∠D≅∠DAC. It is clear that ∠DAC<∠DAB so that ∠ADB<∠DAB. By Prop 19, AB <BC+CD. That is, a+b>c. QED.
Proposition 21. If on one of the sides of a triangle, from its extremities, there be constructed two straight lines meeting within the triangle, the straight lines so constructed will be less than the remaining two sides of the triangle, but will contain a greater angle.
Note: The archaic language is a little hard to understand but the idea is quite simple. In any triangle △ABC, the triangle inequality says that the shortest distance between the two points A and C is the line segment that joins them. This proposition says that "going through" any interior point D of the triangle is shorter than following the sides of the triangle through B and that the angle determined is greater than the angle at that third point B.
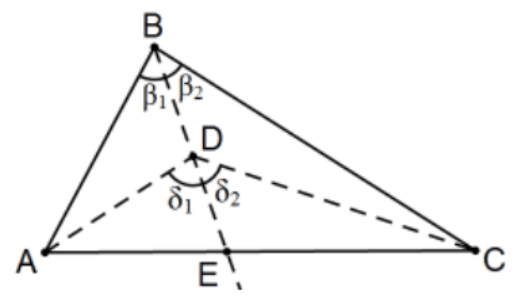
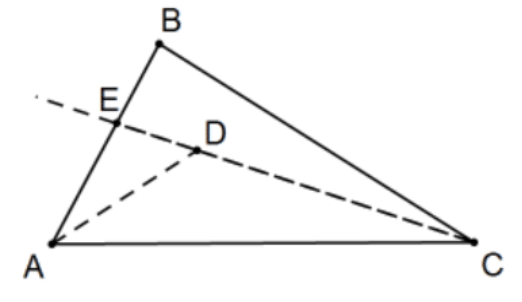
Proof: The angle situation is the easier of the two. Just consider ray BD and use the EAT at D by dividing the angle at B into two angles of size β1 and β2 using ray BD that also divides ∠ADC into two angles of size δ1 and δ2 with both β1<δ1 and β2<δ2 by the exterior angle theorem and adding, β=β1+β2<δ1+δ2=δ so ∠ABC<∠ADC. For the "shorter path" conclusion, extend ray CD to determine point E as pictured. The result follows from careful use of the Triangle Inequality: AD<AE+ED so that AD+DC<(AE+ED)+DC and reassociating, AD+DC<AE+(ED+DC)=AE+EC. But also EC<EB+BC so that AE+EC<AE+(EB+BC) and, since AE+EB=AB, we have that AD+DC<AB+BC.
Proposition 22. Out of three straight lines, which are equal to three given straight lines, to construct a triangle: thus it is necessary that two of the straight lines taken together in any manner should be greater than the remaining one. [The archaic language is awkward but the idea is simple.]
Proposition 23. Copying an angle using straightedge and compass was done immediately after Prop 8.
Proposition 24. If two triangles have the two sides equal to two sides respectively, but have the one of the angles contained by the equal straight lines greater than the other, they will also have the base greater than the base. [The Hinge Theorem, along with its converse Prop 25.]
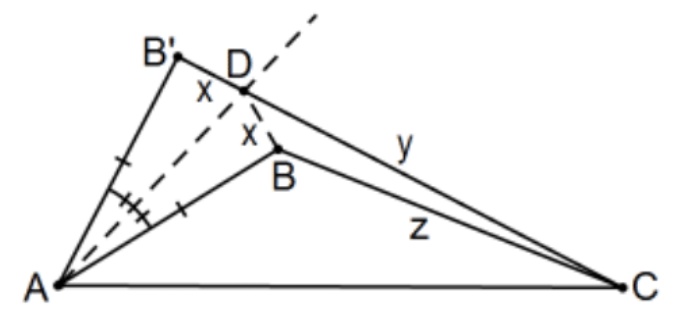
Proof: In the figure, AB≅AB′ and ∠BAC<∠B′AC.
Prove BC<B′C, or more simply, x+y>z.
Bisect ∠BAB′ to determine point D and △BAD≅△B′AD by SAS so BD≅B′D. But BD+DC>BC so we’re done. The picture could be misleading in that AD could shorter than AB but the proof is the same. QED.
Proposition 25. If two triangles have the two sides equal to two sides respectively, but have the base greater than the base, they will also have the one of the angles contained by the equal straight lines greater than the other. [The converse of Prop 24 and easily follows from it.]
Proposition 26. If two triangles have the two angles equal to two angles respectively, and one side equal to one side, namely, either the side adjoining the equal angles, or that subtending one of the equal angles, they will also have the remaining sides equal to the remaining sides and the remaining angle to the remaining angle. [Both ASA and AAS. These are different theorems with different proofs so a mild structural error!]
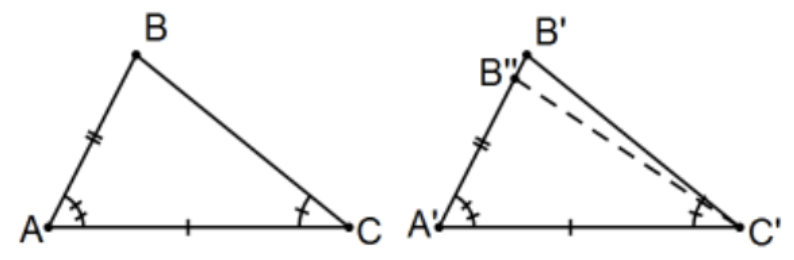
Proof of ASA: Assume ∠A≅∠A′,∠C≅∠C′, and AC≅A′C′. Let B′′ be along ray A′B′ such that AB≅A′B′′. Then △ABC≅△A′B′′C′bySAS so ∠C≅∠A′C′B′′ by cpctc and, by transitivity, ∠C′=∠A′C′B′′; i.e., one and the same angle. Therefore, B′=B′′ and the desired triangles are already known to be congruent. QED.
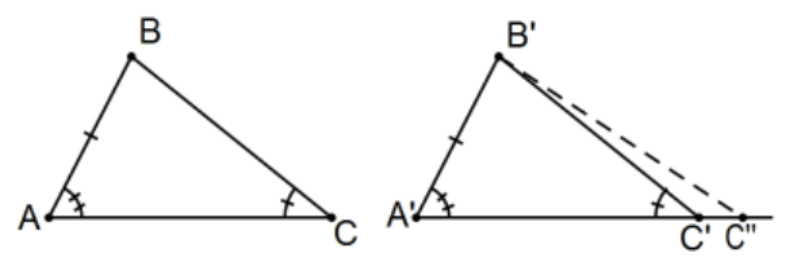
Proof of AAS: Assume ∠A≅∠A′,∠C≅∠C′, and AB≅A′B′. Let C′′ be along ray A′C′ such that AC≅A′C′′. Then △ABC≅△A′B′C′′ by SAS so ∠C≅∠C′′ by cpctc. If C′≠C′′,ΔB′C′′C′ would be a non-degenerate triangle and would therefore violate the Exterior Angle Theorem. Since that is impossible, C′=C′′ and, as before, the triangles are already known to be congruent. QED.
Proposition 27. If a straight line falling on two straight lines make the alternate angles equal to one another, the straight lines will be parallel to one another. [With Prop 23, parallel lines exist!]
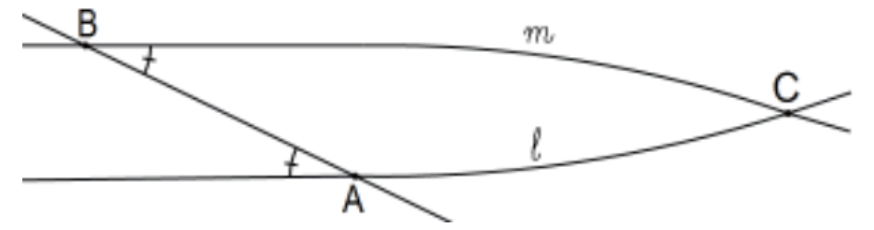
Proof: Suppose ∠A≅∠B but the lines ℓ and m intersect at C as pictured. Then ∠A would be an exterior angle not adjacent to interior angle ∠B with respect to △ABC. But by EAT,∠B<∠A so that is impossible. That is, there is no such intersection on the right side. The lines can’t intersect on the other side either for the same reason by interchanging which angle is interior and which is exterior. QED.
Proposition 28. If a straight line falling on two straight lines make the exterior angle equal to the interior and opposite angle on the same side, or the interior angles on the same side equal to two right angles, the straight lines will be parallel to one another. [Corollaries of Prop 27.]
Euclid’s Elements, Book 1, Prop 29 is the converse of Prop 27−8 and that would mean we’d be in Euclidean geometry since (along with the rest of the axioms we are assuming) it is logically equivalent to Euclid’s 5th Postulate and lots of variants some of which we’ll look at eventually. For now, we are focusing on neutral or, by another common name, absolute geometry. Although there are many later theorems in Euclid’s Elements (including in books that succeed Book 1) that are theorems of neutral geometry with identical proofs, the fact that Euclid went this far without using the 5th Postulate, including the limited form of the Exterior Angle Theorem, is persuasive indication that the Greeks were trying their best to prove it as a theorem instead of reluctantly accepting it as another axiom. For many centuries thereafter, very good geometers conducted extensive work in failed attempts to prove it. We will touch on a little of that in preliminary efforts of Saccheri and Lambert in the next chapter. Only the eventual acceptance of all of the other axioms along with the negation of Euclid’s 5th Postulate as a legitimate geometry in its own right, hyperbolic geometry, resolved the millennia-old problem now known as modern geometry.


