1.3: Problem Set 1

Exs 1-6 relate to the pictured isosceles triangle with base angles at B and C. In each, indicate in a corresponding sketch all given information in the standard manner and, equally important, nothing but the given information. Then prove the base angles are congruent freely using, as appropriate, any of the standard congruence statements SAS, SSS, ASA, AAS, and Hypotenuse-Leg.

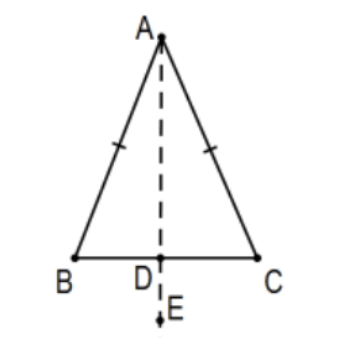
1. Assume that point \(\mathrm{D}\) is the point determined by ray \(\mathrm{AE}\), the bisector of \(\angle \mathrm{A}\).
2. Assume that point \(\mathrm{D}\) is the midpoint of line segment BC.
3. Assume that point \(\mathrm{D}\) is determined by the perpendicular from (on) point A to line BC.
4. Explain why the picture is misleading if you were to assume that line \(\mathrm{DE}\) is the perpendicular bisector of segment BC so that your ensuing proof would probably be flawed (i.e., not a proof at all).
5. Using only isosceles \(\triangle \mathrm{ABC}\) (that is, with no auxiliary points or lines) and SAS.
6. Using only isosceles \(\triangle \mathrm{ABC}\) (that is, with no auxiliary points or lines) and SSS.
7. Proposition 9 in Euclid’s Elements, Book 1, and is translated as, "To bisect a given rectilinear angle." Construct the bisector of an angle and prove that it is valid.
8. Construct a perpendicular line to a line from (or "on") a point which is not on the line and prove your construction is valid.
9. Construct a perpendicular line to a line on a point which is on the line and prove your construction. [Note: In both Exs 8 and 9, the indefinite article "a" is deliberate but, and as remarked in the text for different reasons, both lines are unique so "the".]
10. Definitions are crucial to mathematics even though I generally will not ask you to quote any of the standard ones of elementary Euclidean geometry. For each, state the essence of its definition; i.e., only the information known about the geometric figure or situation by definition. Include a sketch of a representative of each situation and indicate in it only the information given from its definition.

i. isosceles triangle xii. complementary angles xxiii. rhombus

ii. right angle xiii. supplementary angles xxiv. bisector

iii. rectangle \(\quad\) xiv. tangent line \(\quad x x v\). regular polygon

iv. scalene triangle \(\quad \mathrm{xv}\). concentric circles \(\quad\) xxvi. median

v. obtuse triangle xvi. trapezoid \(\quad\) xxvii. altitude

vi. right triangle \(\quad\) xvii. isosceles trapezoid \(\quad\) xxviii. concurrent lines

vii. square xviii. radius \(\quad\) xxix. skew lines

viii. parallel lines \(\quad\) xix. diameter \(\quad\) xxx. parallelogram

ix. vertical angles \(\quad\) xx. tangent circles \(\quad\) xxxi. Add your own!

x. perpendicular lines \(\quad\) xxi. incircle of a polygon (need not exist)

xi. polygon xxii. circumcircle of polygon (need not exist)

11. State (in modern, coherent, mathematical English) and prove Euclid’s Elements’ Proposition 6, the converse of the base angles of an isosceles triangle theorem.

12. State (in modern, coherent, mathematical English) and prove Euclid’s Elements’ Prop. 18, "In any triangle the greater side subtends the greater angle." Complete the indicated second proof.

13. State (in modern, coherent mathematical English) and prove Euclid’s Elements’ Prop. 19, the converse of the result in Ex \(12 .\)
14. Consider the statement: All squares are rectangles.

a. By the inclusive definition (the usual in mathematics), the statement is true. State it as an implication; that is, change the statement to "If p, then \(q\) " form.

b. State its converse as a formal implication and restate the implication in casual (common use) form.

c. Is it true? Prove your assertion.

15. Prove that the shortest distance from a point to a line is along the perpendicular.

16. A line is defined to be tangent to a circle if they intersect in exactly 1 point. Prove that a line that intersects a circle is tangent to the circle if and only if it is perpendicular to the radius that it determines.
17. Once again, Ex 9 says " \(a\) perpendicular from a point to a line", not "the perpendicular from a point to a line. Prove that the definite article is correct and argue that on a sphere such a line need not be unique. [Hint: The North Pole and the Equator can be helpful here.] It is "the" under the axioms of neutral geometry but this is somewhat subtle, a consequence of the Exterior Angle Theorem, Prop.16.]
18. Construct the copying of a triangle and prove that the construction is valid. [Note: This is not "duplicating that triangle"; that is archaic usage that means to double its area.]
19. A kite is a quadrilateral with two pairs of congruent adjacent sides (the shape of a traditional kite).

i. Prove that the diagonals of a kite are perpendicular.

ii. State a reasonable (i.e., smooth, non-artificial sounding) form of the converse of \(19 i\).

iii. Prove or disprove \(19 i i\).

21. Theorem: A point is on the perpendicular bisector of a line segment if and only if it is equidistant from each of its endpoints. Note: An alternate form for this theorem, especially in older books is, "The locus of all points equidistant from two points is the perpendicular bisector of the line segment that joins them.”
22. Given three points on a circle, construct the center of the circle.

Note 1: This language means more than it says; it means to explain a construction procedure and prove that your procedure is valid.

Note 2: Do not construct perpendicular bisectors of all 3 of the determined chords. Why not?

23. Part of Proposition 26 (both ASA and AAS) is better thought of as "If SAS, then ASA." State its converse and prove it. [Hint: See the comments on SSS at the end of the Introduction.]
24. A quadrilateral with the property that its four angles make two pairs of successive congruent angles (they share a side) is an isosceles trapezoid. Corollary: The opposite sides of a rectangle are congruent. [Hint: Consider the perpendicular bisector of either base and include diagonals to make congruent triangles.]