3.2: Other Quadrilaterals

Last updated
Save as PDF

Page ID: 34133

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In this section we will consider other quadrilaterals with special properties: the rhombus, the rectangle, the square, and the trapezoid.

Figure $\PageIndex{2}$: A rhombus with diagonals.

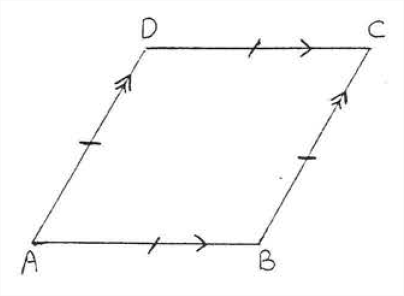
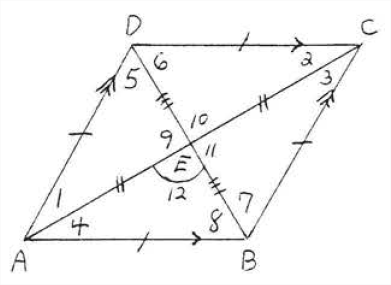
A rhombus is a parallelogram in which all sides are equal (Figure $\PageIndex{1}$). It has all the properties of a parallelogram plus some additional ones as well. Let us draw the diagonals $AC$ and $BD$ (Figure $\PageIndex{2}$). By Theorem $\PageIndex{3}$ of section 3.1 the diagonals bisect each other. Hence

\[\triangle ADE \cong \triangle CDE \cong \triangle CBE \cong \triangle ABE \nonumber\]

by $SSS = SSS$. The corresponding angles of the congruent triangles are equal:

\[\angle 1 = \angle 2 = \angle 3 = \angle 4, \nonumber\]

\[\angle 5 = \angle 6 = \angle 7 = \angle 8 \nonumber\]

and

\[\angle 9 = \angle 10 = \angle 11 = \angle 12. \nonumber\]

$\angle 9$ and $\angle 10$ are supplementary in addition to being equal, hence $\angle 9 = \angle 10 = \angle 11 = \angle 12 = 90^{\circ}$. We have proven the following theorem:

Theorem $\PageIndex{1}$

The diagonals of a rhombus are perpendicular and bisect the angles. See Figure $\PageIndex{3}$.

Figure $\PageIndex{3}$: The diagonals of a rhombus are perpendicular and bisect the angles.

Example $\PageIndex{1}$

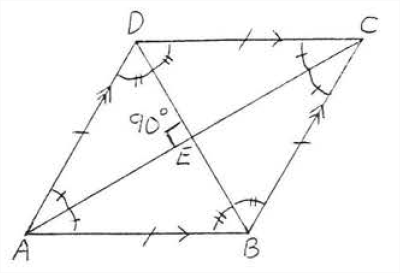
Find $w$, $x$, $y$, and $z$:

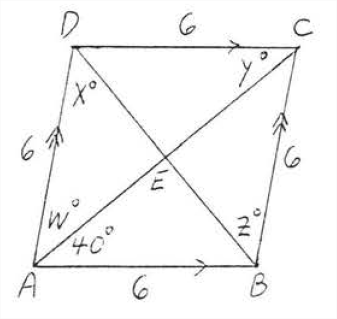
Solution

$ABCD$ is a rhombus since it is a parallelogram all of whose sides equal 6. According to Theorem $\PageIndex{1}$, the diagonals are perpendicular and bisect the angles. Therefore $w^{\circ}=40^{\circ}$ since $AC$ bisects $\angle BAD$. $\angle AED = 90^{\circ}$ so $x^{\circ} = 180^{\circ} - (90^{\circ} + 40^{\circ}) = 180^{\circ} - 130^{\circ} = 50^{\circ}$ (the sum of the angles of $\angle AED$ is $180^{\circ}$ ). Finally $y^{\circ} = w^{\circ} = 40^{\circ}$ (compare with Figure $\PageIndex{3}$) and $z^{\circ} = x^{\circ} = 50^{\circ}$.

Answer

$w = 40, x = 50, y = 40, z = 50$.

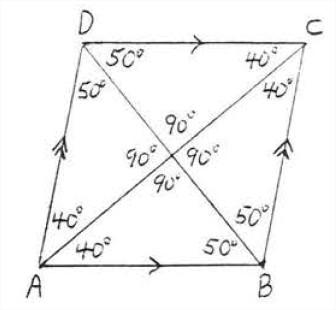
Figure $\PageIndex{4}$ shows rhombus $ABCD$ of Example $\PageIndex{1}$ with all its angles identified.

Figure $\PageIndex{4}$: The rhombus of Example $\PageIndex{1}$ with all angles identified.

A rectangle is a parallelogram in which all the angles are right angles (Figure $\PageIndex{5}$). It has all the properties of a parallelogram plus some additional ones as well. It is not actually necessary to be told that all the angles are right angles:

Figure $\PageIndex{6}$: A parallelogram with just one right angle must also be a rectangle.

Theorem $\PageIndex{2}$

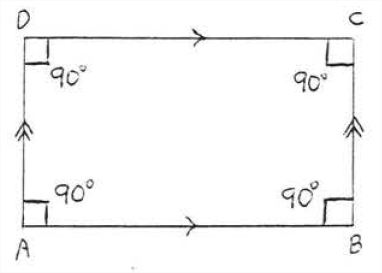
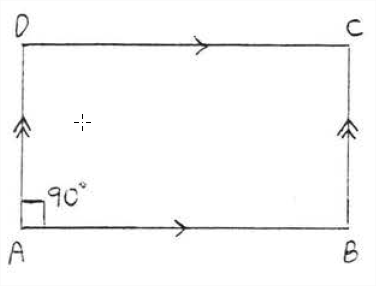
A parallelogram with just one right angle must be a rectangle.

In Figure $\PageIndex{6}$ if $\angle A$ is a right angle then all the other angles must be right angles too.

Proof: In Figure $\PageIndex{6}$, $\angle C = \angle A = 90^{\circ}$ because the opposite angles of a parallelogram are equal (Theorem $\PageIndex{1}$, section 3.1). $\angle B = 90^{\circ}$ and $\angle D = 90^{\circ}$ because the successive angles of a parallelogram are supplementary (Theorem $\PageIndex{2}$, section 3.2).

Example $\PageIndex{2}$

Find $x$ and $y$:

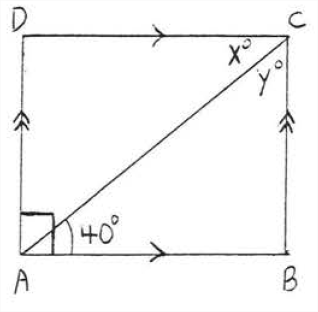
Solution

Theorem $\PageIndex{2}$, $ABCD$ is a rectangle. $x^{\circ}=40^{\circ}$ because alternate interior angles of parallel lines $AB$ and $CD$ must be equal. Since the figure is a rectangle $\angle BCD = 90^{\circ}$ and $y^{\circ} = 90^{\circ} - x^{\circ} = 90^{\circ} - 40^{\circ} = 50^{\circ}.$

Answer: $x = 40, y = 50$

Let us draw the diagonals of rectangle $ABCD$ (Figure $\PageIndex{7}$).

Figure $\PageIndex{7}$: Rectangle wIth diagonals drawn.

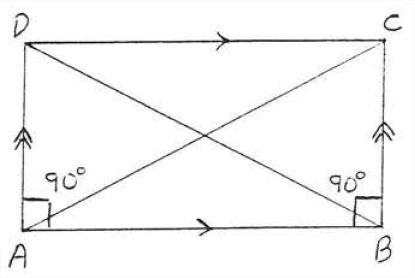
We will show $\triangle ABC \cong \triangle BAD$. $AB = BA$ because of identity. $\angle A = \angle B = 90^{\circ}$. $BC = AD$ because the opposite sides of a parallelogram are equal. Then $\triangle ABC \cong \triangle BAD$ by $SAS = SAS$. Therefore diagonal $AC =$ diagonal $B D$ because they are corresponding sides of congruent triangles. We have proven:

Theorem $\PageIndex{3}$

The diagonals of a rectangle are equal. In Figure $\PageIndex{7}$, $AC = BD$.

Example $\PageIndex{3}$

Find $w$, $x$, $y$, $z$, $AC$ and $BD$:

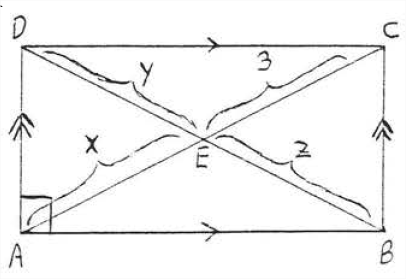
Solution

$x = 3$ because the diagonals of a parallelogram bisect each other. So $AC = 3 + 3 = 6$. $BD = AC = 6$ since the diagonals of a rectangle are equal (Theorem $\PageIndex{3}$). Therefore $y = z = 3$ since diagonal $BD$ is bisected by diagonal $AC$.

Answer: $x= y = z = 3$ and $AC = BD = 6$.

Example $\PageIndex{4}$

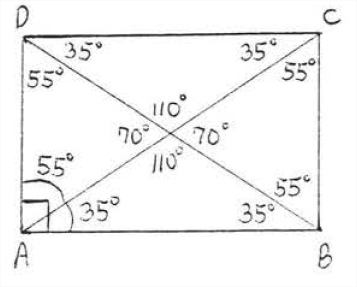
Find $x$, $y$, and $z$:

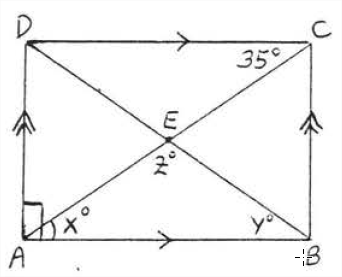
Solution

$x^{\circ} = 35^{\circ}$, because alternate interior angles of parallel lines are equal. $y^{\circ} = x^{\circ} = 35^{\circ}$ because they are base angles of isosceles triangle $ABE$ so (AE= BE\) because the diagonals of a rectangle are equal and bisect each other). $z^{\circ} = 180^{\circ} - (x^{\circ} + y^{\circ}) = 180^{\circ} - (35^{\circ} + 35^{\circ}) = 180^{\circ} - 70^{\circ} = 110^{\circ}$. Figure $\PageIndex{8}$ shows rectangle $ABCD$ with all the angles identified.

Answer: $x=y=z=3, A C=B D=6$.

Figure $\PageIndex{8}$: The rectangle of Example $\PageIndex{4}$ with all the angles identified.

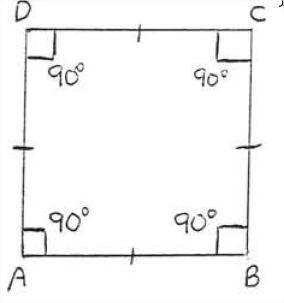
The Square

A square is a rectangle with all its sides equal. It is therefore also a rhombus. So it has all the properties of the rectangle and all the properties of the rhombus.

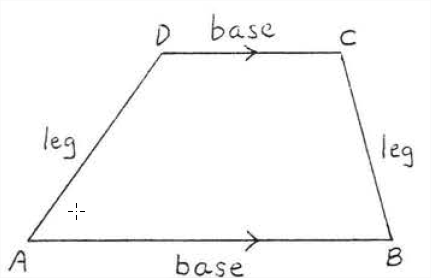
A trapezoid is a quadrilateral with two and only two sides parallel. The parallel sides are called bases and the other two sides are called legs. In Figure $\PageIndex{8}$ $AB$ and $CD$ are the bases and $AD$ and $BC$ are the legs. $\angle A$ and $\angle B$ are a pair of base angles. $\angle C$ and $\angle D$ are another pair of base angles.

An isosceles trapezoid is a trapezoid in which the legs are equal. In Figure $\PageIndex{8}$, $ABCD$ is an isosceles trapezoid with $AD = BC$. An isosceles trapezoid has the following property:

Theorem $\PageIndex{4}$

The base angles of an isosceles trapezoid are equal. In Figure $\PageIndex{11}$, $\angle A = \angle B$ and $\angle C = \angle D$

Figure $\PageIndex{11}$: An isosceles trapezoid

Example $\PageIndex{5}$

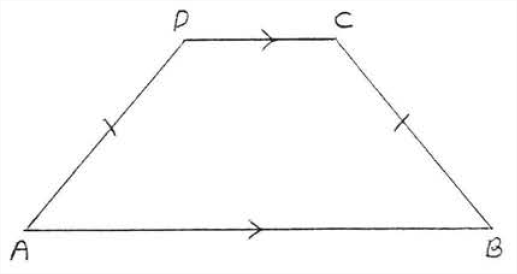
Find $x, y$, and $z:$

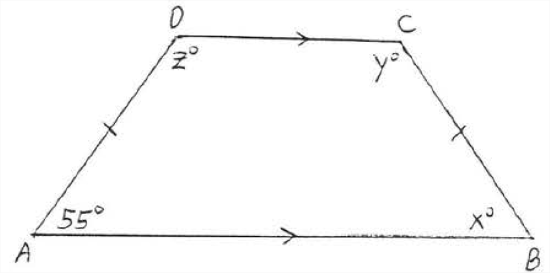
Solution

$x^{\circ}=55^{\circ}$ because $\angle A$ and $\angle B$, the base angles of isosceles trapezoid $ABCD$, are equal. Now the interior angles of parallel lines on the same side of the transversal are supplementary (Theorem 3 section 1.4). Therefore $y^{\circ} = 180^{\circ} - x^{\circ} = 180^{\circ} - 55^{\circ} = 125^{\circ}$ and $z^{\circ} = 180^{\circ} - 55^{\circ} = 125^{\circ}$.

Answer: $x = 22$, $y = z = 125$.

Proof of Theorem $\PageIndex{4}$: Draw $DE$ parallel to $CB$ as in Figure $\PageIndex{12}$. $\angle 1 = \angle B$ because corresponding angles of parallel lines are equal, $DE = BC$ because they are the opposite sides of parallelogram $BCDE$. Therefore $AD = DE$. So $\triangle ADE$ is isosceles and its base angles, $\angle A$ and $\angle 1$, are equal. We have proven $A = \angle 1 = \angle B$. To prove $\angle C = \angle D$, observe that they are both supplements of $\angle A = \angle B$ (Theorem $\PageIndex{3}$, section 1.4).

The isosceles trapezoid has one additional property:

Theorem $\PageIndex{5}$

The diagonals of an isosecles trapezoid are equal.

In Figure $\PageIndex{13}$, $AC = BD$

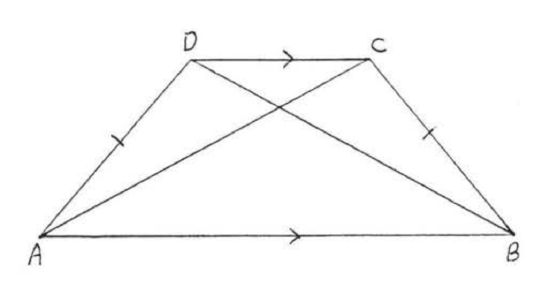
屏幕快照 2020-11-11 下午4.42.41.png — Figure $\PageIndex{13}$. The diagonals $AC$ and $BD$ are equal.

Proof: $BC = AD$, given, $\angle ABC = \angle BAD$ because they are the base angles of isosceles trapezoid $ABCD$ (Theorem $\PageIndex{4}$). $AB = BA$, identity. Therefore $\triangle ABC \cong \triangle BAD$ by $SAS = SAS$. So $AC = BD$ because they are corresponding sides of the congruent triangles.

Example $\PageIndex{6}$

Find $x$ if $AC = \dfrac{2}{x}$ and $BD = 3 - x$:

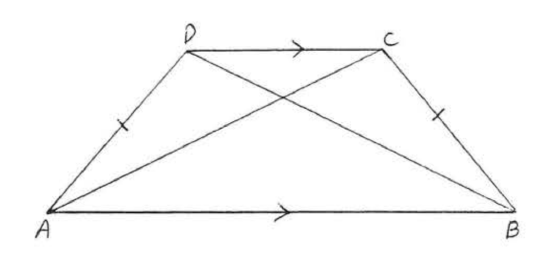
$屏幕快照 2020-11-11 下午4.46.11.png$

Solution

By Theorem $\PageIndex{5}$,

$\begin{array} {rcl} {AC} & = & {BD} \\ {\dfrac{2}{x}} & = & {3 - x} \\ {(x)\dfrac{2}{x}} & = & {(3 - x)(x)} \\ {2} & = & {3x - x^2} \\ {x^2 - 3x + 2} & = & {0} \\ {(x - 1)(x - 2)} & = & {0} \end{array}$

$\begin{array} {rcl} {x - 1} & = & {0} \\ {x} & = & {1} \end{array}$ $\begin{array} {rcl} {x - 2} & = & {0} \\ {x} & = & {2} \end{array}$

Check, $x = 1$:

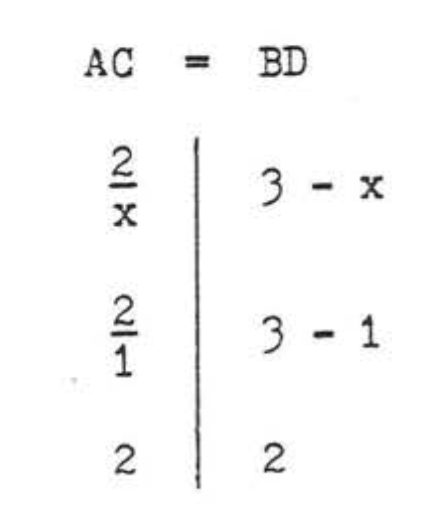
$屏幕快照 2020-11-11 下午4.54.21.png$

Check, $x = 2$:

$屏幕快照 2020-11-11 下午4.55.03.png$

Answer: $x = 1$ or $x = 2$.

SUMMARY

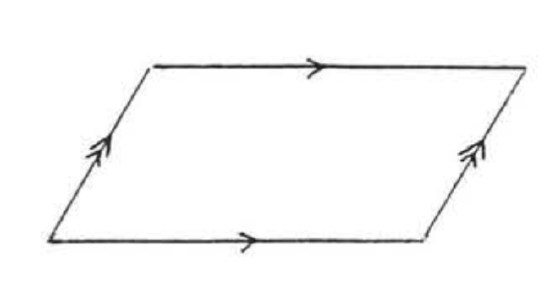
$屏幕快照 2020-11-11 下午4.56.22.png$

THE PARALLELOGRAM

A quadrilateral in which the opposite sides are parallel.

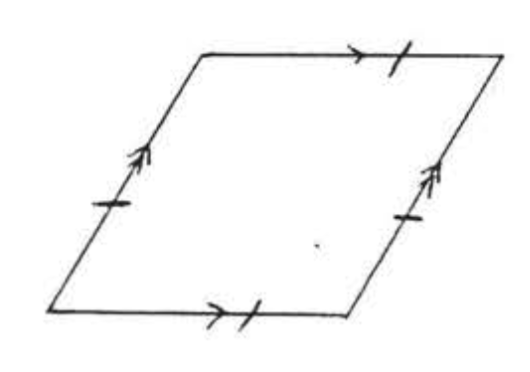
$屏幕快照 2020-11-16 下午3.13.04.png$

THE RHOMBUS

A parallelogram in which all of the sides are equal.

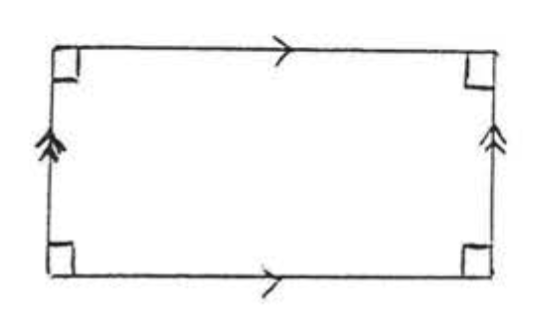
$屏幕快照 2020-11-16 下午3.15.42.png$

THE RECTANGLE

A parallelogram in which all of the angles are equal to $90^{\circ}$.

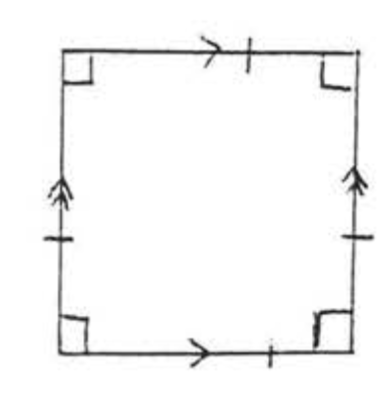
$屏幕快照 2020-11-16 下午3.16.37.png$

THE SQUARE

A parallelogram which is both a rhombus and a rectangle.

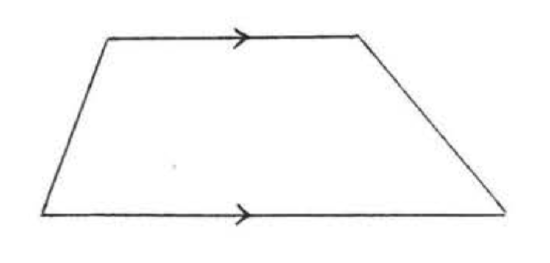
$屏幕快照 2020-11-16 下午3.23.32.png$

THE TRAPEZOID

A quadrilateral with just one pair of parallel sides.

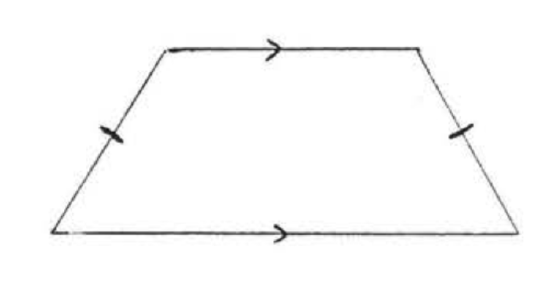
$屏幕快照 2020-11-16 下午3.24.43.png$

THE ISOSCELES TRAPEZOID

A trapezoid in which the non-parallel sides are equal.

PROPERTIES OF QUADRILATERALS

	Opposite sides are parallel	Opposite sides are equal	Opposite angles	Diagonals bisect each other	Diagonals are equal	Diagonals are perpendicular	Diagonals bisect the angles	All sides are equal	All angles are equal
Parallelogram	YES	YES	YES	YES	-	-	-	-	-
Rhombus	YES	YES	YES	YES	-	YES	YES	YES	-
Rectangle	YES	YES	YES	YES	YES	-	-	-	YES
Trapezoid	*	-	-	-	-	-	-	-	-
Isosceles Trapezoid	*	*	-	-	YES	-	-	-	-

*One pair only.

Problems

For each of the following state any theorems used in obtaining your answer.

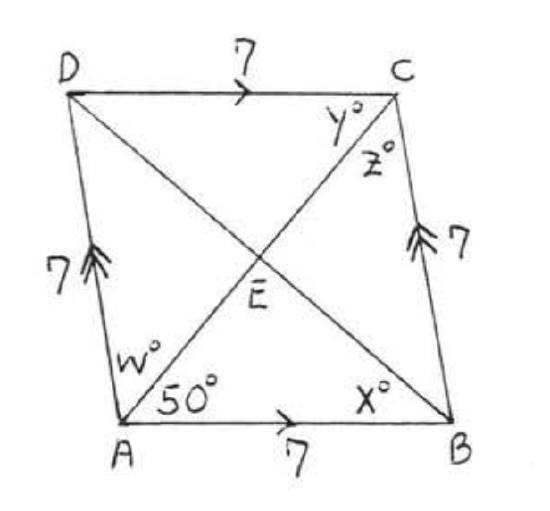
1. Find $w, x, y$, and $z$:

$Screen Shot 2020-11-16 at 3.39.32 PM.png$

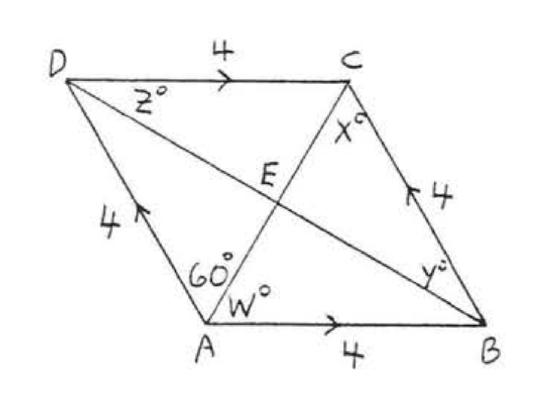
2. Find $w, x, y$, and $z$:

$Screen Shot 2020-11-16 at 3.39.53 PM.png$

3. Find $x$ and $y$:

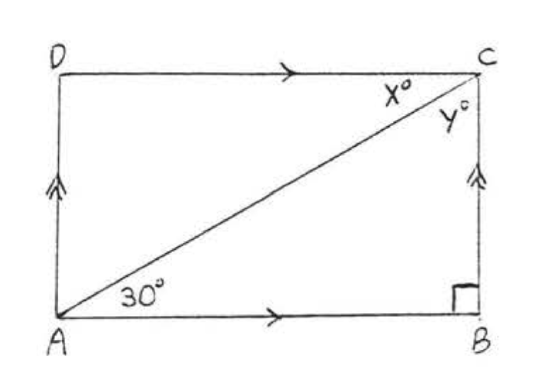
$Screen Shot 2020-11-16 at 3.40.08 PM.png$

4. Find $x$ and $y$:

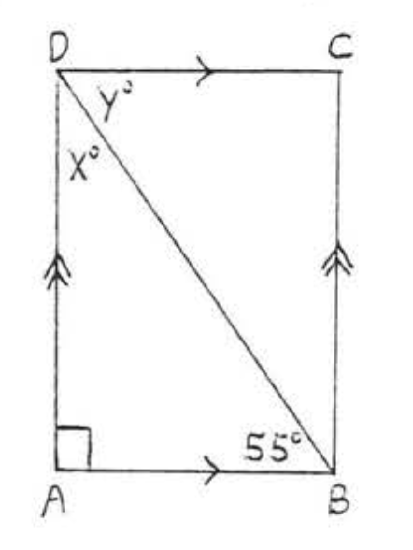
$Screen Shot 2020-11-16 at 3.40.26 PM.png$

5. Find $x, y, z, AC$ and $BD$:

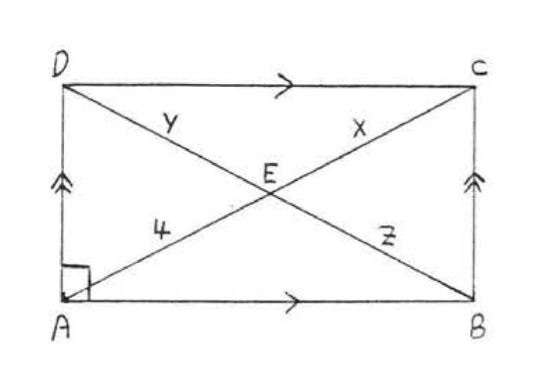
$Screen Shot 2020-11-16 at 3.40.53 PM.png$

6. Find $x, y$, and $z$:

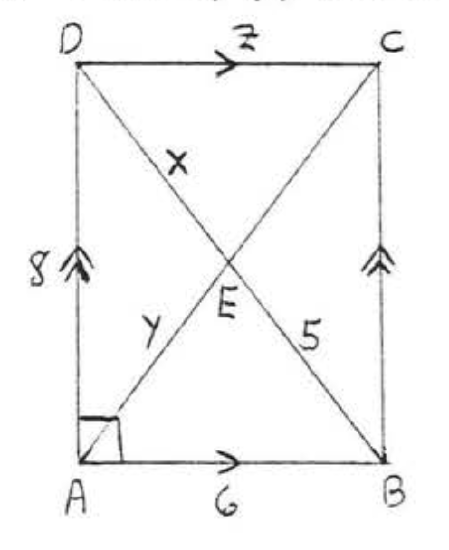
$Screen Shot 2020-11-16 at 3.42.15 PM.png$

7. Find $x, y$, and $z$:

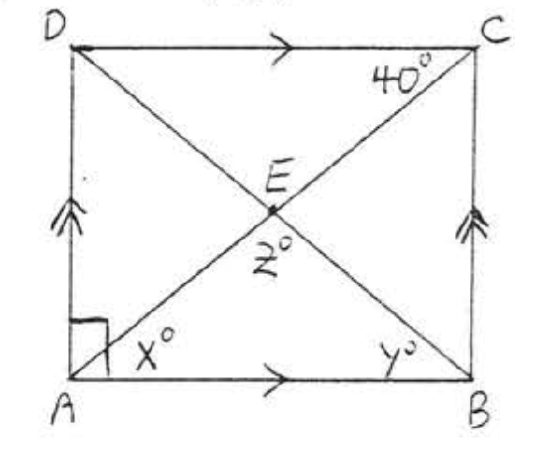
$Screen Shot 2020-11-16 at 3.41.57 PM.png$

8. Find $x, y$, and $z$:

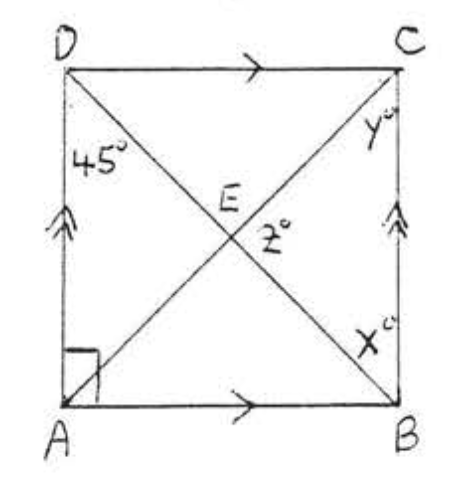
$Screen Shot 2020-11-16 at 3.42.45 PM.png$

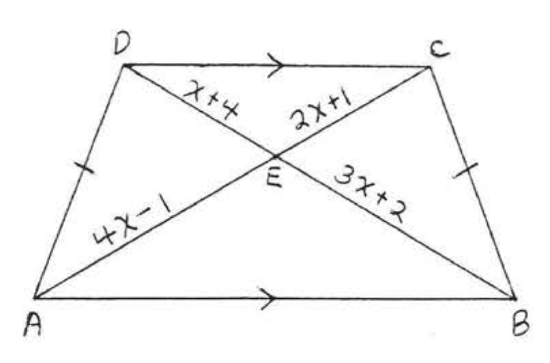
9. Find $x$ if $AC = \dfrac{3}{x}$ and $BD = 4x - 1$:

$Screen Shot 2020-11-16 at 3.43.05 PM.png$

10. Find $x$ and $y$:

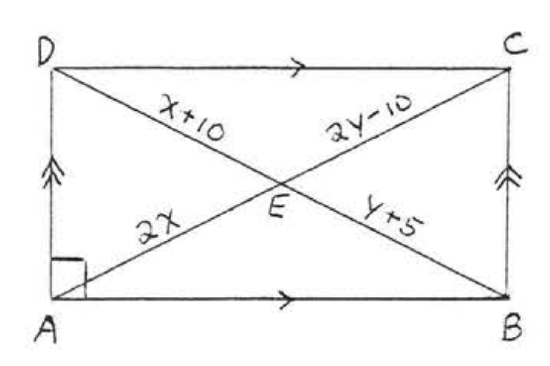
$Screen Shot 2020-11-16 at 3.43.21 PM.png$

11. Find $x, y$, and $z$:

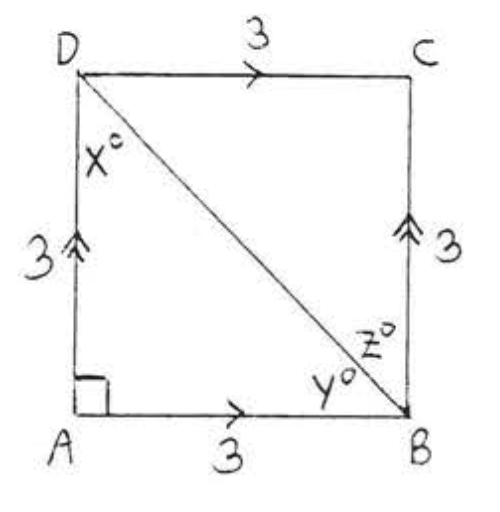
$Screen Shot 2020-11-16 at 3.43.41 PM.png$

12. Find $x, y$, and $z$:

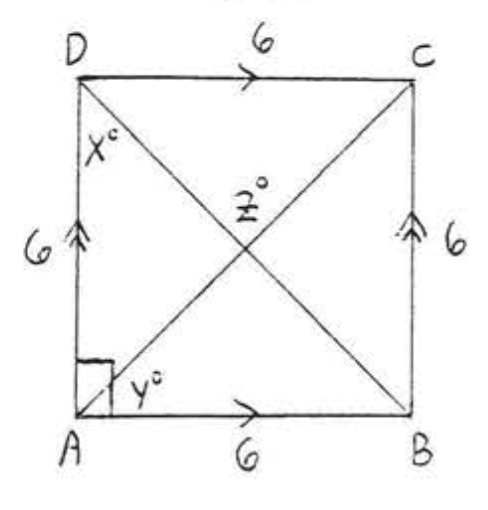
$Screen Shot 2020-11-16 at 3.44.03 PM.png$

13. Find $x, y$, and $z$:

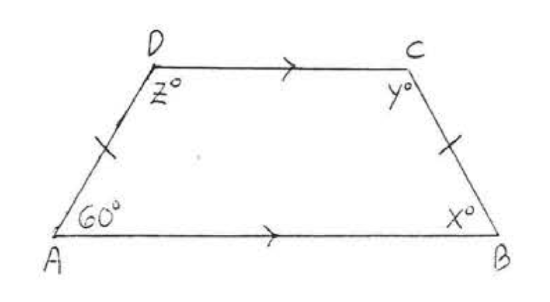
$Screen Shot 2020-11-16 at 3.44.23 PM.png$

14. Find $x, y$, and $z$:

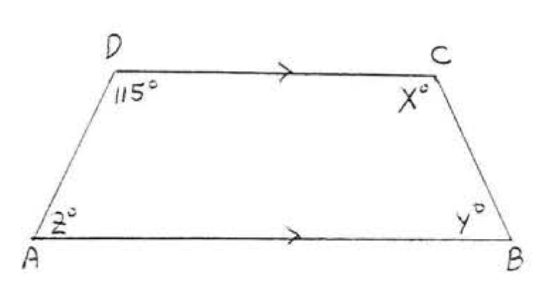
$Screen Shot 2020-11-16 at 3.44.44 PM.png$

15. Find $x$ and $y$:

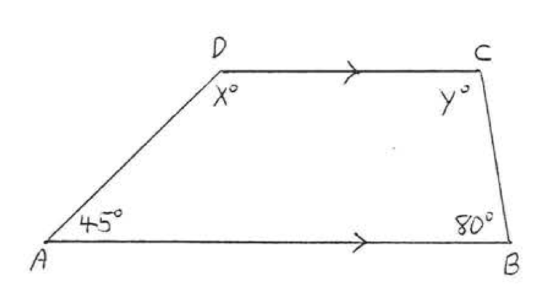
$Screen Shot 2020-11-16 at 3.45.08 PM.png$

16. Find $x, y, \angle A, \angle B, \angle C$, and $\angle D$:

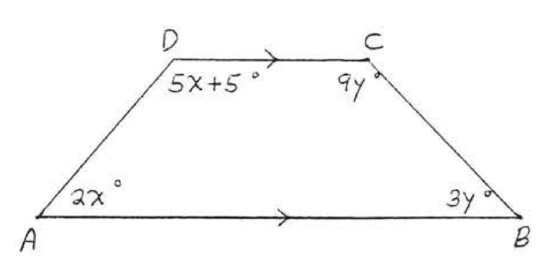
$Screen Shot 2020-11-16 at 3.45.25 PM.png$

17. Find $w, x, y$, and $z$:

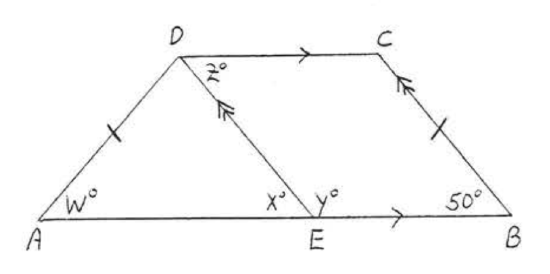
$Screen Shot 2020-11-16 at 3.45.44 PM.png$

18. Find $x, y$, and $z$:

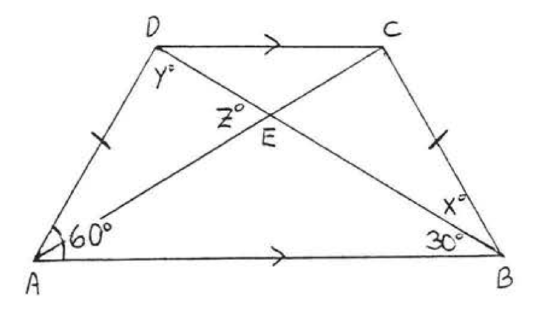
$Screen Shot 2020-11-16 at 3.46.00 PM.png$

19. Find $x$ if $AC = x^2 - 13$ and $BD = 2x + 2$:

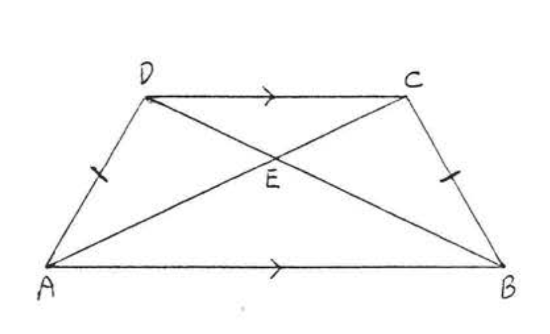
$Screen Shot 2020-11-16 at 3.46.21 PM.png$

20. Find $x$, $AC$ and $BD$:

$Screen Shot 2020-11-16 at 3.46.41 PM.png$

Search

Text Color

Text Size

Margin Size

Font Type

Theorem \(\PageIndex{4}\)

Example \(\PageIndex{5}\)

Theorem \(\PageIndex{5}\)

Example \(\PageIndex{6}\)

Theorem \(\PageIndex{1}\)

Example \(\PageIndex{1}\)

Theorem \(\PageIndex{2}\)

Example \(\PageIndex{2}\)

Theorem \(\PageIndex{3}\)

Example \(\PageIndex{3}\)

Example \(\PageIndex{4}\)

The Square

Theorem \(\PageIndex{4}\)

Example \(\PageIndex{5}\)

Theorem \(\PageIndex{5}\)

Example \(\PageIndex{6}\)

SUMMARY

PROPERTIES OF QUADRILATERALS

Problems