5.3: Uniqueness of a perpendicular
- Page ID
- 23607
There is one and only one line that passes thru a given point \(P\) and is perpendicular to a given line \(\ell\).
According to the above theorem, there is a unique point \(Q \in \ell\) such that \((QP) \perp \ell\). This point \(Q\) is called the foot point of \(P\) on \(\ell\).
- Proof
-
If \(P \in \ell\), then both existence and uniqueness follow from Axiom III.
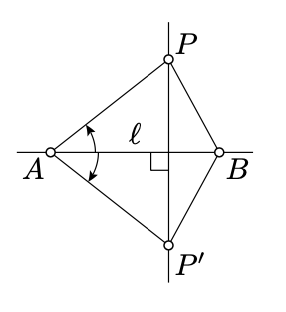
Existence for \(P \not\in \ell\). Let \(A\) and \(B\) be two distinct points of \(\ell\). Choose \(P'\) so that \(AP' = AP\) and \(\meauredangle BAP' \equiv - \measuredangle BAP\). According to Axiom IV, \(\triangle AP'B \cong \triangle APB\). In particular, \(AP = AP'\) and \(BP = BP'\).
According to Theorem 5.2.1, \(A\) and \(B\) lie on the perpendicular bisector to \([PP']\). In particular, \((PP') \perp (AB) = \ell\).
Uniqueness for \(P \not\in \ell\). From above we can choose a point \(P'\) in such a way that \(\ell\) forms the perpendicular bisector to \([PP']\).
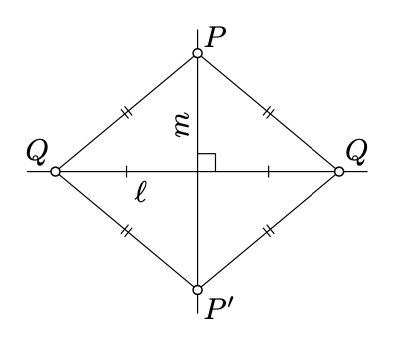
Assume \(m \perp \ell\) and \(P \in m\). Then \(m\) is a perpendicular bisector to some segment \([QQ']\) of \(\ell\); in particular, \(PQ = PQ'\).
Since \(\ell\) is the perpendicular bisector to \([PP']\), we get that \(PQ = P'Q\) and \(PQ' = P'Q'\). Therefore,
\(P'Q = PQ = PQ' = P'Q'\).
By Theorem 5.2.1, \(P'\) lies on the perpendicular bisector to \([QQ']\), which is \(m\). By Axiom II, \(m = (PP')\).


