5.4: Reflection across a line

Assume the point \(P\) and the line \((AB)\) are given. To find the reflection \(P'\) of \(P\) across \((AB)\), one drops a perpendicular from \(P\) onto \((AB)\), and continues it to the same distance on the other side.

According to Theorem 5.3.1, \(P'\) is uniquely determined by \(P\).
Note that \(P = P'\) if and only if \(P \in (AB)\).

Proposition \(\PageIndex{1}\)

Assume \(P'\) is a reflection of the point \(P\) across \((AB)\). Then \(AP' = AP\) and if \(A \ne P\), then \(\measuredangle BAP' \equiv -\measuredangle BAP\).

Proof

Note that if \(P \in (AB)\), then \(P = P'\). By Corollary 2.4.1, \(\measuredangle BAP = 0\) or \(\pi\). Hence the statement follows.

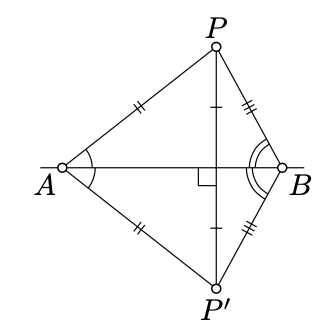
If \(P \not\in (AB)\), then \(P' \ne P\). By the construction of \(P'\), the line \((AB)\) is a perpendicular bisector of \([PP']\). Therefore, according to Theorem 5.3.1, \(AP' = AP\) and \(BP' = BP\). In particular, \(\triangle ABP' \cong \triangle ABP\). Therefore, \(\measuredangle BAP' = \pm \measuredangle BAP\).

Since \(P' \ne P\) and \(AP' = AP\), we get that \(\measuredangle BAP' \ne \measuredangle BAP\). That is, we are let with the case

\(\measuredangle BAP' = -\measuredangle BAP.\)

Corollary \(\PageIndex{1}\)

The reflection across a line is a motion of the plane. Moreover, if \(\triangle P'Q'R'\) is the reflection of \(\triangle PQR\), then

\(\measuredangle Q'P'R' \equiv \measuredangle QPR.\)

Proof

Note that the composition of two reflections across the same line is the identity map. In particular, any reflection is a bijection.

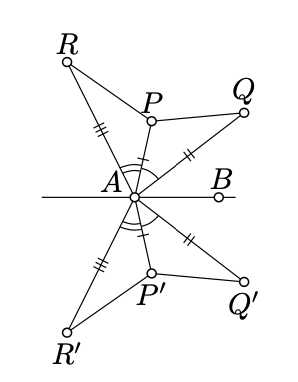
Fix a line \((AB)\) and two points \(P\) and \(Q\); denote their reflections across \((AB)\) by \(P'\) and \(Q'\). Let us show that

\[P'Q' = PQ;\]

that is, the reflection is distance-preserving, Without loss of generality, we may assume that the points \(P\) and \(Q\) are distinct from \(A\) and \(B\). By Proposition \(\PageIndex{1}\), we get that

\(\begin{array} {rcl} {\measuredangle BAP'} & \equiv & {-\measuredangle BAP,} \\ {AP'} & = & {AP,} \end{array}\) \(\begin{array} {rcl} {\measuredangle BAQ'} & \equiv & {-\measuredangle BAQ,} \\ {AQ'} & = & {AQ.} \end{array}\)

It follows that

\[\measuredangle P'AQ' \equiv - \measuredangle PAQ.\]

By SAS, \(\triangle P'AQ' \cong \triangle PAQ\) and 5.4.1 follows. Moreover, we also get that

\(\measuredangle AP'Q' \equiv \pm \measuredangle APQ.\)

From 5.4.2 and the theorem on the signs of angles of triangles (Theorem 3.3.1) we get

\[\measuredangle AP'Q' \equiv - \measuredangle APQ.\]

Repeating the same argument for a pair of points \(P\) and \(R\), we get that

\[\measuredangle AP'R' \equiv -\measuredangle APR.\]

Subtracting 5.4.4 from 5.4.3, we get that

\(\measuredangle Q'P'R' \equiv -\measuredangle QPR.\)

Exercise \(\PageIndex{1}\)

Show that any motion of the plane can be presented as a composition of at most three reflections across lines.

Hint

Choose an arbitrary nondegenerate triangle \(ABC\). Suppose that \(\triangle \hat{A} \hat{B} \hat{C}\) denotes its image after the motion.

If \(A \ne \hat{A}\), apply the reflection across the perpendicular bisector of \([A\hat{A}]\). This reflection sends \(A\) to \(\hat{A}\). Let \(B'\) and \(C'\) denote the reflections of \(B\) and \(C\) respectively.

If \(B \ne \hat{B}\), apply the reflection across the perpendicular bisector of \([B'\hat{B}]\). This reflection sends \(B'\) to \(\hat{B}\). Note that \(\hat{A} \hat{B} = \hat{A} B'\); that is, \(\hat{A}\) lies on the perpendicular bisector. Therefore, \(\hat{A}\) reflects to itself. Suppose that \(C''\) denotes the reflection of \(C'\).

Finally, if \(C'' \ne \hat{C}\), apply the reflection across \((\hat{A}\hat{B})\). Note that \(\hat{A}\hat{C} = \hat{A} C''\) and \(\hat{B}\hat{C} = \hat{B} C''\); that is, \((AB)\) is the perpendicular bisector of \([C''\hat{C}]\). Therefore, this reflection sends \(C''\) to \(\hat{C}\).

Apply Exercise 4.4.3 to show that the composition of the constructed reflections coincides with the given motion.

The motions of plan can be divided into two types, direct and indirect. The motion \(f\) is direct if

\(\measuredangle Q'P'R' = \measuredangle QPR\)

for any \(\triangle PQR\) and \(P' = f(P)\), \(Q' = f(Q)\) and \(R' = f(R)\); if instead we have

\(\measuredangle Q'P'R' \equiv -\measuredangle QPR\)

for any \(\triangle PQR\), then the motion \(f\) is called indirect.

Indeed, by Corollary \(\PageIndex{1}\), any reflection is an indirect motion. Applying the exercise above, any motion is a composition of reflections. If the number of reflections is odd then the composition indirect; if the number is even, then the motion is direct.

Exercise \(\PageIndex{2}\)

Let \(X\) and \(Y\) be the reflections of \(P\) across the lines \((AB)\) and \((BC)\) respectively. Show that

\(\measuredangle XBY \equiv 2 \cdot \measuredangle ABC.\)

Answer

Note that \(\measuredangle XBA = \measuredangle ABP, \measuredangle PBC = \measuredangle CBY\). Therefore,

\(\measuredangle XBY \equiv \measuredangle XBP + \measuredangle PBY \equiv 2 \cdot (\measuredangle ABP + \measuredangle PBC) \equiv 2 \cdot \measuredangle ABC.\)