5.2: Perpendicular Bisector

Assume $M$ is the midpoint of the segment $[AB]$; that is, $M \in (AB)$ and $AM = MB$.

The line $\ell$ that passes thru $M$ and perpendicular to $(AB)$, is called the perpendicular bisector to the segment $[AB]$.

Theorem $\PageIndex{1}$

Given distinct points $A$ and $B$, all points equidistant from $A$ and $B$ and no others lie on the perpendicular bisector to $[AB]$.

Proof

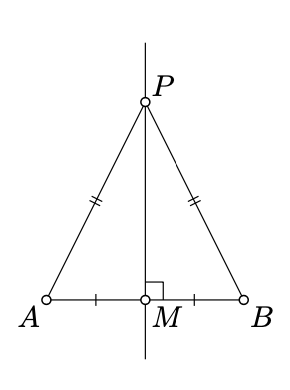
Let $M$ be the midpoint of $[AB]$.

Assume $PA = PB$ and $P \ne M$. According to SSS (Theorem 4.4.1), $\triangle AMP \cong \triangle BMP$. Hence

$\measuredangle AMP = \pm \measuredangle BMP.$

Since $A \ne B$, we have "-" in the above formula. Further,

$$\begin{array} {rcl} {\pi} & = & {\measuredangle AMB \equiv} \\ {} & \equiv & {\measuredangle AMP + \measuredangle PMB \equiv} \\ {} & \equiv & {2 \cdot \measuredangle AMP.} \end{array}$$

That is, $\measuredangle AMP = \pm \dfrac{\pi}{2}$. Therefore, $P$ lies on the perpendicular bisector.

To prove the converse, suppose $P$ is any point on the perpendicular bisector to $[AB]$ and $P \ne M$. Then $\measuredangle AMP = \pm \dfrac{\pi}{2}$, $\measuredangle BMP = \pm \dfrac{\pi}{2}$ and $AM = BM$. By SAS, $\triangle AMP \cong \triangle BMP$; in particular, $AP = BP$.

Exercise $\PageIndex{1}$

Let $\ell$ be the perpendicular bisector to the segment $[AB]$ and $X$ be an arbitrary point on the plane.

Show that $AX < BX$ if and only if $X$ and $A$ lie on the same side from $\ell$.

Hint

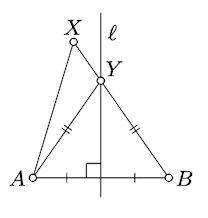
Assume $X$ and $A$ lie on the same side of $\ell$.

Note that $A$ and $B$ lie on opposite side of $\ell$. Therefore, by Corollary 3.4.1, $[AX]$ does not intersect $\ell$ and $[BX]$ intersects $\ell$; suppose that $Y$ denotes the intersection point.

Note that $BX = AY + YX \ge AX$. Since $X \not\in \ell$, by Theorem $\PageIndex{1}$ we have $BX \ne BA$. Therefore $BX > AX$.

This way we proved the "if" part. To prove the "only if" part, you need to switch $A$ and $B$ and repeat the above argument.

Exercise $\PageIndex{2}$

Let $ABC$ be a nondegenerate triangle. Show that

$AC > BC \Leftrightarrow |\measuredangle ABC| > |\measuredangle CAB|.$

Hint

Apply Exercise $\PageIndex{1}$, Theorem 4.2.1 and Exercise 3.1.2.