5.6: Circles

Recall that a circle with radius \(r\) and center \(O\) is the set of all points on distance \(r\) from \(O\). We say that a point \(P\) lies inside of the circle if \(OP < r\); if \(OP > r\), we say that \(P\) lies outside of the circle.

Exercise \(\PageIndex{1}\)

Let \(\Gamma\) be a circle and \(P \not\in \Gamma\). Assume a line \(\ell\) is passing thru the point \(P\) and intersects \(\Gamma\) at two distinct points, \(X\) and \(Y\). Show that \(P\) is inside \(\Gamma\) if and only if \(P\) lies between \(X\) and \(Y\).

Hint

Let \(O\) be the center of the circle. Note that we can assume that \(O \ne P\).

Assume \(P\) lies between \(X\) and \(Y\). By Exercise 5.1.1, we can assume that \(OPX\) is right or obtuse. By Exercise 5.5.1, \(OP < OX\); that is, \(P\) lies inside \(\Gamma\).

If \(P\) does not lie between \(X\) and \(Y\), we can assume that \(X\) lies between \(P\) and \(Y\). Since \(OX = OY\), Exercise 5.5.1 implies that \(\angle OXY\) is acute. Therefore, \(\angle OXP\) is obtuse. Applying Exercise 5.5.1 again we get that \(OP > OX\)l that is, \(P\) lies outside \(\Gamma\).

A segment between two points on a circle is called a chord of the circle. A chord passing thru the center of the circle is called its diameter.

Exercise \(\PageIndex{2}\)

Assume two distinct circles \(\Gamma\) and \(\Gamma'\) have a common chord \([AB]\). Show that the line between centers of \(\Gamma\) and \(\Gamma'\) forms a perpendicular bisector to \([AB]\).

Hint

Apply Theorem 5.2.1.

Lemma \(\PageIndex{1}\)

A line and a circle can have at most two points of intersection.

Proof

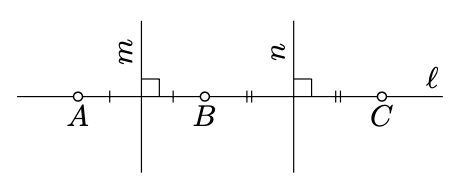
Assume \(A, B\), and \(C\) are distinct points that lie on a line \(\ell\) and a circle \(\Gamma\) with the center \(O\). Then \(OA = OB = OC\); in particular, \(O\) lies on the perpendicular bisectors \(m\) and \(n\) to \([AB]\) and \([BC]\) respectively. Note that the midpoints of \([AB]\) and \([BC]\) are distinct. Therefore, \(m\) and \(n\) are distinct. The contradicts the uniqueness of the perpendicular (Theorem 5.3.1).

Exercise \(\PageIndex{3}\)

Show that two distinct circles can have at most two points of intersection.

Hint

Use Exercise \(\PageIndex{2}\) and Theorem 5.3.1.

In consequence of the above lemma, a line \(\ell\) and a circle \(\Gamma\) might have 2, 1 or 0 points of intersections. In the first case the line is called secant line, in the second case it is tangent line; if \(P\) is the only point of intersection of \(\ell\) and \(\Gamma\), we say that \(\ell\) is tangent to \(\Gamma\) at \(P\).

Similarly, according Exercise \(\PageIndex{3}\), two distinct circles might have 2, 1 or 0 points of intersections. If \(P\) is the only point of intersection of circles \(\Gamma\) and \(\Gamma'\), we say that \(\Gamma\) is tangent to \(\Gamma\) at \(P\); we also assume that circle is tangent to it self at any of its points.

Lemma \(\PageIndex{2}\)

Let \(\ell\) be a line and \(\Gamma\) be a circle with the center \(O\). Assume \(P\) is a common point of \(\ell\) and \(\Gamma\). Then \(\ell\) is tangent to \(\Gamma\) at \(P\) if and only if \((PQ) \perp \ell\).

Proof

Let \(Q\) be the foot point of \(O\) on \(\ell\).

Assume \(P \ne Q\). Let \(P'\) be the reflection of \(P\) across \((OQ)\). Note that \(P' \in \ell\) and \((OQ)\) is the perpendicular bisector of \([PP']\). Therefore, \(OP = OP'\). Hence \(P, P' \in \Gamma \cap \ell\); that is, \(\ell\) is secant to \(\Gamma\).

If \(P = Q\), then according to Lemma 5.5.1, \(OP < OX\) for any point \(X \in \ell\) distinct from \(P\). Hence \(P\) is the only point in the intersection \(\Gamma \cap \ell\); that is, \(\ell\) is tangent to \(\Gamma\) at \(P\).

Exercise \(\PageIndex{4}\)

Let \(\Gamma\) and \(\Gamma'\) be two distinct circles with centers at \(O\) and \(O'\) respectively. Assume \(\Gamma\) meets \(\Gamma'\) at point \(P\). Show that \(\Gamma\) is tangent to \(\Gamma'\) if and only if \(O\), \(O'\), and \(P\) lie on one line.

Hint

Let \(P'\) be the reflection of \(P\) across \((OO')\). Note that \(P'\) lies on both circles and \(P' \ne P\) if and only if \(P \not\in (OO')\).

Exercise \(\PageIndex{5}\)

Let \(\Gamma\) and \(\Gamma'\) be two distinct circles with centers at \(O\) and \(O'\) and radiuses \(r\) and \(r'\). Show that \(\Gamma\) is tangent to \(\Gamma'\) if and only if

\(OO' = r + r'\) or \(OO' = |r - r'|\).

Hint

Apply Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{6}\)

Assume three circles have two points in common. Prove that their centers lie on one line.

Hint

Let \(A\) and \(B\) be the points of intersection. Note that the centers lie on the perpendicular bisector of the segment \([AB]\).