8.5: Equidistant Property
( \newcommand{\kernel}{\mathrm{null}\,}\)
Recall that distance from a line
Assume
- Proof
-
We can assume that
Let
Otherwise both lines
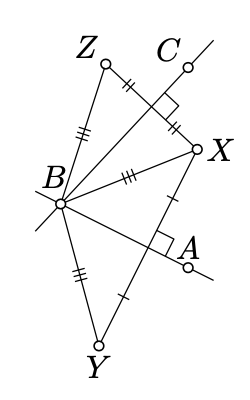
Note that
Since
By Proposition 5.4.1,
By 8.5.1,
The last identity means either
and hence the result.


