10.6: Angles after inversion
- Page ID
- 23645
In the inversive plane, the inverse of an arc is an arc.
- Proof
-
Consider four distinct points \(A, B, C\), and \(D\); let \(A', B', C'\), and \(D'\) be their inverses. We need to show that \(D\) lies on the arc \(ABC\) if and only if \(D'\) lies on the arc \(A'B'C'\). According to Proposition 9.5.1, the latter is equivalent to the following:
\(\measuredangle ADC = \measuredangle ABC \Leftrightarrow \measuredangle A'D'C' = \measuredangle A'B'C'.\)
The latter follows from Theorem 10.2.1b.
The following theorem states that the angle between arcs changes only its sign after the inversion.
Let \(AB_1C_1\), \(AB_2C_2\) be two arcs in the inversive plane, and the arcs \(A'B_1'C_1'\), \(A'B_2'C_2'\) be their inverses. Let \([AX_1)\) and \([AX_2)\) be the half-lines tangent to \(AB_1C_1\) and \(AB_2C_2\) at \(A\), and \([A'Y_1)\) and \([A'Y_2)\) be the half-lines tangent to \(A'B_1'C_1'\) and \(A'B_2'C_2'\) at \(A'\). Then
\(\measuredangle X_1AX_2 \equiv -\measuredangle Y_1A'Y_2\).
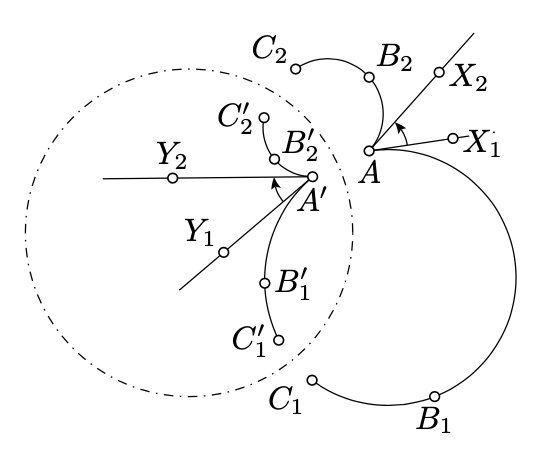
- Proof
-
Applying to Proposition 9.6.1,
\(\begin{array} {rcl} {\measuredangle X_1AX_2} & \equiv & {\measuredangle X_1AC_1 + \measuredangle C_1AC_2 + \measuredangle C_2AX_2 \equiv} \\ {} & \equiv & {(\pi - \measuredangle C_1B_1A) + \measuredangle C_1AC_2 + (\pi - \measuredangle AB_2C_2) \equiv} \\ {} & \equiv & {-(\measuredangle C_1B_1A + \measuredangle AB_2C_2 + \measuredangle C_2AC_1) \equiv} \\ {} & \equiv & {-(\measuredangle C_1B_1A + \measuredangle AB_2C_1) -(\measuredangle C_1B_2C_2 + \measuredangle C_2AC_1).} \end{array}\)
The same way we get that
\(\measuredangle Y_1A'Y_2 \equiv -(\measuredangle C_1'B_1'A' + \measuredangle A'B_2'C_1') - (\measuredangle C_1'B_2'C_2' + \measuredangle C_2'A'C_1').\)
By Theorem 10.2.1b,
\(\begin{array} {rcl} {\measuredangle C_1B_1A + \measuredangle AB_2C_1} & \equiv & {-(\measuredangle C_1'B_1'A' + \measuredangle A'B_2'C_1'),} \\ {\measuredangle C_1B_2C_2 + \measuredangle C_2AC_1} & \equiv & {-(\measuredangle C_1'B_2'C_2' + \measuredangle C_2'A'C_1')} \end{array}\).
and hence the result.
The angle between arcs can be defined as the angle between its tangent half-lines at the common endpoint. Therefore under inversion, the angles between arcs are preserved up to sign.
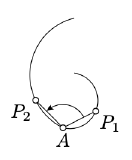
From Exercise 5.7.4, it follows that the angle between arcs with common endpoint A is the limit of \(\measuredangle P_1AP_2\) where \(P_1\) and \(P_2\) are points approaching \(A\) along the corresponding arcs. This observation can be used to define the angle between a pair of curves emerging from one point. It turns out that under inversion, angles between curves are also preserved up to sign.
Let \(P\) be the inverse of point \(Q\) in a circle \(\Gamma\). Assume that \(P'\), \(Q'\), and \(\Gamma'\) are the inverses of \(P, Q\), and \(\Gamma\) in another circle \(\Omega\). Then \(P'\) is the inverse of \(Q'\) in \(\Gamma'\).
- Proof
-
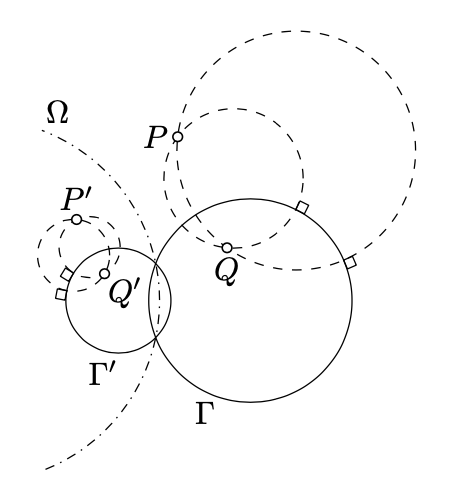
If \(P = Q\), then \(P'=Q' \in \Gamma'\). Therefore, \(P'\) is the inverse of \(Q'\) in \(\Gamma'\).
It remains to consider the case \(P \ne Q\). Let \(\Delta_2\) and \(\Delta_2\) be two distinct circles that intersect at \(P\) and \(Q\). According to Corollary 10.5.2, \(\Delta_1 \perp \Gamma\) and \(\Delta_2 \perp \Gamma\).
Let \(\Delta_1'\) and \(\Delta_2'\) denote the inverses of \(\Delta_1\) and \(\Delta_2\) in \(Omega\). Clearly, \(\Delta_1'\) meets \(\Delta_2'\) at \(P'\) and \(Q'\).
By Theorem \(\PageIndex{1}\), \(\Delta_1' \perp \Gamma'\) and \(\Delta_2' \perp \Gamma'\). By Corollary 10.5.1, \(P'\) is the inverse of \(Q'\) in \(\Gamma'\).


