9.6: Tangent half-lines
- Page ID
- 23638
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Suppose \(ABC\) is an arc of a circle \(\Gamma\). A half-line \([AX)\) is called tangent to the arc \(ABC\) at \(A\) if the line \((AX)\) is tangent to \(\Gamma\), and the points \(X\) and \(B\) lie on the same side of the line \((AC)\).
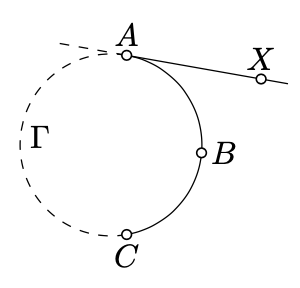
If the arc is formed by the line segment \([AC]\) then the half-line \([AC)\) is considered to be tangent at \(A\). If the arc is formed by a union of two half lines \([AX)\) and \([BY)\) in \((AC)\), then the half-line \([AX)\) is considered to be tangent to the arc at \(A\).
The half-line \([AX)\) is tangent to the arc \(ABC\) if and only if
\(\measuredangle ABC + \measuredangle CAX \equiv \pi\).
- Proof
-
For a degenerate arc \(ABC\), the statement is evident. Further we assume the arc \(ABC\) is nondegenerate.
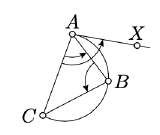
Applying Theorem 9.1.1 and Theorem 9.2.1, we get that
\(2 \cdot \measuredangle ABC + 2 \cdot \measuredangle CAX \equiv 0\).
Therefore, either
\(\measuredangle ABC + \measuredangle CAX \equiv \pi\), or \(\measuredangle ABC + \measuredangle CAX \equiv 0\).
Since \([AX)\) is the tangent half-line to the arc \(ABC, X\) and \(B\) lie on the same side of \((AC)\). By Corollary 3.4.1 and Theorem 3.3.1, the angles \(CAX\), \(CAB\), and \(ABC\) have the same sign. In particular, \(\measuredangle ABC + \measuredangle CAX \not\equiv 0\); that is, we are left with the case
\(\measuredangle ABC +\measuredangle CAX \equiv \pi\).
Show that there is a unique arc with endpoints at the given points \(A\) and \(C\), that is tangent to the given half line \([AX)\) at \(A\).
- Hint
-
If \(C \in (AX)\), then the arc is the line segment \([AC]\) or the union of two half-lines in \((AX)\) with vertices at \(A\) and \(C\).
Assume \(C \not\in (AX)\). Let \(\ell\) be the perpendicular line dropped from \(A\) to \((AX)\) and \(m\) be the perpendicular bisector of \([AC]\).
Note that \(\ell \nparallel m\); set \(O = \ell \cap m\). Note that the circle with center \(O\) passing thru \(A\) is also passing thru \(C\) and tangent to \((AX)\).
Note that one the two arcs with endpoints \(A\) and \(C\) is tangent to \([AX)\).
The uniqueness follow from Proposition \(\PageIndex{1}\).
Let \([AX)\) be the tangent half-line to an arc \(ABC\). Assume \(Y\) is a point on the arc \(ABC\) that is distinct from \(A\). Show that \(\measuredangle XAY \to 0\) as \(AY \to 0\).
- Hint
-
Use Proposition \(\PageIndex{1}\) and Theorem 7.4.1 to show that \(\measuredangle XAY = \measuredangle ACY\). By Axiom IIIc, \(\measuredangle ACY \to 0\) as \(AY \to 0\); hence the result.
Given two circle arcs \(AB_1C\) and \(AB_2C\), let \([AX_1)\) and \([AX_2)\) at \(A\), and \([CY_1)\) and \([CY_2)\) be the half-lines tangent to the arcs \(AB_1C\) and \(AB_2C\) at \(C\). Show that
\(\measuredangle X_1AX_2 \equiv -\measuredangle Y_1CY_2.\)
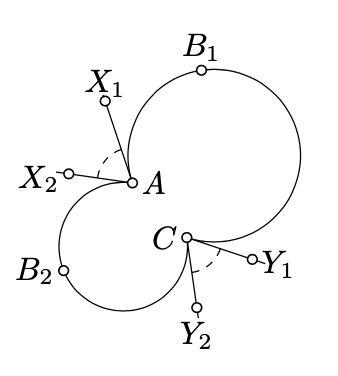
- Hint
-
Apply Proposition \(\PageIndex{1}\) twice.
(Alternatively, apply Corollary 5.4.1 for the reflection across the perpendicular bisector of \([AC]\).)