9.2: Inscribed angle

We say that a triangle is inscribed in the circle $\Gamma$ if all its vertices lie on $\Gamma$.

Theorem $\PageIndex{1}$

Let $\Gamma$ be a circle with the center $O$, and $X, Y$ be two distinct points on $\Gamma$. Then $\triangle XPY$ is inscribed in $\Gamma$ if and only if

$$2 \cdot \measuredangle XPY \equiv \measuredangle XOY.$$

Equivalently, if and only if

$\measuredangle XPY \equiv \dfrac{1}{2} \cdot \measuredangle XOY$ or $\measuredangle XPY \equiv \pi + \dfrac{1}{2} \cdot \measuredangle XOY.$

Proof

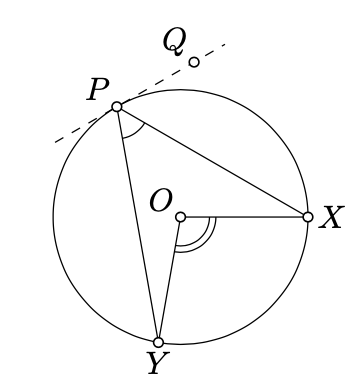
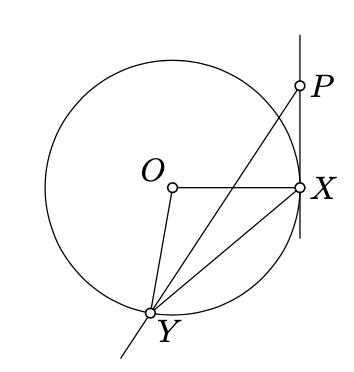
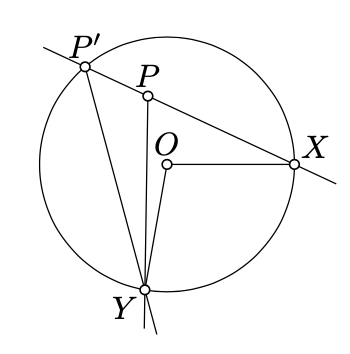
the "only if" part. Let $(PQ)$ be the tangent line to $\Gamma$ at $P$. By Theorem 9.1.1,

$2 \cdot \measuredangle QPX \equiv \measuredangle POX$, $2 \cdot \measuredangle QPY \equiv \measuredangle POY.$

Subtracting one identity from the other, we get 9.2.1.

"If" part. Assume that 9.2.1 holds for some $P \not\in \Gamma$. Note that $\measuredangle XOY \ne 0$. Therefore, $\measuredangle XPY \ne 0$ nor $\pi$; that is, $\measuredangle PXY$ is nondegenerate.

The line $(PX)$ might be tangent to $\Gamma$ at the point $X$ or intersect $\Gamma$ at another point; in the latter case, suppose that $P'$ denotes this point of intersection.

In the first case, by Theorem 9.1, we have

$2 \cdot \measuredangle PXY \equiv \measuredangle XOY \equiv 2 \cdot \measuredangle XPY.$

Applying the transversal property (Theorem 7.3.1), we get that $(XY) \parallel (PY)$, which is impossible since $\triangle PXY$ is nondegenerate.

In the second case, applying the "if" part and that $P, X$, and $P'$ lie on one line (see Exercise 2.4.2) we get that

$\begin{array} {rcl} {2 \cdot \measuredangle P'PY} & \equiv & {2 \cdot \measuredangle XPY \equiv \measuredangle XOY \equiv} \\ {} & \equiv & {2 \cdot \measuredangle XP'Y \equiv 2 \cdot \measuredangle XP'P.} \end{array}$

Again, by transversal property, $(PY) \parallel (P'Y)$, which is impossible since $\triangle PXY$ is nondegenerate.

Exercise $\PageIndex{1}$

Let $X, X', Y$, and $Y'$ be distinct points on the circle $\Gamma$. Assume $(XX')$ meets $(YY')$ at a point $P$. Show that

(a) $2 \cdot \measuredangle XPY \equiv \measuredangle XOY + \measuredangle X'OY'$;

(b) $\triangle PXY \sim \triangle PY'X'$;

(c) $PX \cdot PX' = |OP^2 - r^2|$, where $O$ is the center and $r$ is the radius of $\Gamma$.

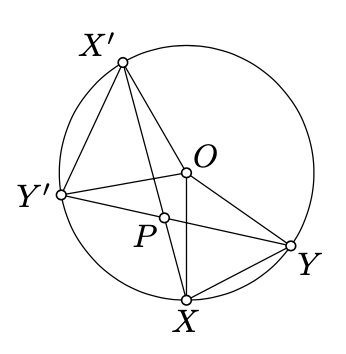
(The value $OP^2 - r^2$ is called the power of the point $P$ with respect to the circle $\Gamma$. Part (c) of the exercise makes it a useful tool to study circles, but we are not going to consider it further in the book.)

Hint

(a) Apply Theorem $\PageIndex{1}$ for $\angle XX'Y$ and $\angle X'YY'$ and Theorem 7.4.1 for $\triangle PYX'$.

(b) If $P$ is inside of $\Gamma$ then $P$ lies between $X$ and $X'$ and between $Y$ and $Y'$ in this case $\angle XPY$ is vertical to $\angle X'PY'$. If $P$ is outside of $\Gamma$ then $[PX) = [PX')$ and $[PY) = [PY')$. In both cases we have that $\measuredangle XPY = \measuredangle X'PY'$.

Applying Theorem $\PageIndex{1}$ and Exercise 2.4.2, we get that

$2 \cdot \measuredangle Y'X'P \equiv 2 \cdot \measuredangle Y'X'X \equiv 2 \cdot \measuredangle Y'YX \equiv 2 \dot \measuredangle PYX.$

According to Theorem 3.3.1, $\angle Y'X'P$ and $\angle PYX$ have the same sign; therefore $\measuredangle Y'X'P = \measuredangle PYX$. It remains to apply the AA similarity condition.

(c) Apply (b) assuming $[YY']$ is the diameter of $\Gamma$.

Exercise $\PageIndex{2}$

Three chords $[XX']$, $[YY']$, and $[ZZ']$ of the circle $\Gamma$ intersect at a point $P$. Show that

$XY' \cdot ZX' \cdot YZ' = X'Y \cdot Z'X \cdot Y'Z.$

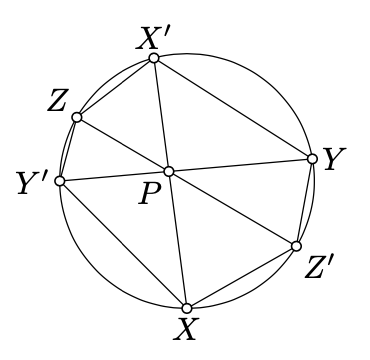
Hint

Apply Exerciese \(\PageIndex{1} b three times.

Exercise $\PageIndex{3}$

Let $\Gamma$ be a circumcircle of an acute triangle $ABC$. Let $A'$ and $B'$ denote the second points of intersection of the altitudes from $A$ and $B$ with $\Gamma$. Show that $\triangle A'B'C$ is isosceles.

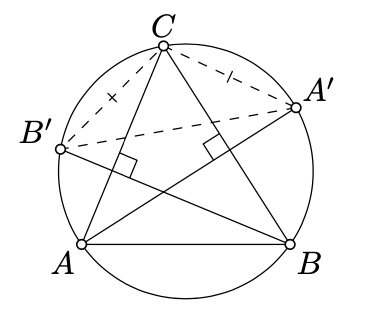
Hint

Let $X$ and $Y$ be the foot points of the altitudes from $A$ and $B$. Suppose that $O$ denotes the circumcenter.

By AA condition, $\triangle AXC \sim \triangle BYC$. Then

$\measuredangle A'OC \equiv 2 \cdot \measuredangle A'AC \equiv - 2 \cdot \measuredangle B'BC \equiv - \measuredangle B'OC.$

By SAS, $\triangle A'OC \cong \triangle B'OC$. Therefore, $A'C = B'C$.

Exercise $\PageIndex{4}$

Let $[XY]$ and $[X'Y']$ be two parallel chords of a circle. Show that $XX' = YY'$.

Exercise $\PageIndex{5}$

Watch “Why is pi here? And why is it squared? A geo- metric answer to the Basel problem” by Grant Sanderson. (It is available on YouTube.)

Prepare one question.