9.1: Angle between a tangent line and a chord
( \newcommand{\kernel}{\mathrm{null}\,}\)
Let Γ be a circle with the center O. Assume the line (XQ) is tangent to Γ at X and [XY] is a chord of Γ. Then
2⋅∡QXY≡∡XOY.
Equivalently,
∡QXY≡12⋅∡XOY or ∡QXY≡12⋅∡XOY+π.
- Proof
-
Note that △XOY is isosceles. Therefore, ∡YXO=∡OYX.
Applying Theorem 7.4.1 to △XOY, we get
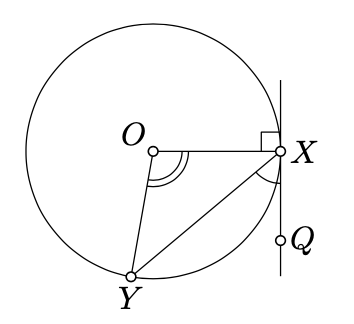
π≡∡YXO+∡OYX+∡XOY≡≡2⋅∡YXO+∡XOY.
By Lemma 5.6.2, (OX)⊥(XQ), Therefore,
∡QXY+∡YXO≡±π2.
Therefore,
2⋅∡QXY≡π−2⋅YXO≡∡XOY.


