16.3: Inversion of the space

Last updated
Save as PDF

Page ID: 23684

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The inversion in a sphere is defined the same way as we define the inversion in a circle.

Formally, let $\Sigma$ be the sphere with the center $O$ and radius $r$. The inversion in $\Sigma$ of a point $P$ is the point $P'\in[OP)$ such that

$OP\cdot OP'=r^2.$

In this case, the sphere $\Sigma$ will be called the sphere of inversion and its center is called the center of inversion.

We also add $\infty$ to the space and assume that the center of inversion is mapped to $\infty$ and the other way around. The space $\mathbb{R}^3$ with the point $\infty$ will be called inversive space.

The inversion of the space has many properties of the inversion of the plane. Most important for us are the analogs of Theorem 10.2.1, Theorem 10.3.1 and Theorem 10.6.1 which can be summarized as follows:

Theorem $\PageIndex{1}$

The inversion in the sphere has the following properties:

Inversion maps a sphere or a plane into a sphere or a plane.
Inversion maps a circle or a line into a circle or a line.
Inversion preserves the cross-ratio; that is, if $A'$, $B'$, $C'$, and $D'$ are the inverses of the points $A$, $B$, $C$ and $D$ respectively, then \[\dfrac{AB\cdot CD}{BC\cdot DA}= \dfrac{A'B'\cdot C'D'}{B'C'\cdot D'A'}.\]
Inversion maps arcs into arcs.
Inversion preserves the absolute value of the angle measure between tangent half-lines to the arcs.

We do not present the proofs here, but they nearly repeat the corresponding proofs in plane geometry. To prove (a), you will need in addition the following lemma; its proof is left to the reader.

Lemma $\PageIndex{1}$

Let $\Sigma$ be a subset of the Euclidean space that contains at least two points. Fix a point $O$ in the space.

Then $\Sigma$ is a sphere if and only if for any plane $\Pi$ passing thru $O$, the intersection $\Pi \cap \Sigma$ is either empty set, one point set or a circle.

The following observation helps to reduce part (b) to part (a).

Observation $\PageIndex{1}$

Any circle in the space is an intersection of two spheres.

Let us define a circular cone as a set formed by line segments from a fixed point, called the tip of the cone, to all the points on a fixed circle, called the base of the cone; we always assume that the base does not lie in the same plane as the tip. We say that the cone is right if the center of the base circle is the foot point of the tip on the base plane; otherwise we call it oblique.

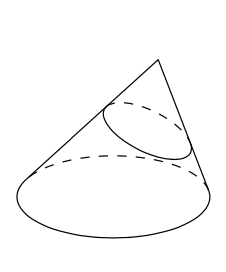
$截屏2021-03-01 上午10.14.22.png$

Exercise $\PageIndex{1}$

Let $K$ be an oblique circular cone. Show that there is a plane $\Pi$ that is not parallel to the base plane of $K$ such that the intersection $\Pi\cap K$ is a circle.

Hint: Consider the inversion of the base in a sphere with the center at the tip of the cone and apply Theorem $\PageIndex{1}$.

Theorem \(\PageIndex{1}\)

Lemma \(\PageIndex{1}\)

Observation \(\PageIndex{1}\)

Exercise \(\PageIndex{1}\)