4.2: Similar Triangles
- Page ID
- 34136
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
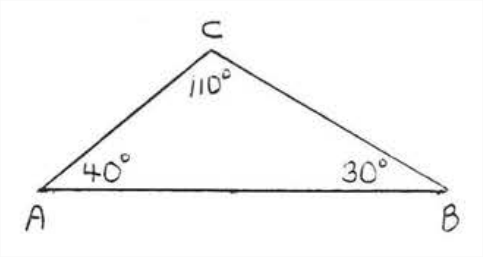
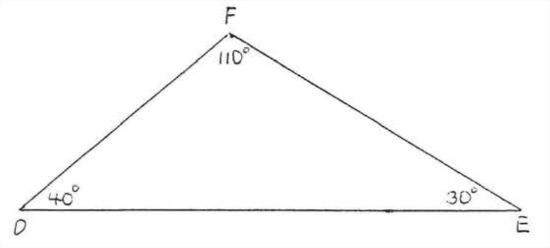
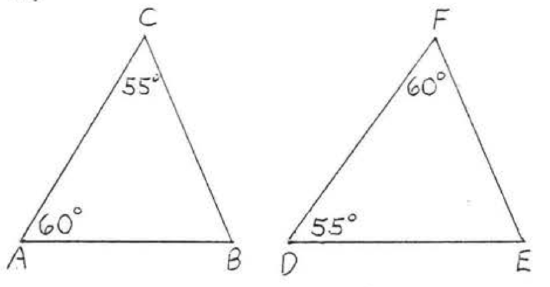
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two triangles are said to be similar if they have equal sets of angles. In Figure \(\PageIndex{1}\), \(\triangle ABC\) is similar to \(\triangle DEF.\) The angles which are equal are called corresponding angles. In Figure \(\PageIndex{1}\), \(\angle A\) corresponds to \(\angle D\), \(\angle B\) corresponds to \(\angle E\), and \(\angle C\) corresponds to \(\angle F\). The sides joining corresponding vertices are called corresponding sides. In Figure \(\PageIndex{1}\), \(AB\) corresponds to \(DE\), \(BC\) corresponds to \(EF\), and \(AC\) corresponds to \(DF\). The symbol for similar is \(\sim\). The similarity statement \(\triangle ABC \sim \triangle DEF\) will always be written so that corresponding vertices appear in the same order.
For the triangles in Figure \(\PageIndex{1}\), we could also write \(\triangle BAC \sim \triangle BDF\) or \(\triangle ACB \sim \triangle DFE\) but never \(\triangle ABC \sim \triangle EDF\) nor \(\triangle ACB \sim \triangle DEF\).
We can tell which sides correspond from the similarity statement. For example, if \(\triangle ABC \sim \triangle DEF\), then side \(AB\) corresponds to side \(DE\) because both are the first two letters. \(BC\) corresponds to \(EF\) because both are the last two letters, \(AC\) corresponds to \(DF\) because both consist of the first and last letters.
Determine if the triangles are similar, and if so, write the similarity statement:
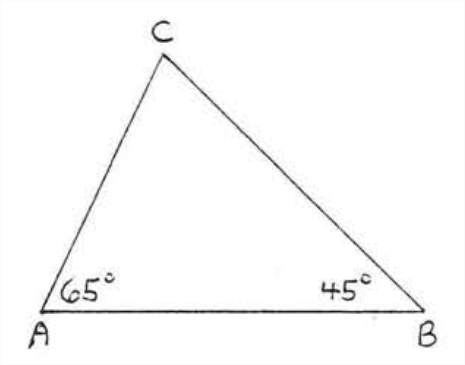
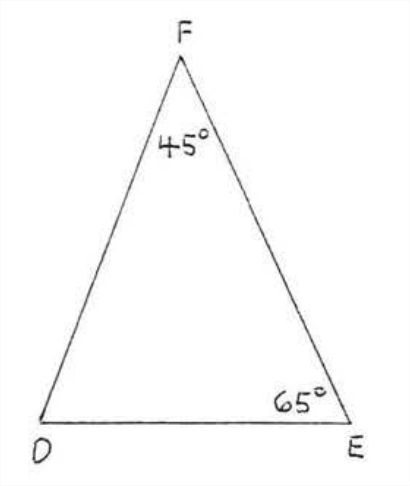
Solution
\[\angle C = 180^{\circ} - (65^{\circ} + 45^{\circ}) = 180^{\circ} - 110^{\circ} = 70^{\circ} \nonumber\]
\[\angle D = 180^{\circ} - (65^{\circ} + 45^{\circ}) = 180^{\circ} - 110^{\circ} = 70^{\circ} \nonumber\]
Therefore both triangles have the same angles and \(\triangle ABC \sim \triangle EFD\).
Answer: \(\triangle ABC \sim \triangle EFD\).
Example A suggests that to prove similarity it is only necessary to know that two of the corresponding angles are equal:
Two triangles are similar if two angles of one equal two angles of the other \((AA = AA)\).
In Figure \(\PageIndex{2}\), \(\triangle ABC \sim \triangle DEF\) because \(\angle A = \angle D\) and \(\angle B = \angle E\).
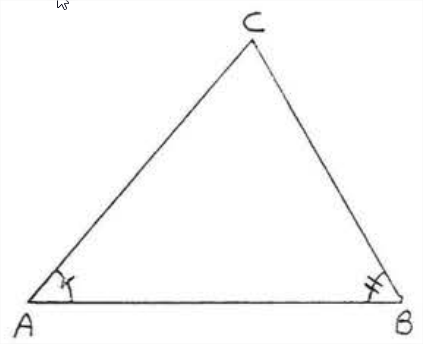
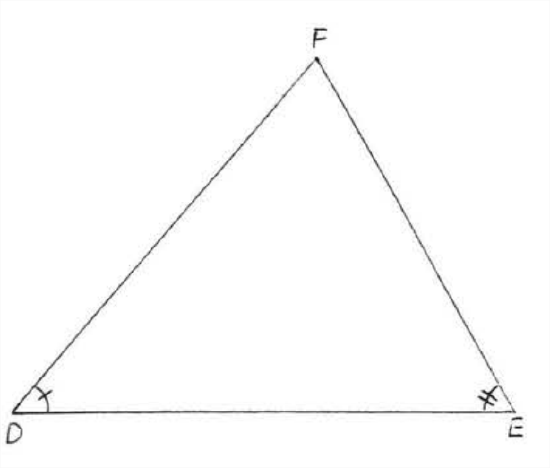
- Proof
-
\(\triangle C = 180^{\circ} - (\angle A + \angle B) = 180^{\circ} - (\angle D + \angle E) = \angle F\).
Determine which triangles are similar and write a similarity statement:
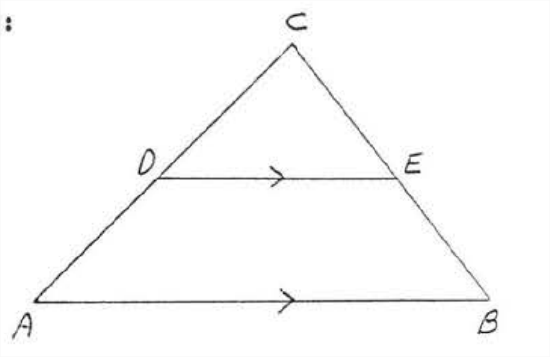
Solution
\(\angle A = \angle CDE\) because they are corresponding angles of parallel lines. \(\angle C = \angle C\) because of identity. Therefore \(\triangle ABC \sim \triangle DEC\) by \(AA = AA\).
Answer: \(\triangle ABC \sim \triangle DEC\).
Determine which triangles are similar and write a similarity statement:
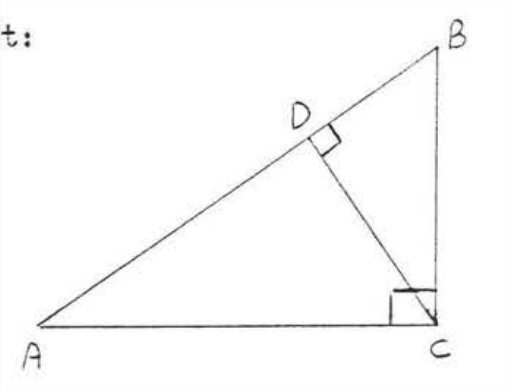
Solution
\(\angle A=\angle A\) identity. \(\angle ACB = \angle ADC=90^{\circ}\). Therefore
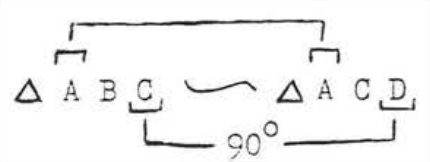
Also \(\angle B = \angle B\), identity, \(\angle BDC = \angle BCA = 90^{\circ}\). Therefore
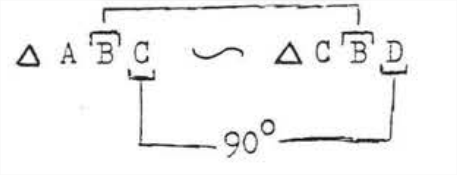
Answer: \(\triangle ABC \sim \triangle ACD \sim \triangle CBD\).
Similar triangIes are important because of the following theorem:
The corresponding sides of similar triangles are proportional. This means that if \(\triangle ABC \sim \triangle DEF\) then
\(\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}\).
That is, the first two letters of \(\triangle ABC\) are to the first two letters of \(\triangle DEF\) as the last two letters of \(\triangle ABC\) are to the last two letters of \(\triangle DEF\) as the first and last letters of \(\triangle ABC\) are to the first and last letters of \(\triangle DEF\).
Before attempting to prove Theorem \(\PageIndex{2}\), we will give several examples of how it is used:
Find \(x\):
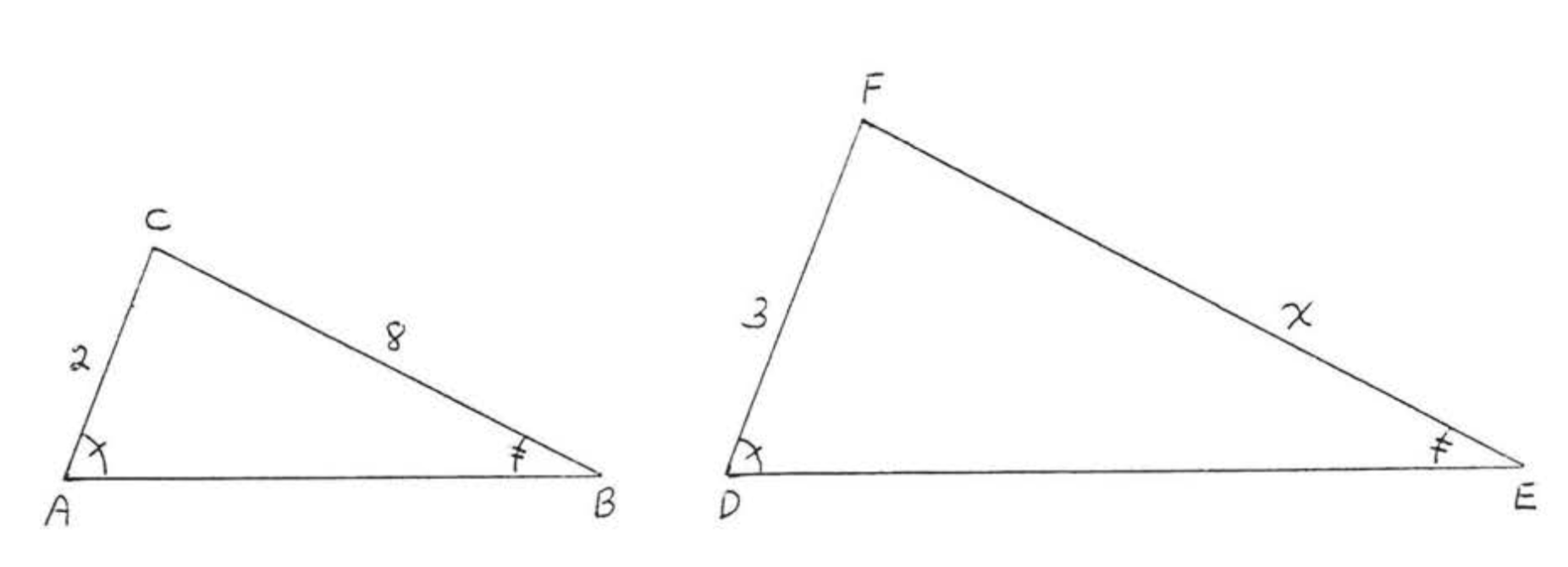
Solution
\(\angle A = \angle D\) and \(\angle B = \angle E\) so \(\triangle ABC \sim \triangle DEF\). By Theorem \(\PageIndex{2}\),
\(\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}\).
We will ignore \(\dfrac{AB}{DE}\) here since we do not know and do not have to find either \(AB\) or \(DE\).
\[\begin{array} {rcl} {\dfrac{BC}{EF}} & = & {\dfrac{AC}{DF}} \\ {\dfrac{8}{x}} & = & {\dfrac{2}{3}} \\ {24} & = & {2x} \\ {12} & = & {x} \end{array}\]
Check:
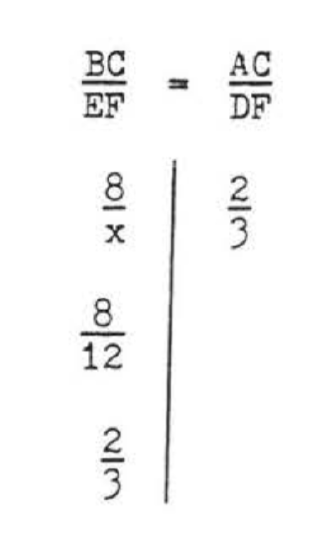
Answer: \(x = 12\).
Find \(x\):
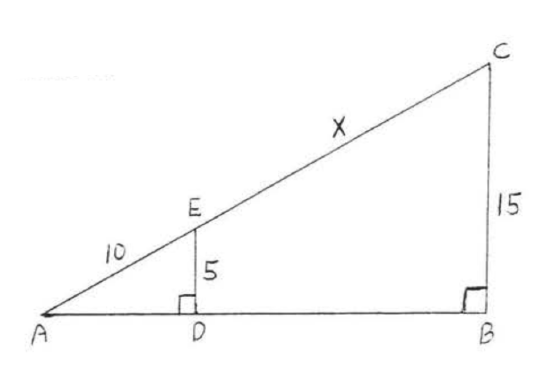
Solution
\(\angle A = \angle A, \angle ADE = \angle ABC\), so \(\triangle ADE \sim \triangle ABC\) by \(AA = AA\).
\(\dfrac{AD}{AB} = \dfrac{DE}{BC} = \dfrac{AE}{AC}\).
We ignore \(\dfrac{AD}{AB}\).
\[\begin{array} {rcl} {\dfrac{DE}{BC}} & = & {\dfrac{AE}{AC}} \\ {\dfrac{5}{15}} & = & {\dfrac{10}{10 + x}} \\ {5(10 + x)} & = & {15(10)} \\ {50 + 5x} & = & {150} \\ {5x} & = & {150 - 50} \\ {5x} & = & {100} \\ {x} & = & {20} \end{array}\]
Check:
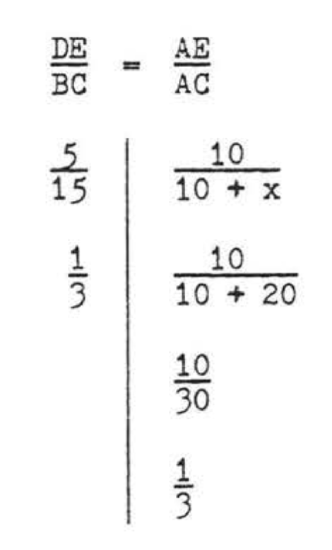
Answer: \(x = 20\).
Find \(x\):
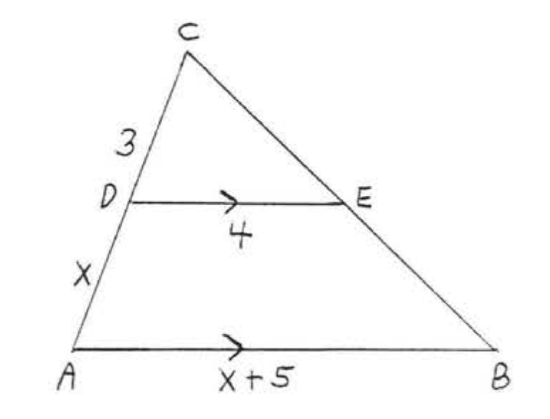
Solution
\(\angle A = \angle CDE\) because they are corresponding angles of parallel lines. \(\angle C = \angle C\) because of identity. Therefore \(\triangle ABC \sim \triangle DEC\) by \(AA = AA\).
\(\dfrac{AB}{DE} = \dfrac{BC}{EC} = \dfrac{AC}{DC}\)
We ignore \(\dfrac{BC}{EC}\):
\[\begin{array} {rcl} {\dfrac{AB}{DE}} & = & {\dfrac{AC}{DC}} \\ {\dfrac{x + 5}{4}} & = & {\dfrac{x + 3}{3}} \\ {(x + 5)(3)} & = & {(4)(x + 3)} \\ {3x + 15} & = & {4x + 12} \\ {15 - 12} & = & {4x - 3x} \\ {3} & = & {x} \end{array}\]
Check:
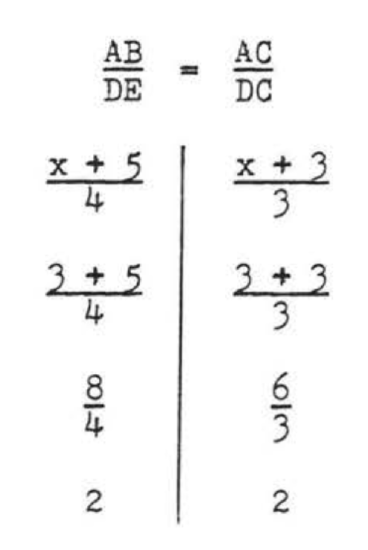
Answer: \(x = 3\).
Find \(x\):
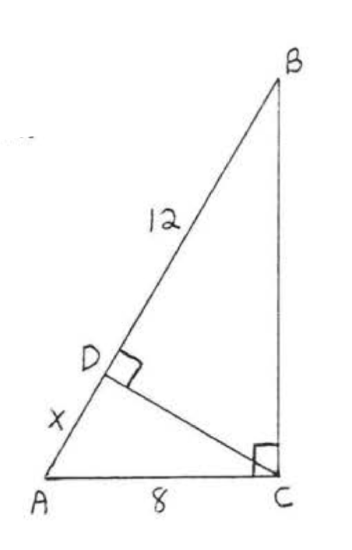
Solution
\(\angle A = \angle A\), \(\angle ACB = \angle ADC = 90^{\circ}\), \(\triangle ABC \sim \triangle ACD\).
\[\begin{array} {rcl} {\dfrac{AB}{AC}} & = & {\dfrac{AC}{AD}} \\ {\dfrac{x + 12}{8}} & = & {\dfrac{8}{x}} \\ {(x + 12)(x)} & = & {(8)(8)} \\ {x^2 + 12x} & = & {64} \\ {x^2 + 12x - 64} & = & {0} \\ {(x - 4)(x + 16)} & = & {0} \\ {x = 4\ \ \ \ \ \ \ \ x} & = & {-16} \end{array}\]
We reject the answer \(x = -16\) because \(AD = x\) cannot be negative.
Check, \(x = 4\)

Answer: \(x = 4\).
A tree casts a shadow 12 feet long at the same time a 6 foot man casts a shadow 4 feet long. What is the height of the tree?
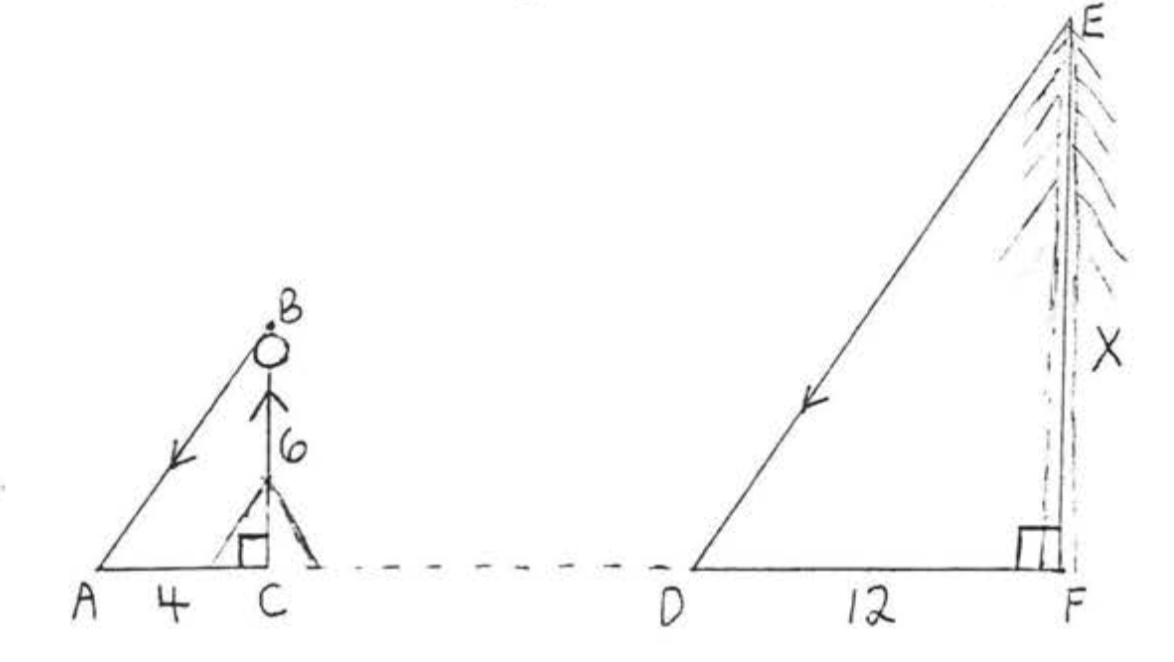
Solution
In the diagram \(AB\) and \(DE\) are parallel rays of the sun. Therefore \(\angle A = \angle D\) because they are corresponding angles of parallel lines with respect to the transversal \(AF\). Since also \(\angle C = \angle F = 90^{\circ}\), we have \(\triangle ABC \sim \triangle DEF\) by \(AA = AA\).
\[\begin{array} {rcl} {\dfrac{AC}{DF}} & = & {\dfrac{BC}{EF}} \\ {\dfrac{4}{12}} & = & {\dfrac{6}{x}} \\ {4x} & = & {72} \\ {x} & = & {18} \end{array}\]
Answer: \(x = 18\) feet.
Proof of Theorem \(\PageIndex{2}\) ("The corresponding sides of similar triangles are proportional"):
We illustrate the proof using the triangles of Example \(\PageIndex{4}\) (Figure \(\PageIndex{3}\)). The proof for other similar triangles follows the same pattern. Here we will prove that \(x = 12\) so that \(\dfrac{2}{3} = \dfrac{8}{x}\).

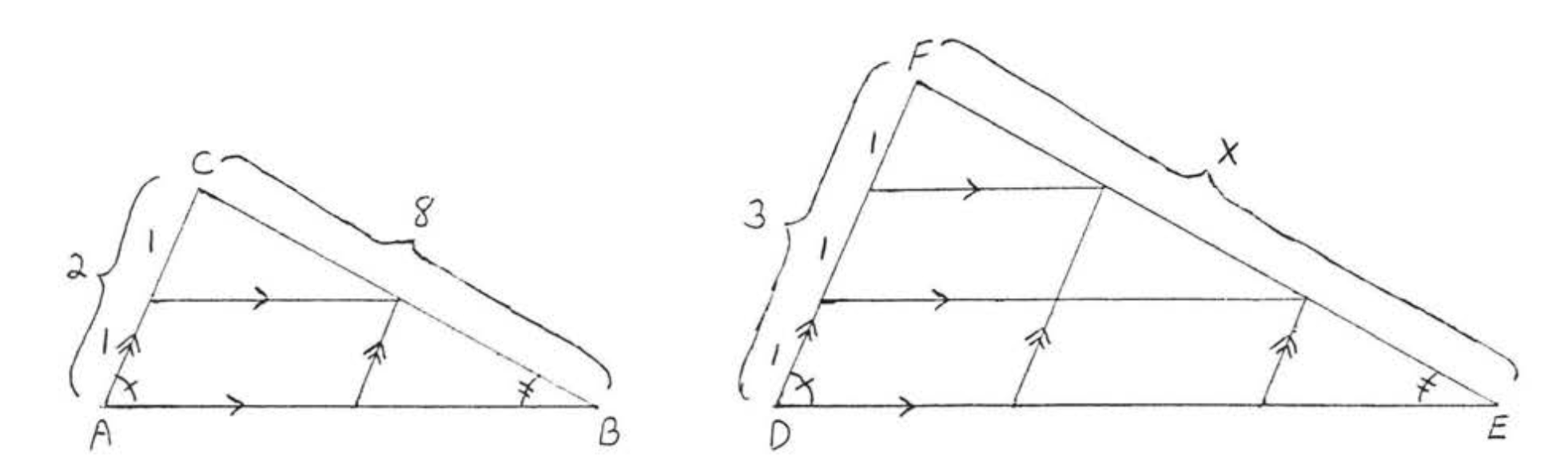
First draw lines parallel to the sides of \(\triangle ABC\) and \(\triangle DEF\) as shown in Figure \(\PageIndex{4}\). The corresponding angles of these parallel lines are equal and each of the parallelograms with a side equal to 1 has its opposite side equal to 1 as well, Therefore all of the small triangles with a side equal to 1 are congruent by \(AAS = AAS\). The corresponding sides of these triangles form side \(BC = 8\) of \(\triangle ABC\) (see Figure \(\PageIndex{5}\)). Therefore each of these sides must equal 4 and \(x = EF = 4 + 4 + 4 = 12\) (Figure \(\PageIndex{6}\)).
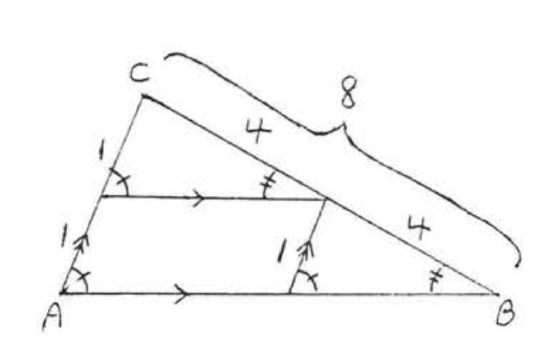
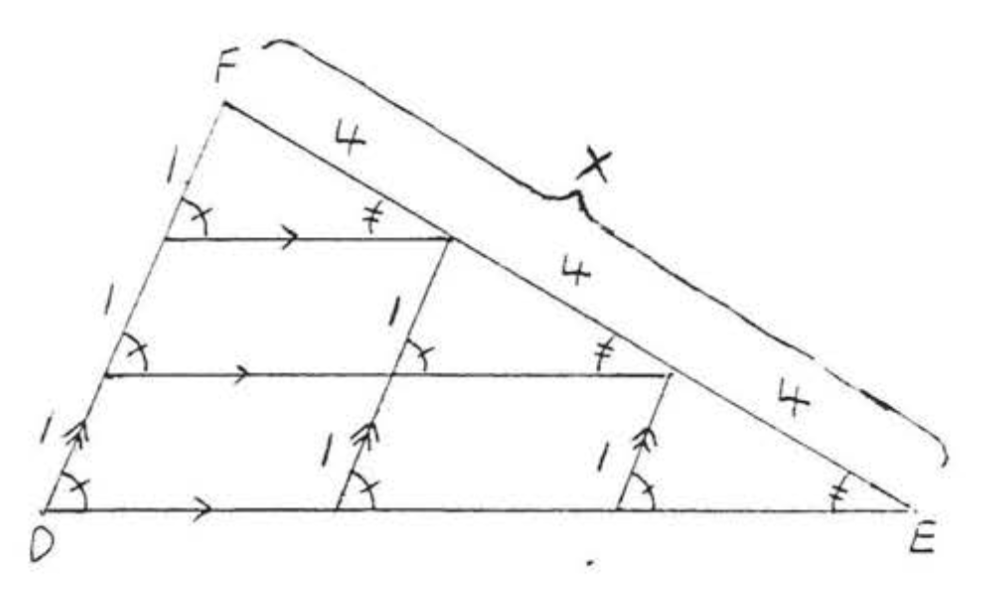
(Note to instructor: This proof can be carried out whenever the lengths of the sides of the triangles are rational numbers. However, since irrational numbers can be approximated as closely as necessary by rationals, the proof extends to that case as well.)
Thales (c. 600 B.C.) used the proportionality of sides of similar triangles to measure the heights of the pyramids in Egypt. His method was much like the one we used in Example \(\PageIndex{8}\) to measure the height of trees.
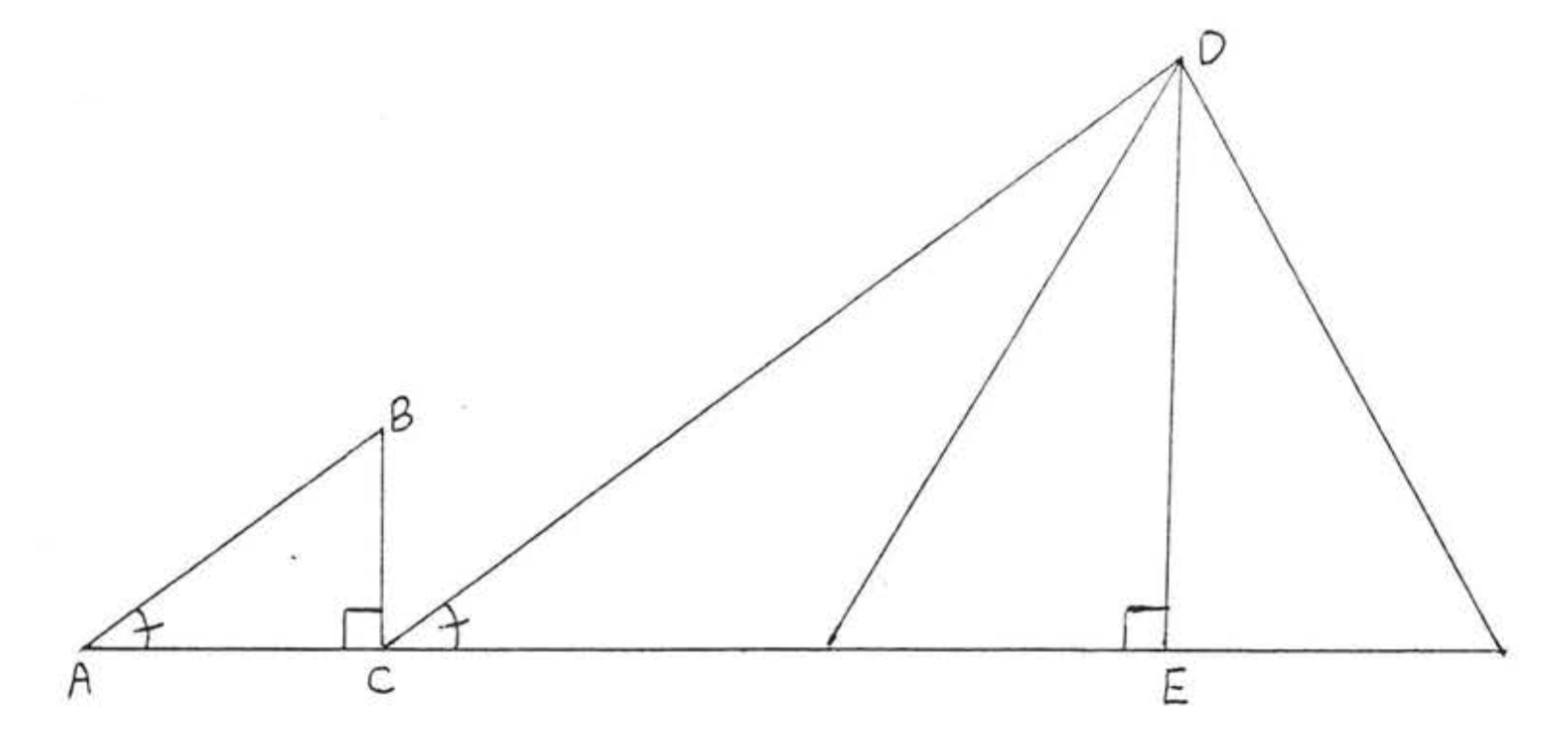
In Figure \(\PageIndex{7}\), \(DE\) represent the height of the pyramid and \(CE\) is the length of its shadow. \(BC\) represents a vertical stick and \(AC\) is the length of its shadow. We have \(\triangle ABC \sim \triangle CDE\). Thales was able to measure directly the lengths \(AC, BC\), and \(CE\). Substituting these values in the proportion \(\dfrac{BC}{DE} = \dfrac{AC}{CE}\), he was able to find the height \(DE\).
Problems
1 - 6. Determine which triangles are similar and write the similarity statement:
1.
2.
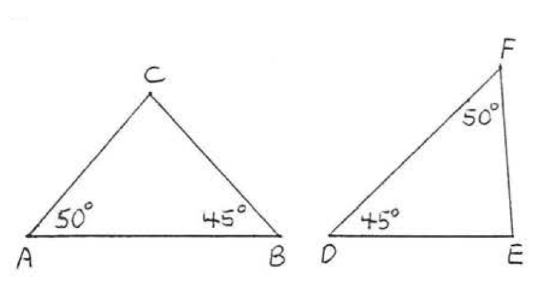
3.
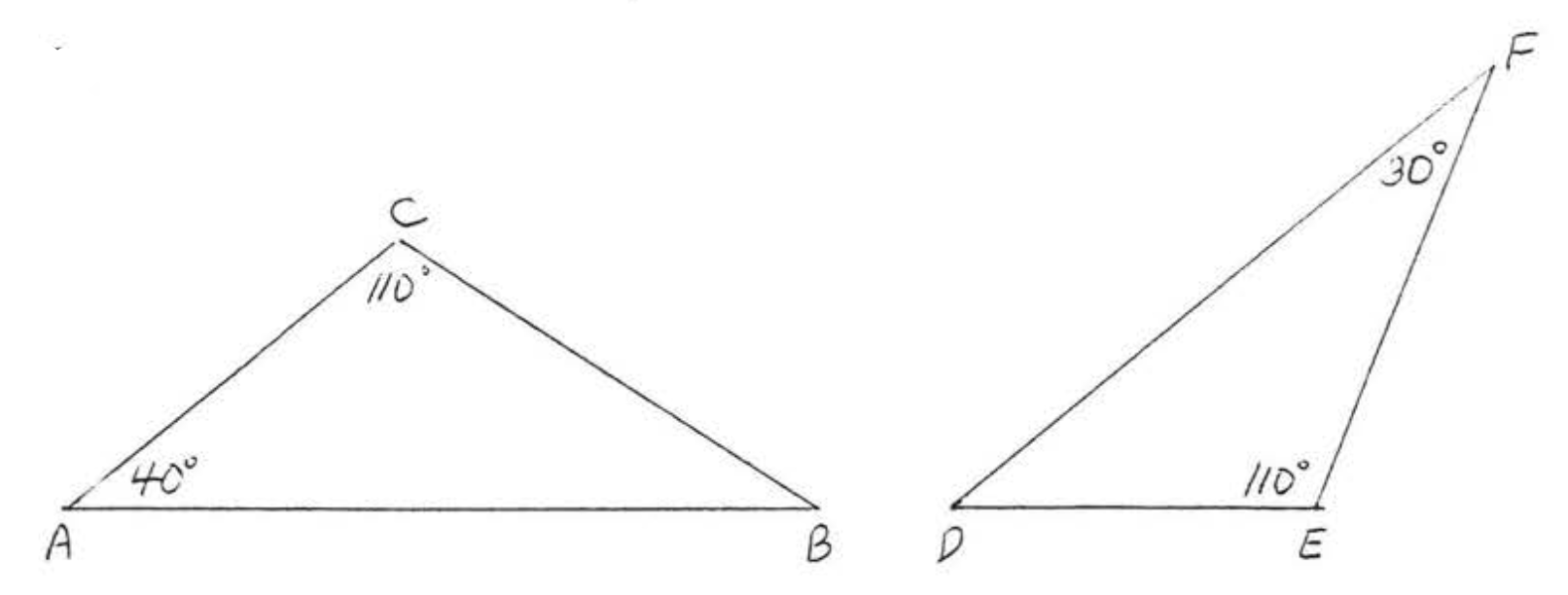
4. 
5.
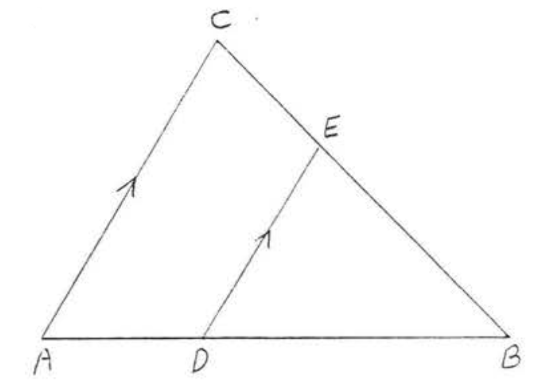
6.

7 - 22. For each of the following
(1) write the similarity statement
(2) write the proportion between the corresponding sides
(3) solve for \(x\) or \(x\) and \(y\).
7.
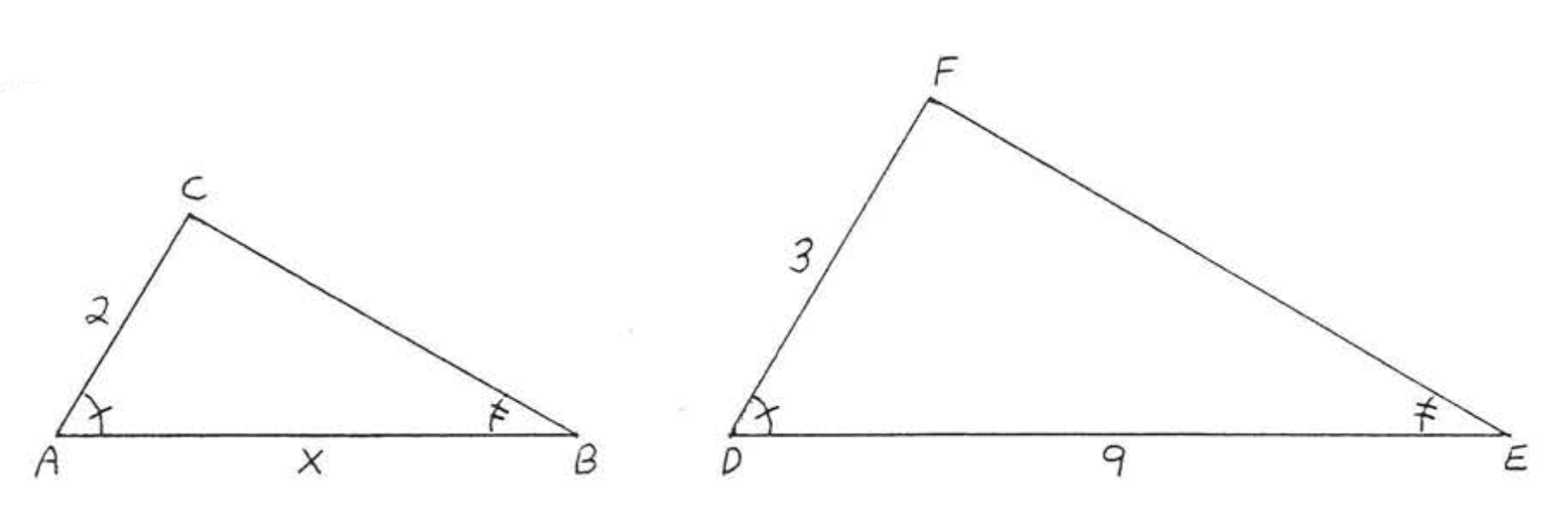
8.
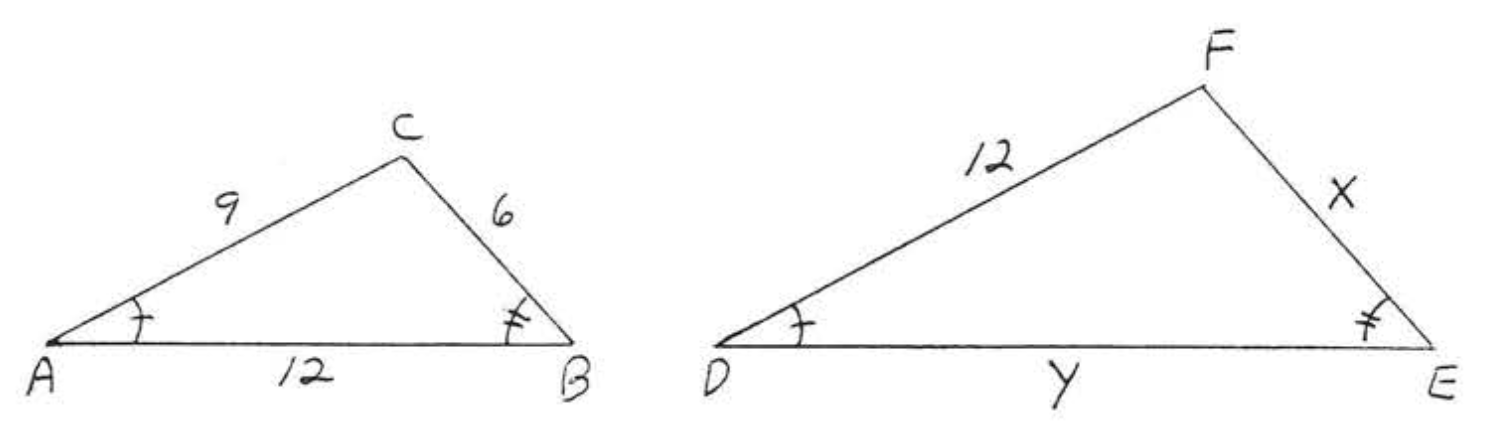
9.
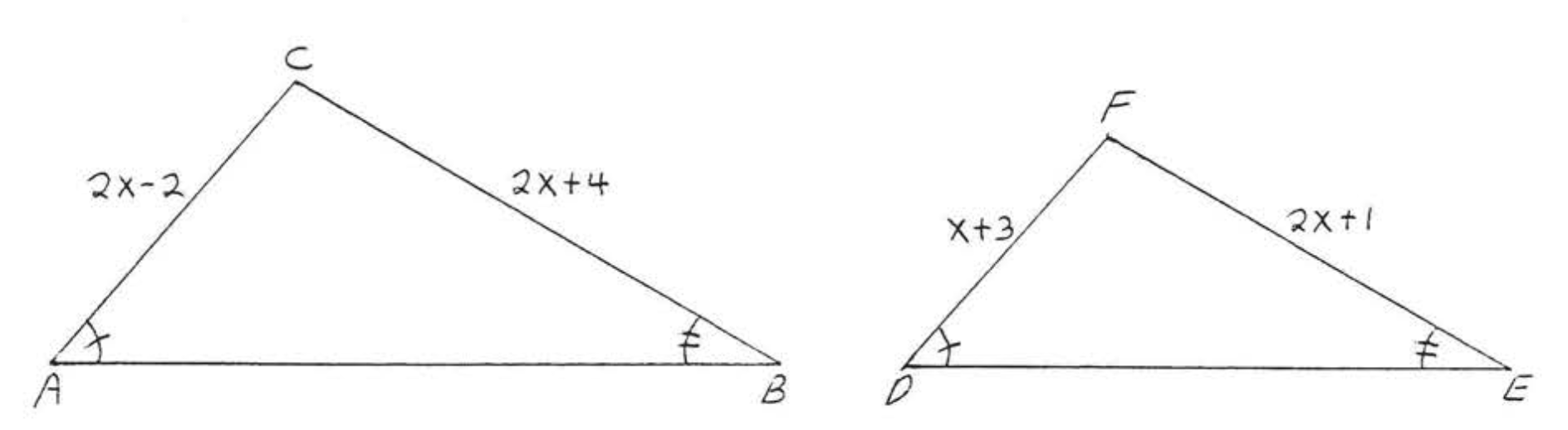
10.
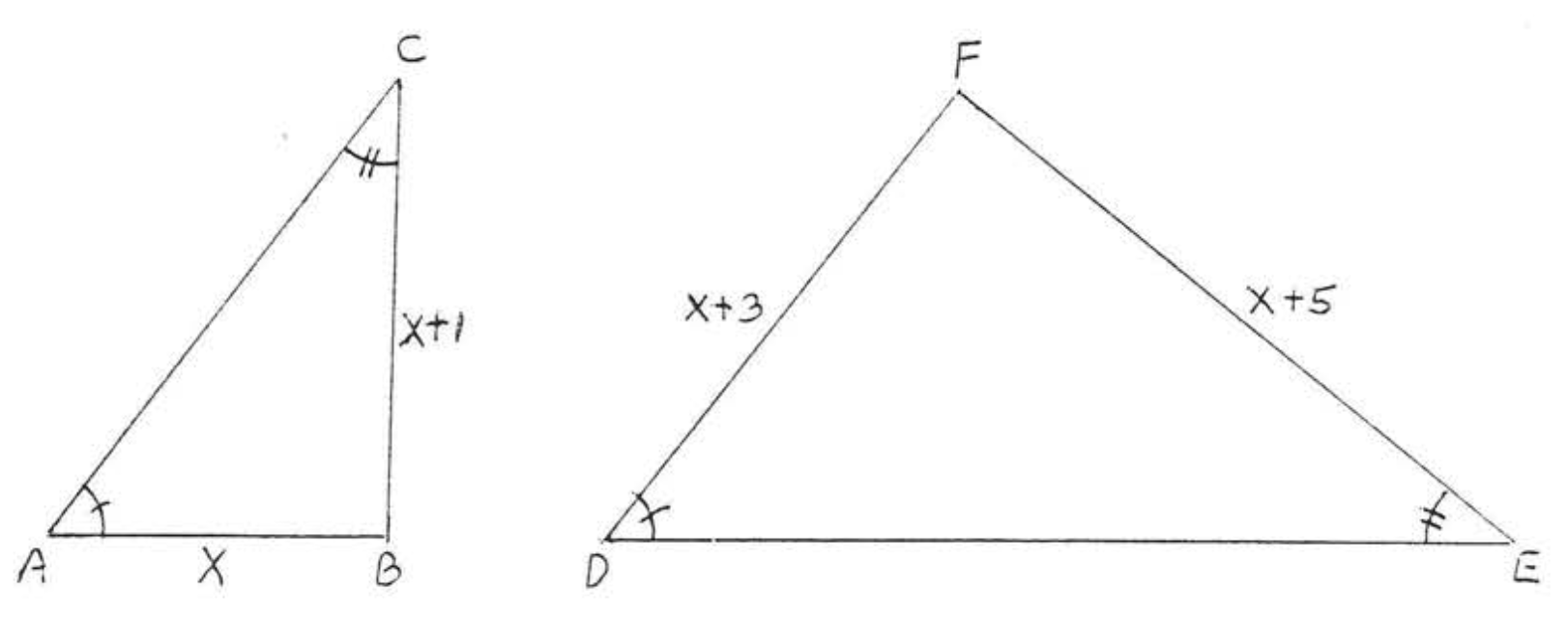
11.
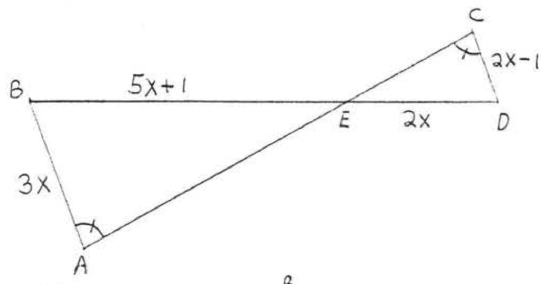
12.
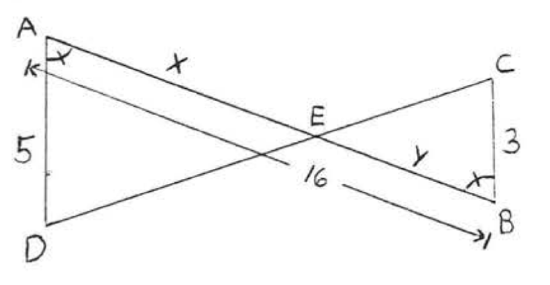
13.
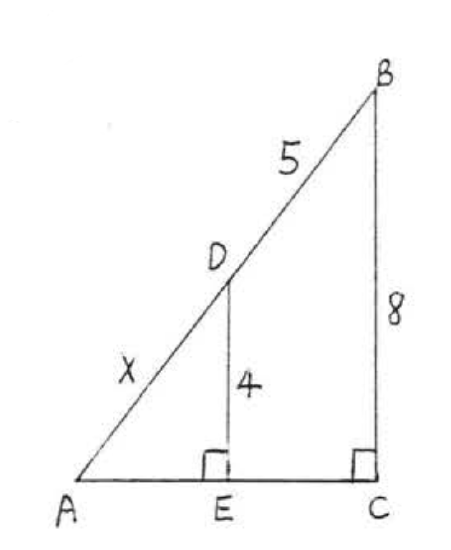
14.
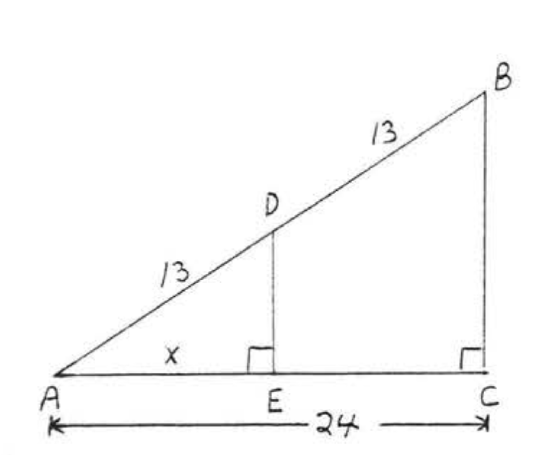
15.
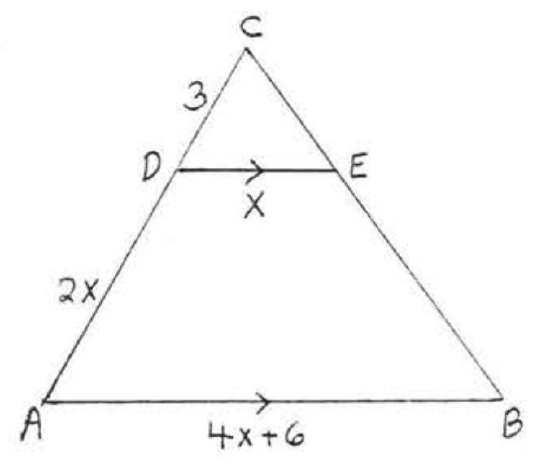
16.
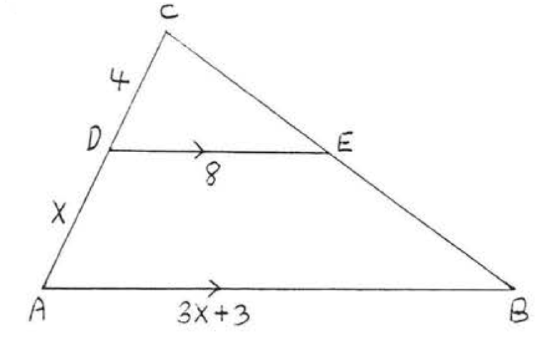
17.
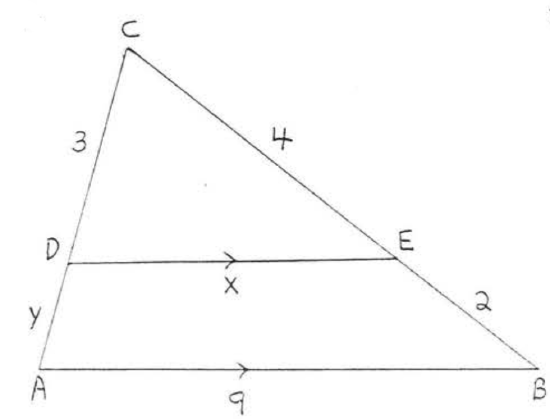
18.
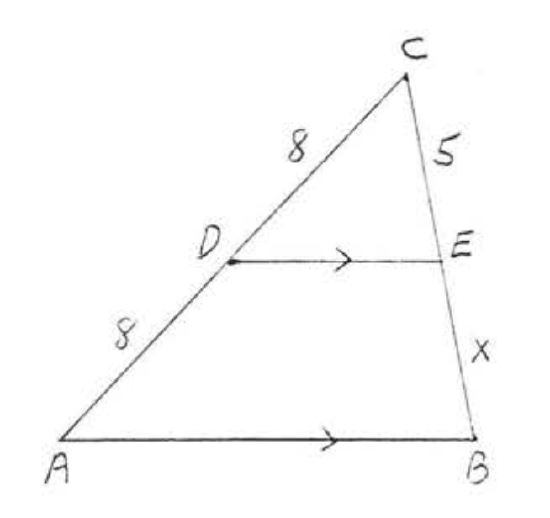
19.
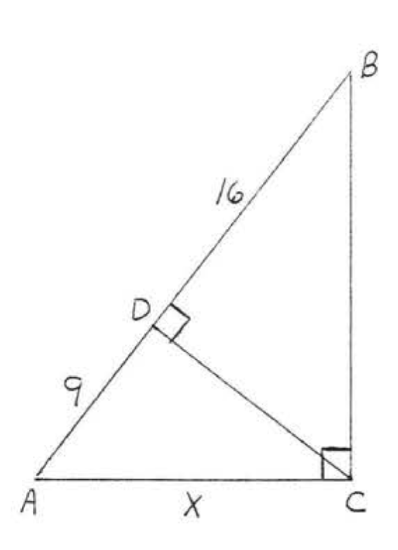
20.
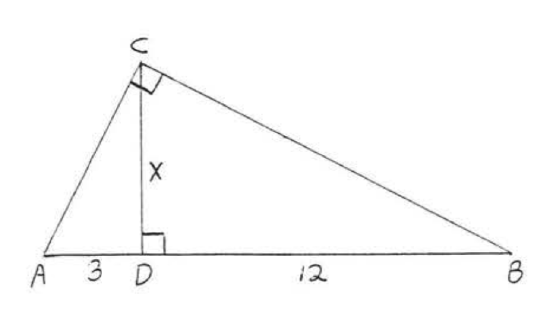
21.
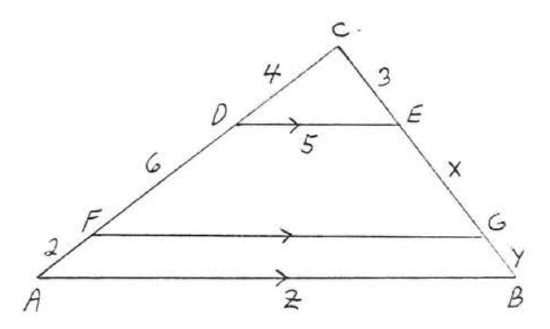
22.
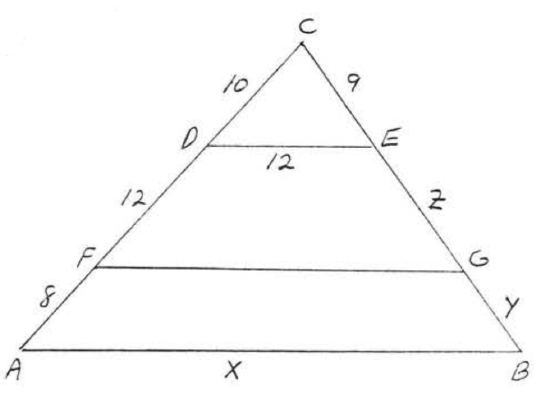
23. A flagpole casts a shadow 80 feet long at the same time a 5 foot boy casts a shadow 4 feet long. How tall is the flagpole?
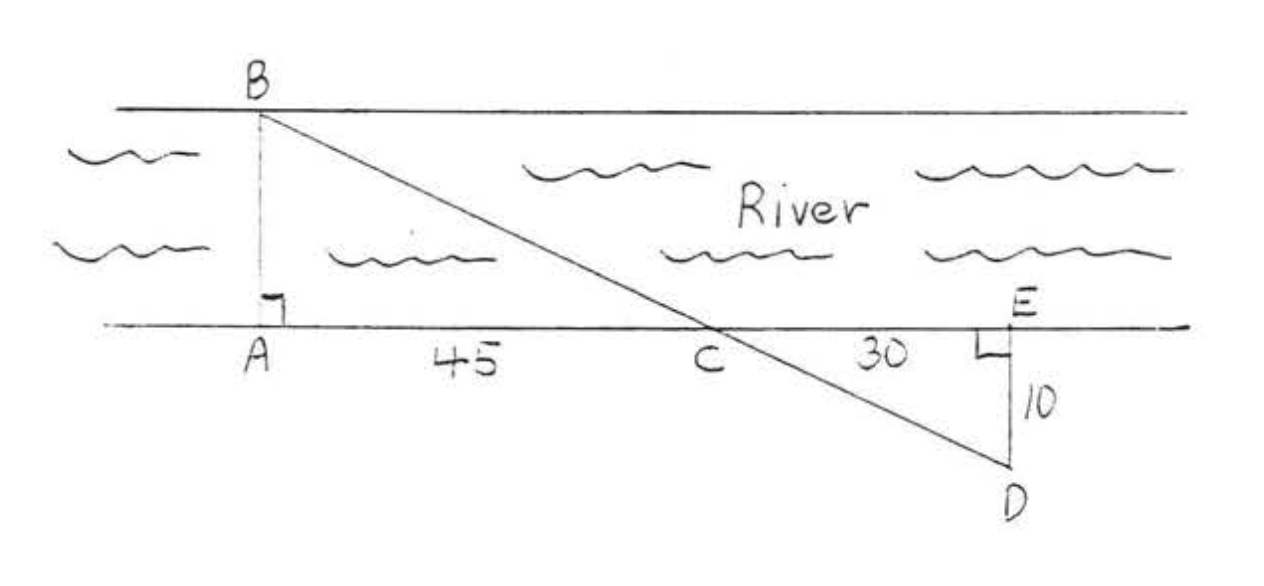
24. Find the width \(AB\) of the river: