4.3: Transversals to Three Parallel Lines
- Page ID
- 34137
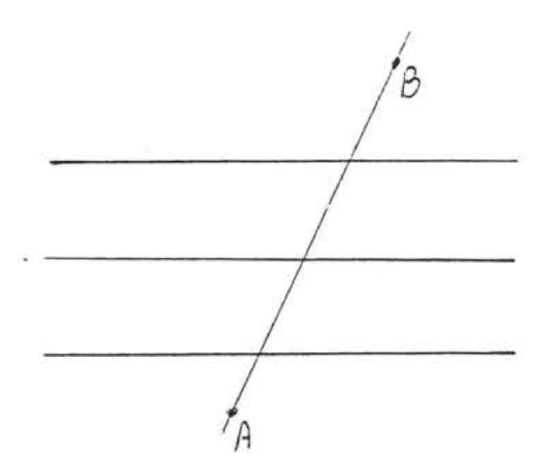
In Chapter 1 we defined a transversal to be a line which intersects two other lines, We will now extend the definition to a line which intersects three other lines. In Figure \(\PageIndex{1}\), \(AB\) is a transversal to three lines.
If the three lines are parallel and we have two such transversals we may state the following theorem:
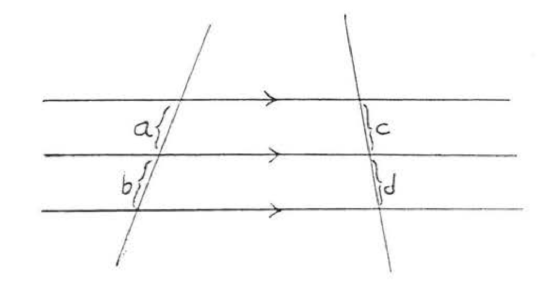
The line segments formed by two transversals crossing three parallel lines are proportional.
In Figure \(\PageIndex{2}\), \(\dfrac{a}{b} = \dfrac{c}{d}\).
Find \(x\):
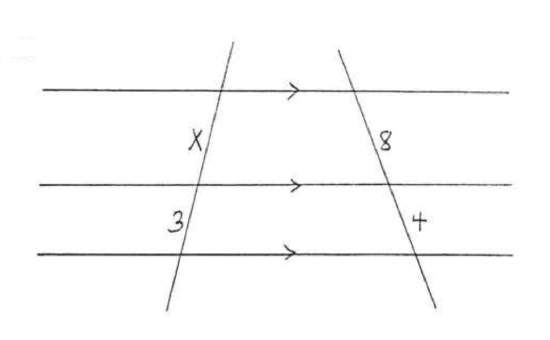
Solution
\[\begin{array} {rcl} {\dfrac{x}{3}} & = & {\dfrac{8}{4}} \\ {4x} & = & {24} \\ {x} & = & {6} \end{array}\]
Check:
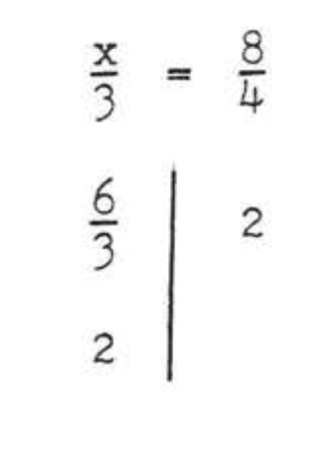
Answer: \(x = 6\).
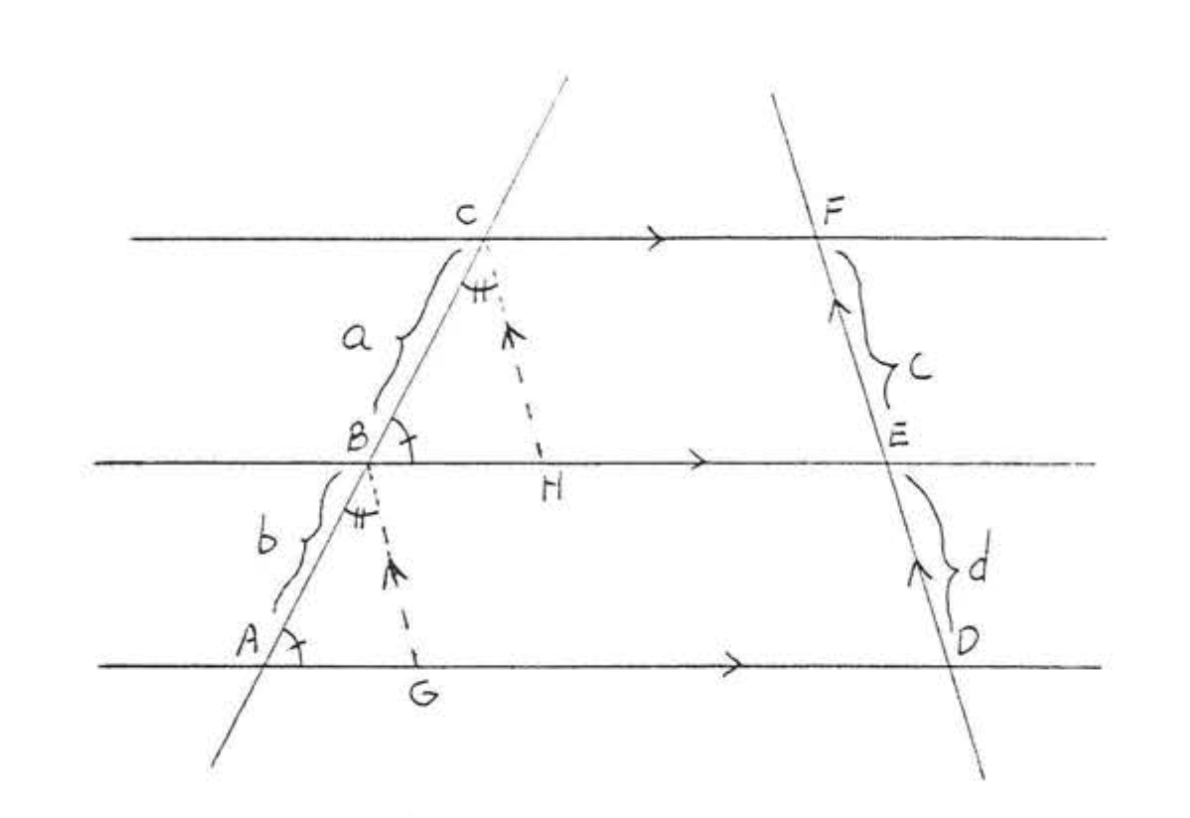
Draw \(GB\) and \(HC\) parallel to \(DF\) (Figure \(\PageIndex{3}\)). The corresponding angles of the parallel lines are equal and so \(\triangle BCH \sim \triangle ABG\). Therefore
\[\dfrac{BC}{AB} = \dfrac{CH}{BG}.\]
Now \(CH = FE = c\) and \(BG = ED = d\) because they are the opposite sides of a parallelogram. Substituting, we obtain
\[\dfrac{a}{b} = \dfrac{c}{d}.\]
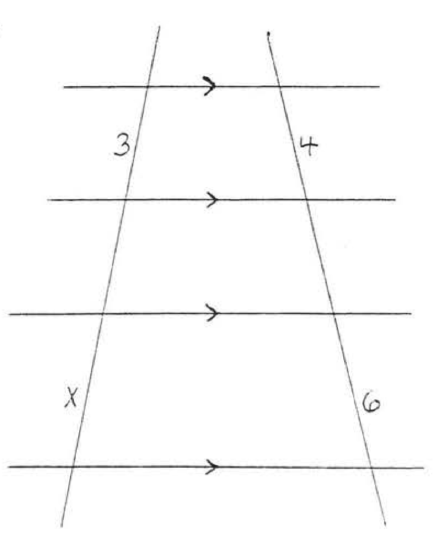
Find \(x\):
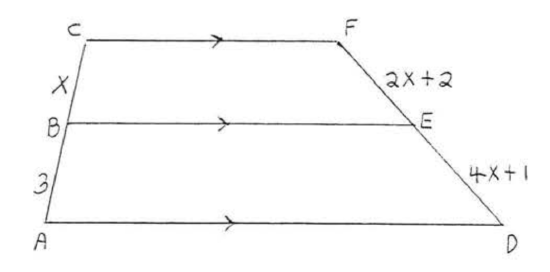
Solution
\(\begin{array} {rcl} {\dfrac{x}{3}} & = & {\dfrac{2x + 2}{4x + 1}} \\ {(x)(4x + 1)} & = & {(3)(2x + 2)} \\ {4x^2 + x} & = & {6x + 6} \\ {4x^2 - 5x - 6} & = & {0} \\ {(x - 2)(4x + 3)} & = & {0} \end{array}\)
\(\begin{array} {rcl} {x - 2} & = & {0} \\ {x} & = & {-2} \end{array}\) or \(\begin{array} {rcl} {4x + 3} & = & {0} \\ {4x} & = & {-3} \\ {x} & = & {-\dfrac{3}{4}} \end{array}\)
We reject \(x = -\dfrac{3}{4}\) because \(BC = x\) cannot be negative.
Check, \(x = 2\):
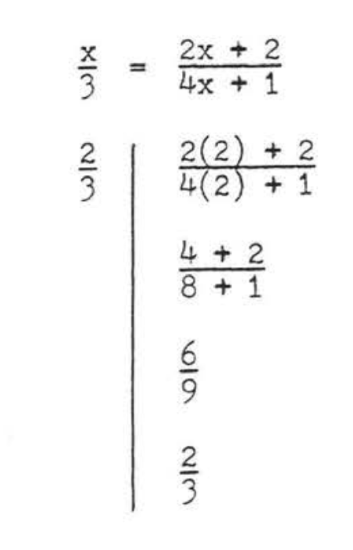
Answer: \(x = 2\).
Problems
1 - 6. Find \(x\):
1.
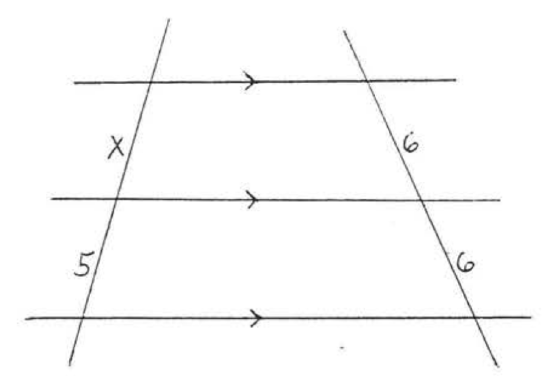
2.
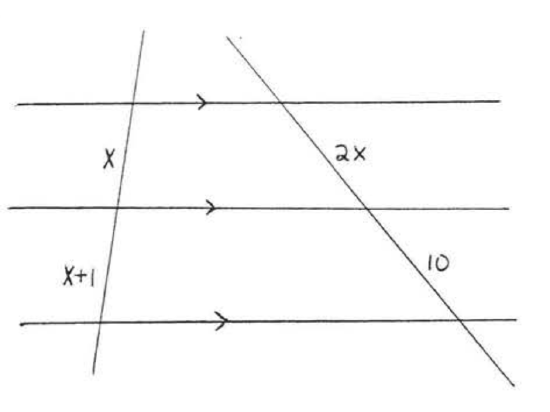
3.
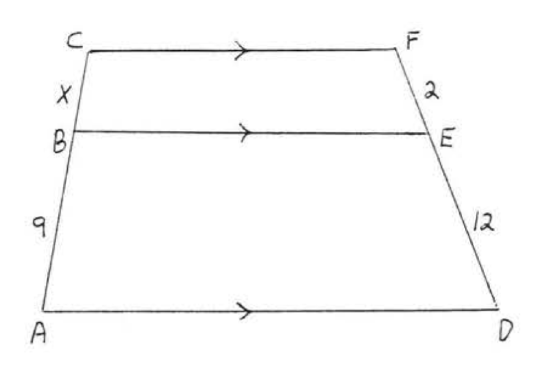
4.
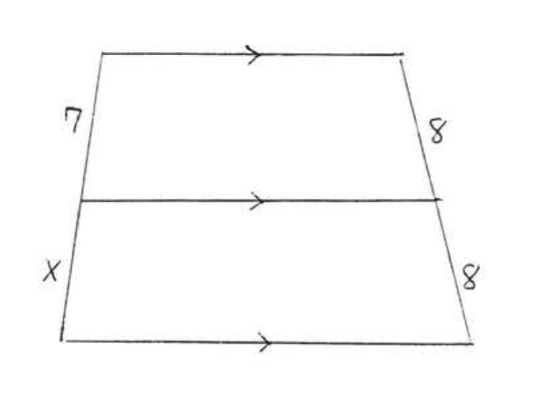
5.
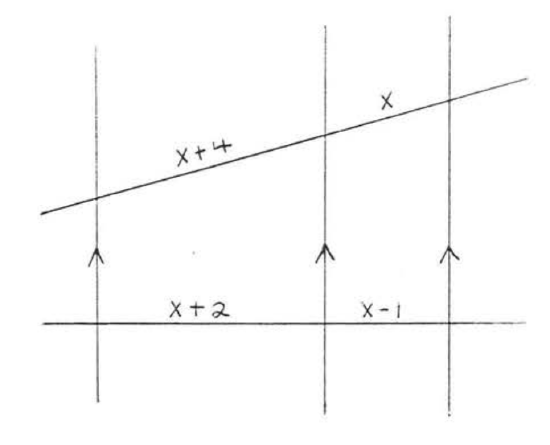
6.