5.1: The Trigonometric Functions
- Page ID
- 34142
Trigonometry (from Greek words meaning triangle-measure) is the branch of mathematics concerned with computing unknown sides and angles of triangles. For example, in Figure \(\PageIndex{1}\), we might want to measure the height of the tree without actually having to climb the tree. The methods of trigonometry will enable us to do this.
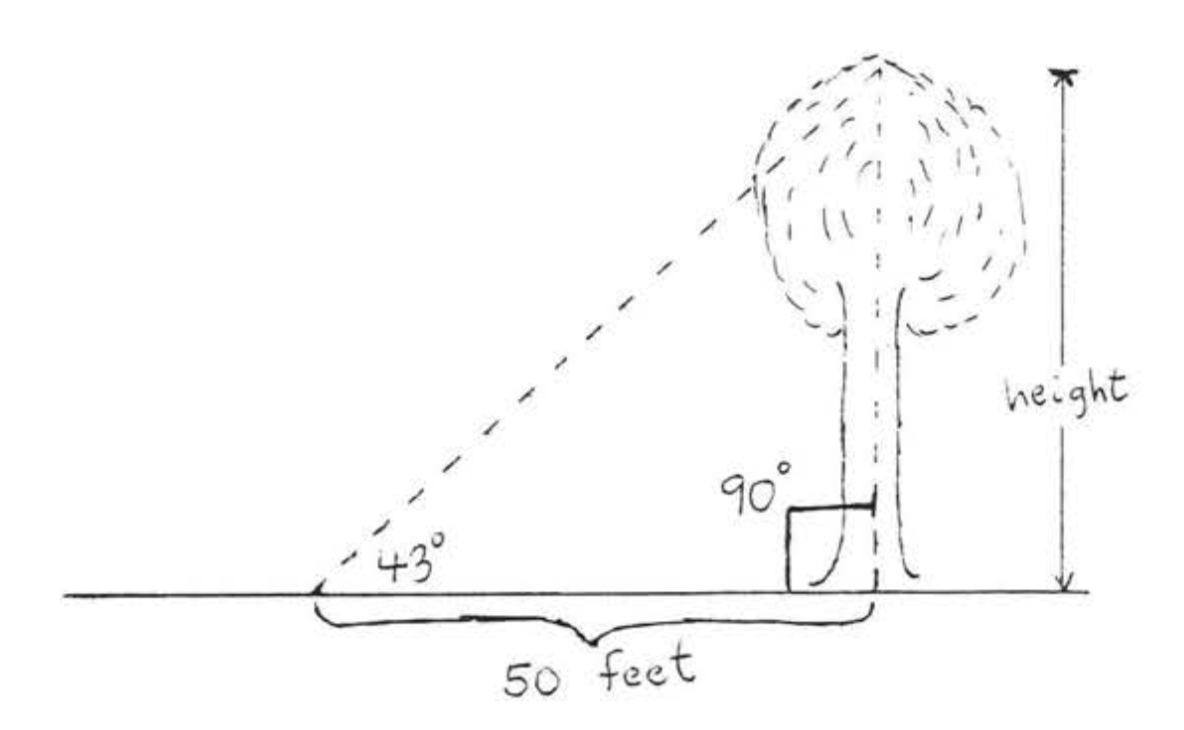
In this book we will consider just the trigonometry of the right triangle. In more advanced courses, trigonometry deals with other kinds of triangles as well. Here, however, the following definitions apply only to right triangles.
In right triangle \(ABC\) of Figure \(\PageIndex{2}\), \(AC\) is called the leg adjacent to \(\angle A\). "Adjacent" means "next to." \(BC\) is called the leg opposite \(\angle A\). "Opposite" here means "furthest away from."
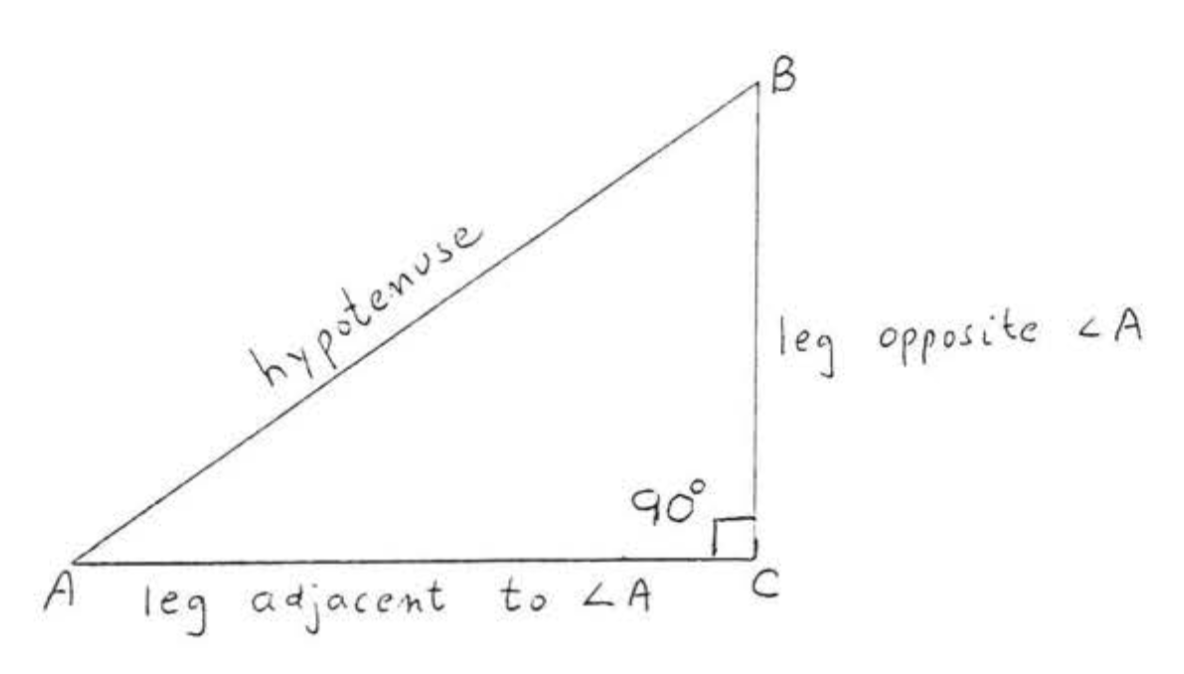
We define the sine, cosine, and tangent of an acute angle \(A\) in a right triangle as follows:
\(\begin{array} {lcl} {\text{sine } A = \dfrac{\text{leg opposite } \angle A}{\text{hypotenuse}}} & \ \ \ & {(\sin A = \dfrac{\text{opp}}{\text{hyp}})} \\ {\text{cosine } A = \dfrac{\text{leg adjacent to } \angle A}{\text{hypotenuse}}} & \ \ \ & {(\cos A = \dfrac{\text{adj}}{\text{hyp}})} \\ {\text{tangent } A = \dfrac{\text{leg opposite } \angle A}{\text{leg adjacent to } \angle A}} & \ \ \ & {(\tan A = \dfrac{\text{opp}}{\text{adj}})} \end{array}\)
The sine, cosine, and tangent are called trigonometric functions.
Find the sine, cosine, and tangent of \(\angle A\):
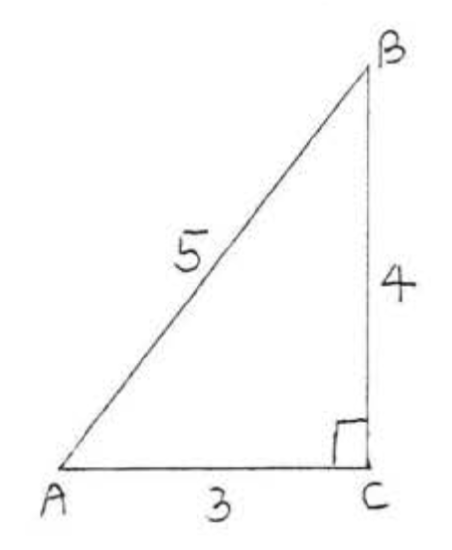
Solution
leg adjacent to \(\angle A = 3\).
leg opposite \(\angle A = 4\).
hypotenuse = 5.
\(\sin A = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{4}{5}\). \(\cos A = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{3}{5}\). \(\tan A = \dfrac{\text{opp}}{\text{adj}} = \dfrac{4}{3}\).
Answer: \(\sin A = \dfrac{4}{5}\), \(\cos A = \dfrac{3}{5}\), \(\tan A = \dfrac{4}{3}\).
Find the sine, cosine, and tangent of \(\angle B\):

Solution
leg adjacent to \(\angle B = 4\).
leg opposite \(\angle B = 3\).
hypotenuse = 5.
\(\sin B = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{3}{5}\). \(\cos B = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{4}{5}\). \(\tan B = \dfrac{\text{opp}}{\text{adj}} = \dfrac{3}{4}\).
Answer: \(\sin B = \dfrac{3}{5}\), \(\cos B = \dfrac{4}{5}\), \(\tan B = \dfrac{3}{4}\).
The definitions of sine, cosine, and tangent should be memorized, It may be helpful to remember the mnemonic "SOHCAHTOA:"
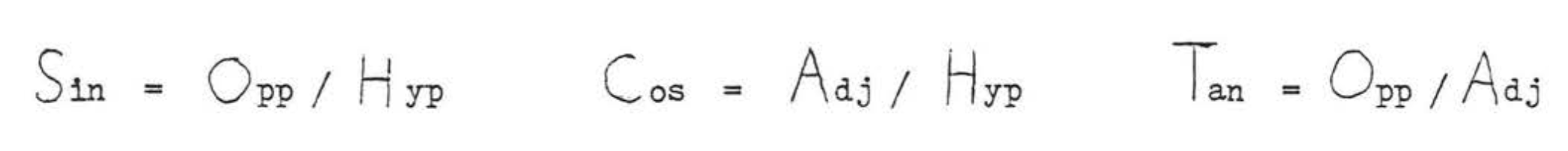
Find \(\sin A\), \(\cos A\), and \(\tan A\):
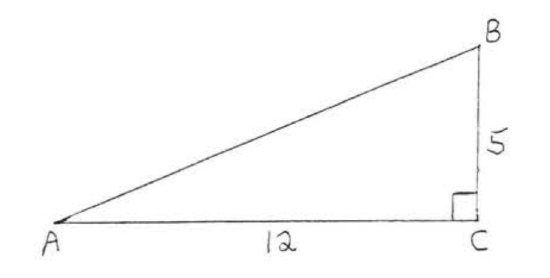
Solution
To find the hypotenuse, we use the Pythagorean Theorem:
\(\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {5^2 + 12^2} & = & {\text{hyp}^2} \\ {25 + 144} & = & {\text{hyp}^2} \\ {169} & = & {\text{hyp}^2} \\ {13} & = & {\text{hyp}} \end{array}\)
\(\sin A = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{5}{13}\). \(\cos A = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{12}{13}\). \(\tan A = \dfrac{\text{opp}}{\text{adj}} = \dfrac{5}{12}\).
Answer: \(\sin A = \dfrac{5}{13}\), \(\cos A = \dfrac{12}{13}\), \(\tan A = \dfrac{5}{12}\).
Find \(\sin A\), \(\cos A\), and \(\tan A\):
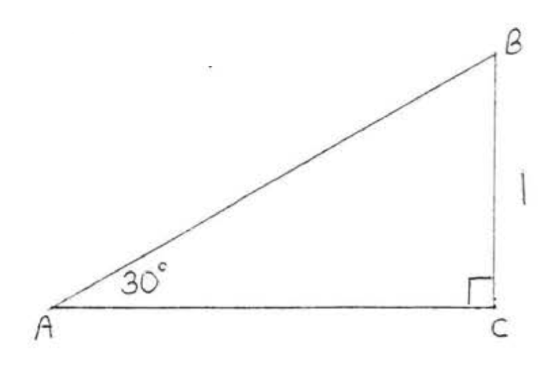
Solution
\(\triangle ABC\) is a \(30^{\circ}-60^{\circ}-90^{\circ}\) triangle so by Theorem 4.5.1, Section 4.5, \(AB = \text{hyp} = 2s = 2(1) = 2\) and \(AC = L = s\sqrt{3} = (1) \sqrt{3} = \sqrt{3}\).
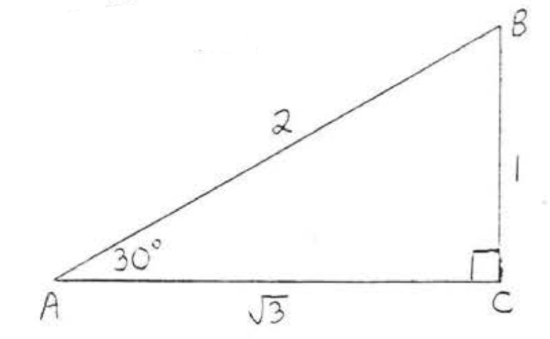
\(\sin A = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{1}{2}\), \(\cos A = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{\sqrt{3}}{2}\),
\(\tan A = \dfrac{\text{opp}}{\text{adj}} = \dfrac{1}{\sqrt{3}} = \dfrac{1}{\sqrt{3}} \dfrac{\sqrt{3}}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}\).
Answer: \(\sin A = \dfrac{1}{2}\), \(\cos A = \dfrac{\sqrt{3}}{2}\), \(\tan A = \dfrac{\sqrt{3}}{3}\).
Find \(\sin D, \cos D\), and \(\tan D\):
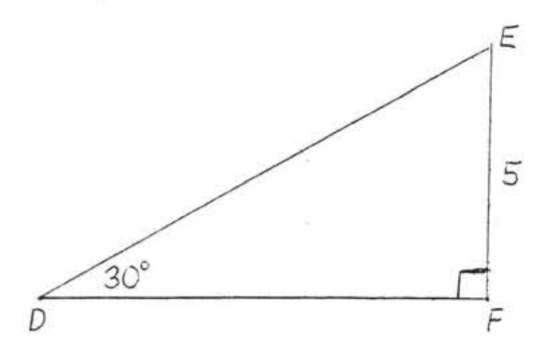
Solution
Again using Theorem 4.5.1, Section 4.5, \(DE = \text{hyp} = 2s = 2(5) = 10\) and \(DF = L = s\sqrt{3} = 5\sqrt{3}\).
\(\sin D = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{5}{10} = \dfrac{1}{2}\), \(\cos D = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{5\sqrt{3}}{10} = \dfrac{\sqrt{3}}{2}\), \(\tan D = \dfrac{\text{opp}}{\text{adj}} = \dfrac{5}{5\sqrt{3}} = \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}\).
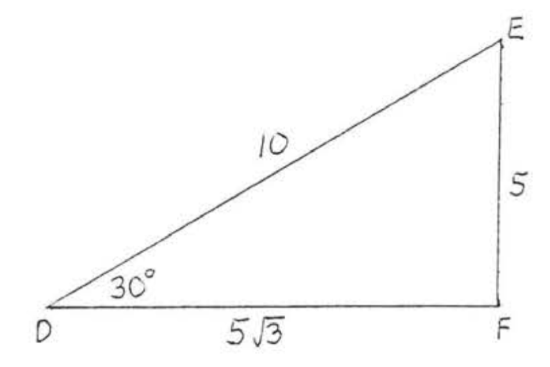
Answer: \(\sin D = \dfrac{1}{2}\), \(\cos D = \dfrac{\sqrt{3}}{2}\), \(\tan D = \dfrac{\sqrt{3}}{3}\).
Notice that the answers to Example \(\PageIndex{4}\) to Example \(\PageIndex{5}\) were the same. This is because \(\angle A = \angle D = 30^{\circ}\). The values of the trigonometric functions for all \(30^{\circ}\) angles will be the same, The reason is that all right triangles with a \(30^{\circ}\) angle are similar. Therefore their sides are proportional and the trigonometric ratios are equal. What holds for \(30^{\circ}\) angles holds for other acute angles as well. We state this in the following theorem:
The values of the trigonometric functions for equal angles are the same.
In Figure \(\PageIndex{3}\), if \(\angle A = \angle D = x^{\circ}\) then \(\sin A = \sin D\), \(\cos A = \cos D\), and \(\tan A = \tan D\).
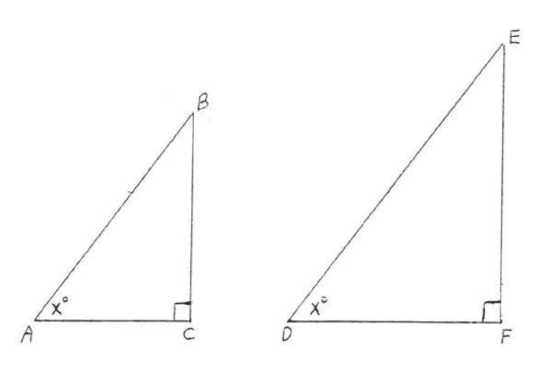
- Proof
-
\(\angle A = \angle D = x^{\circ}\) and \(\angle C = \angle F = 90^{\circ}\) so \(\triangle ABC \cong \triangle DEF\) by \(AA = AA\). Therefore,
\(\dfrac{BC}{EF} = \dfrac{AB}{DE}\) and \(\dfrac{AC}{DF} = \dfrac{AB}{DE}\) and \(\dfrac{BC}{EF} = \dfrac{AC}{DF}\).
By Theorem 4.1.2, Section 4.1, we may interchange the means of each proportion:
\(\dfrac{BC}{AB} = \dfrac{EF}{DE}\) and \(\dfrac{AC}{AB} = \dfrac{DF}{DE}\) and \(\dfrac{BC}{AC} = \dfrac{EF}{DF}\).
These proportions just state that
\(\sin A = \sin D\), and \(\cos A = \cos D\), and \(\tan A = \tan D\).
Theorem \(\PageIndex{1}\) tells us that the trigonometric functions do not depend on the particular triangle chosen, only on the number of degrees in the angle. If we want to find the trigonometric values of an angle, we may chose any right triangle containing the angle which is convenient to use.
If \(\sin A = \dfrac{12}{13}\) find \(\cos A\) and \(\tan A\).
Solution
If \(\sin A = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{12}{13}\) then there is a right triangle \(ABC\) containing \(\angle A\) with leg opposite \(\angle = 12\) and hypotenuse = 13 (see Figure \(\PageIndex{4}\)).
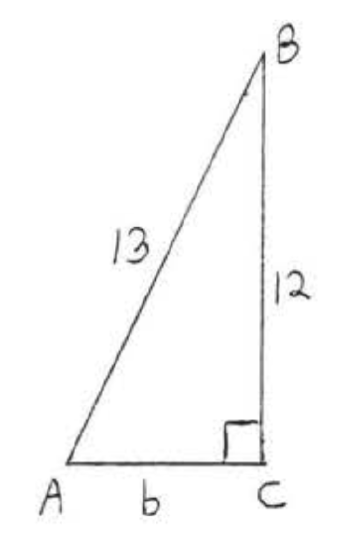
Let \(b =\) leg adjacent to \(\angle A\).
\(\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {b^2 + 12^2} & = & {13^2} \\ {b^2 + 144} & = & {169} \\ {-144} & \ & {-144} \\ {b^2} & = & {25} \\ {b} & = & {5} \end{array}\)
\(\cos A = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{5}{13}\), \(\tan A = \dfrac{\text{opp}}{\text{adj}} = \dfrac{12}{5}\).
Answer: \(\cos A = \dfrac{5}{13}\), \(\tan A = \dfrac{12}{5}\).
If \(\tan A = 2\) find \(\sin A\) and \(\cos A\).
Solution
\(\tan A = \dfrac{\text{opp}}{\text{adj}} = 2 = \dfrac{2}{1}\). Let \(\triangle ABC\) be such that \(a=\) leg opposite \(\angle A = 2\) and \(b =\) leg adjacent to \(\angle A = 1\). See Figure \(\PageIndex{5}\).
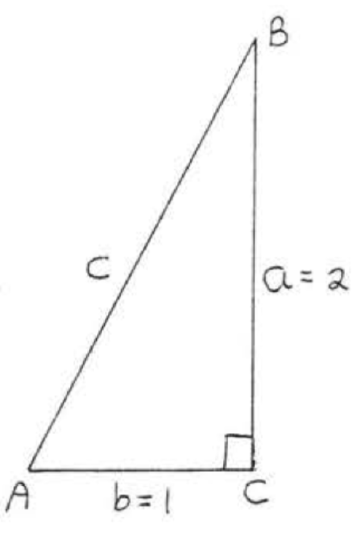
\(\begin{array} {rcl} {a^2 + b^2} & = & {c^2} \\ {2^2 + 1^2} & = & {c^2} \\ {4 + 1} & = & {c^2} \\ {5} & = & {c^2} \\ {\sqrt{5}} & = & {c} \end{array}\)
\(\sin A = \dfrac{\text{opp}}{\text{hyp}} = \dfrac{2}{\sqrt{5}} = \dfrac{2}{\sqrt{5}} \dfrac{\sqrt{5}}{\sqrt{5}} = \dfrac{2\sqrt{5}}{5}\).
\(\cos A = \dfrac{\text{adj}}{\text{hyp}} = \dfrac{1}{\sqrt{5}} = \dfrac{1}{\sqrt{5}} \dfrac{\sqrt{5}}{\sqrt{5}} = \dfrac{\sqrt{5}}{5}\).
Answer: \(\sin A = \dfrac{2\sqrt{5}}{5}\), \(\cos A = \dfrac{\sqrt{5}}{5}\).
Problems
1 - 14. Find \(\sin A, \cos A, \tan A, \sin B, \cos B\), and \(\tan B\):
1.
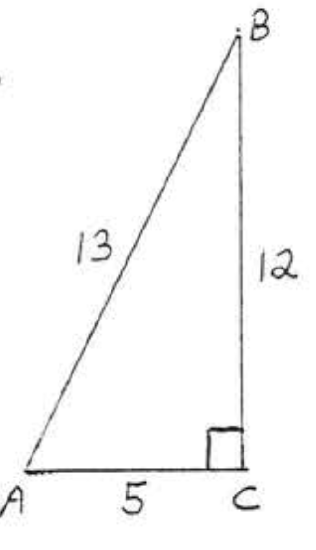
2.
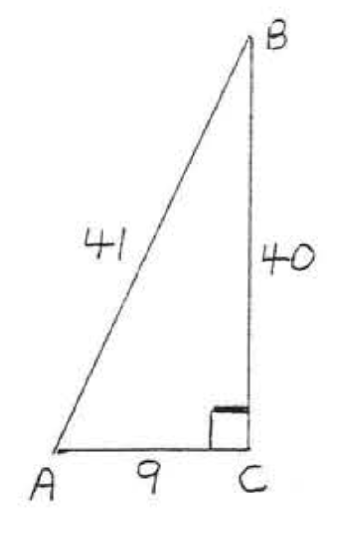
3.
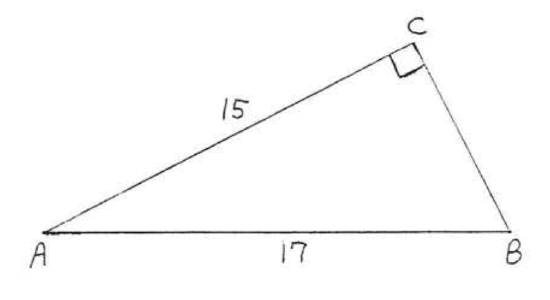
4.
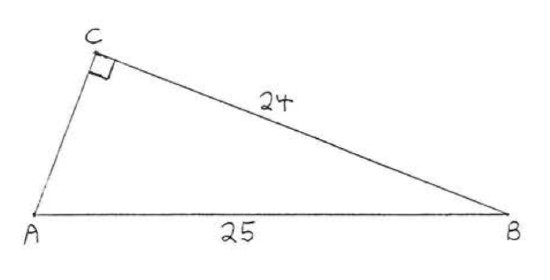
5.
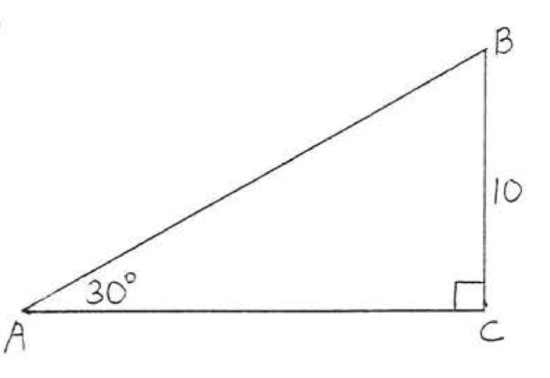
6.
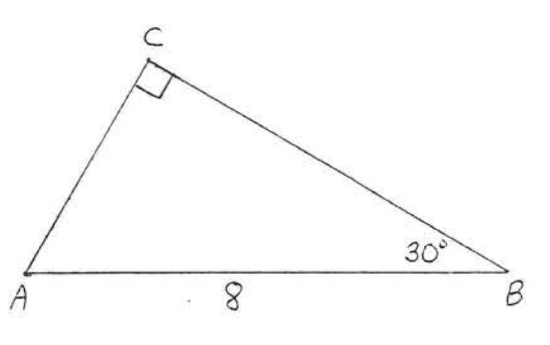
7.
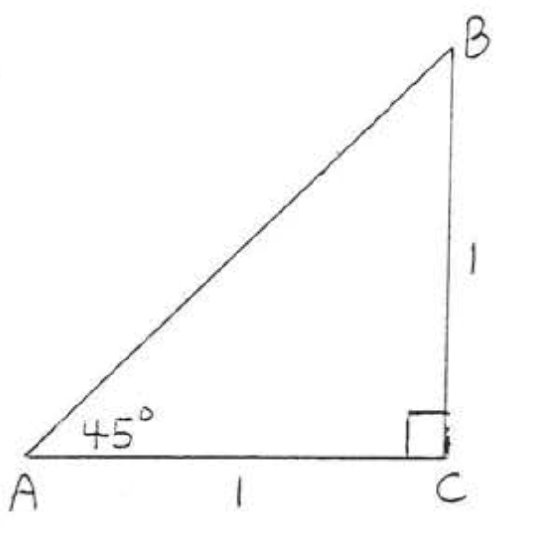
8.
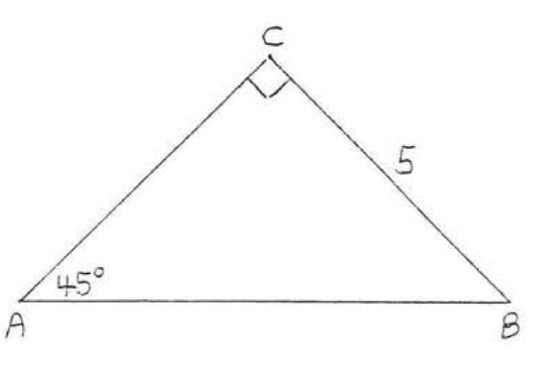
9.
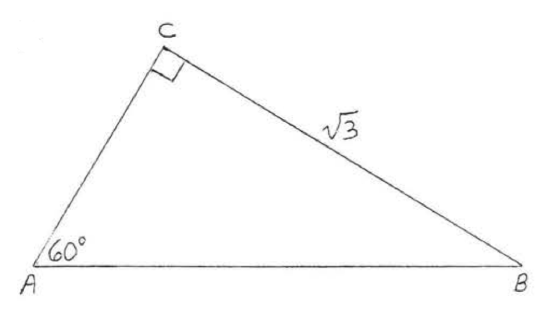
10.
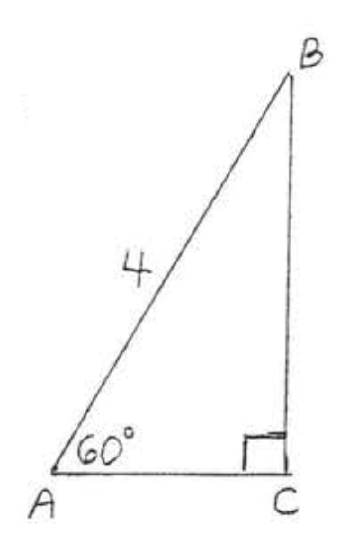
11.
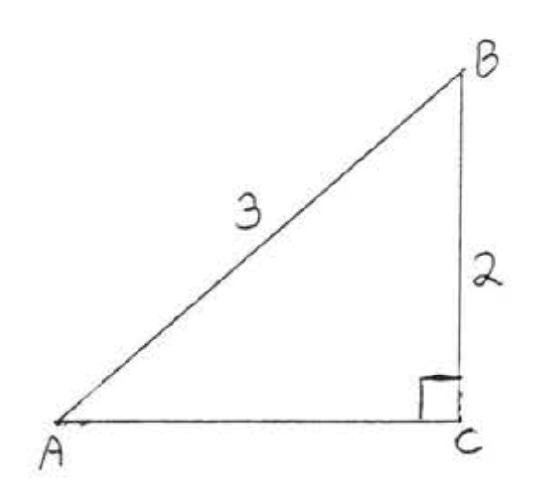
12.
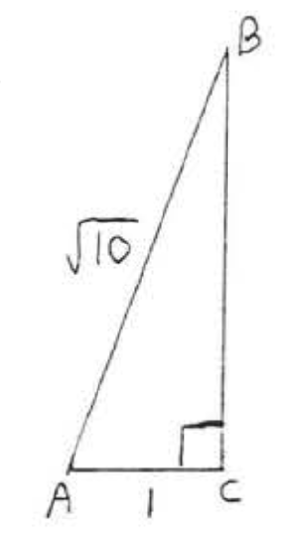
13.
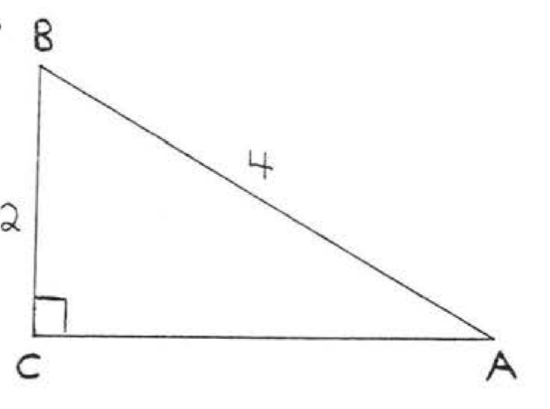
14.
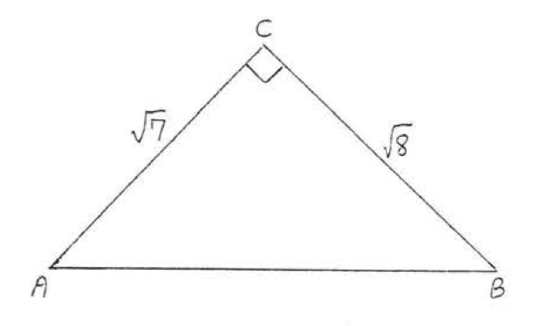
15. If \(\sin A = \dfrac{4}{5}\) find \(\cos A\) and \(\tan A\).
16. If \(\sin A = \dfrac{\sqrt{2}}{2}\) find \(\cos A\) and \(\tan A\).
17. If \(\cos A = \dfrac{\sqrt{3}}{2}\) find \(\sin A\) and \(\tan A\).
18. If \(\cos A = \dfrac{1}{3}\) find \(\sin A\) and \(\tan A\).
19. If \(\tan A = 3\) find \(\sin A\) and \(\cos A\).
20. If \(\tan A = 1\) find \(\sin A\) and \(\cos A\).


