5.2: Solution of Right Triangles
- Page ID
- 34143
In the preceding section we showed that all \(30^{\circ}\) angles have the same trigonometric values. If we compute each of these values to four decimal places, we obtain \(\sin 30^{\circ} = \dfrac{1}{2} = 0.5000\), \(\cos 30^{\circ} = \dfrac{\sqrt{3}}{2} = \dfrac{1.73205}{2} = 0.8660\), and \(\tan 30^{\circ} = \dfrac{\sqrt{3}}{3} = \dfrac{1.73205}{3} = 0.5774\). These numbers appear in the table of trigonometric values on page 356 in the row corresponding to \(30^{\circ}\).
As you can see, this table contains the trigonometric values of angles from \(1^{\circ}\) to \(90^{\circ}.\) It is impractical to compute most of these values directly, so we will use this table when we need them. A pocket calculator with trigonometric functions may also be used.
Find \(\sin 20^{\circ}\), \(\cos 20^{\circ},\), and \(\tan 20^{\circ}\).
Solution
Look for \(20^{\circ}\) in the angle column of the table on page 356:

If you are using a pocket calculator, first make sure that it is in degree mode. Then type in 20 , followed by the sin, cos, or tan keys.
Answer: \(\sin 20^{\circ}=0.3420\), \(\cos 20^{\circ}=0.9397\), \(\tan 20^{\circ}=0.3640\)
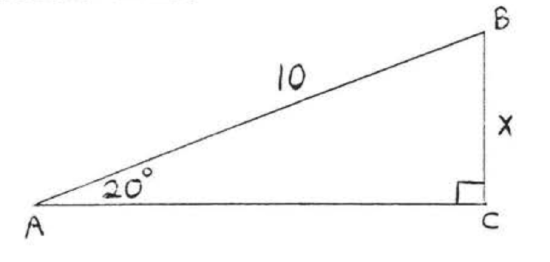
Find \(x\) to the nearest tenth:
Solution
We wish to find the leg opposite \(20^{\circ}\) and we know the hypotenuse. We use the sine because it is the only one of the three trigonometric functions which involves both the opposite leg and the hypotenuse.
\(\begin{array} {rcl} {\sin 20^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {.3420} & = & {\dfrac{x}{10}} \\ {(10)(.3420)} & = & {\dfrac{x}{\cancel{10}} \cancel{(10)}} \\ {3.420} & = & {x} \end{array}\)
If you are using a pocket calculator, type

Answer: \(x = 3.4\)
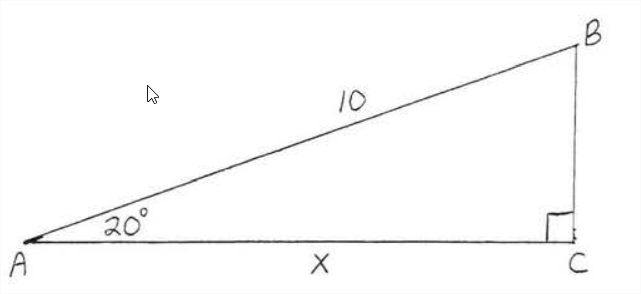
Find \(x\) to the nearest tenth:
Solution
We know the hypotenuse and we wish to find the leg adjacent to \(\angle A\). We therefore use the cosine.
\(\begin{array} {rcl} {\cos 20^{\circ}} & = & {\dfrac{\text{adj}}{\text{hyp}}} \\ {0.9397} & = & {\dfrac{x}{10}} \\ {9.397} & = & {x} \end{array}\)
If you are using a pocket calculator, type

Answer: \(x = 9.4\)
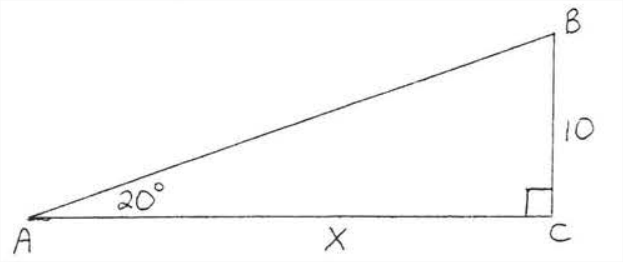
Find \(x\) to the nearest tenth:
Solution
We know the leg opposite \(\angle A\) and we wish to find the leg adjacent to \(\angle A\). We therefore use the tangent.
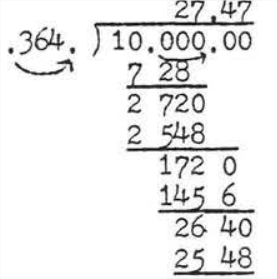
\(\begin{array} {rcl} {\tan 20^{\circ}} & = & {\dfrac{\text{opp}}{\text{adj}}} \\ {.3640} & = & {\dfrac{10}{x}} \\ {(x)(0.3640)} & = & {(\dfrac{10}{\cancel{x}})\cancel{(x)}} \\ {0.3640x} & = & {10} \\ {\dfrac{0.3640 x}{0.3640}} & = & {\dfrac{10}{0.3640}} \\ {x} & = & {\dfrac{10}{0.3640} = \dfrac{10}{0.364} = 27.47} \end{array}\)
27.47 is obtained by long division:
If you are using a pocket calculator, type

Answer: \(x = 27.5\)
There is an easier method to solve Example \(\PageIndex{4}\). \(\angle B = 90^{\circ}-20^{\circ} = 70^{\circ}\) The leg opposite \(\angle B\) is \(x\) and the leg adjacent to \(\angle B\) is 10 .
\(\begin{array} {rcl} {\tan 70^{\circ}} & = & {\dfrac{\text{opp}}{\text{adj}}} \\ {2.7475} & = & {\dfrac{x}{10}} \\ {(2.7475)(10)} & = & {x} \\ {27.475} & = & {x} \\ {27.5} & = & {x} \end{array}\)
This method is easier because it involves multiplication rather than long division.
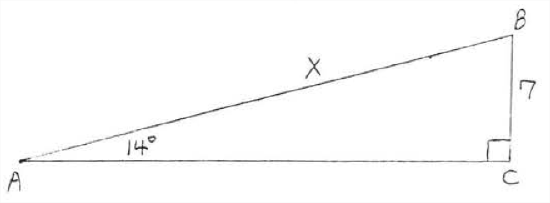
Find \(x\) to the nearest tenth:
Solution
\(\begin{array} {rcl} {\sin 14^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {.2419} & = & {\dfrac{7}{x}} \\ {.2419 x} & = & {7} \\ {x} & = & {\dfrac{7}{.2419} = 28.9} \end{array}\)
In this case there is no way of avoiding long division.(It is possible to avoid long division by introducing tables for the secant and cosecant functions. We will not do so in this book.)
Answer: \(x = 28.9\)
Find \(x\) to the nearest degree:

Solution
\(\begin{array} {rcl} {\sin 14^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {.2419} & = & {\dfrac{7}{x}} \\ {.2419 x} & = & {7} \\ {x} & = & {\dfrac{7}{.2419} = 28.9} \end{array}\)
In this case there is no way of avoiding long division.(It is possible to avoid long division by introducing tables for the secant and cosecant functions. We will not do so in this book.)
Answer: \(x = 28.9\)
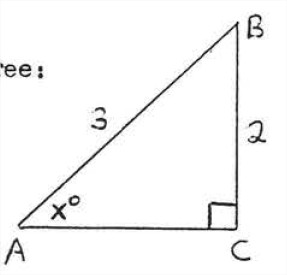
Find \(x\) to the nearest degree:
Solution
\(\begin{array} {rcl} {\sin x^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {\sin x^{\circ}} & = & {\dfrac{2}{3} = .6667} \end{array}\)
In the table we look in the sine column for the value closest to .6667:
| Angle | Sine |
| . | . |
| . | . |
| \(41^{\circ}\) | .6561 |
| \(42^{\circ}\) | .6691 |
| . | . |
.6667 is closest to .6691 because .6691 - .6667 = .0024 whereas .6667 - .6561 = .0106. Therefore \(x^{\circ} = 42^{\circ}\), to the nearest degree.
If you are using a pocket calculator, you will need to use the INV sin or 2nd F sin or SHIFT sin or \(sin^{-1}\) keys, depending on the model of calculatore. Type 2 \(\div\) 3 = INV sin, then round to the nearest degree.
Answer: \(x = 42\)
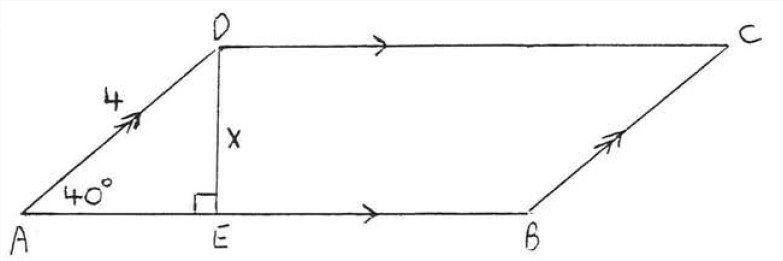
Find \(x\) to the nearest tenth:
Solution
\(\begin{array} {rcl} {\sin 40^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {.6428} & = & {\dfrac{x}{4}} \\ {(4)(.6428)} & = & {\dfrac{x}{\cancel{4}} (\cancel{4})} \\ {2.5712} & = & {x} \\ {2.6} & = & {x} \end{array}\)
Answer: \(x = 2.6\).
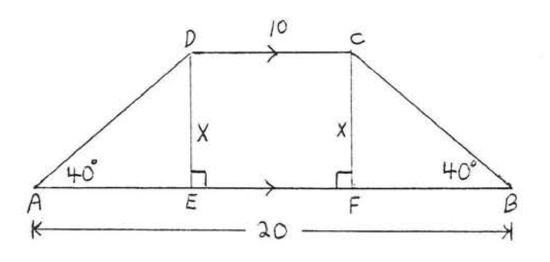
Find \(x\) and \(y\) to the nearest tenth:
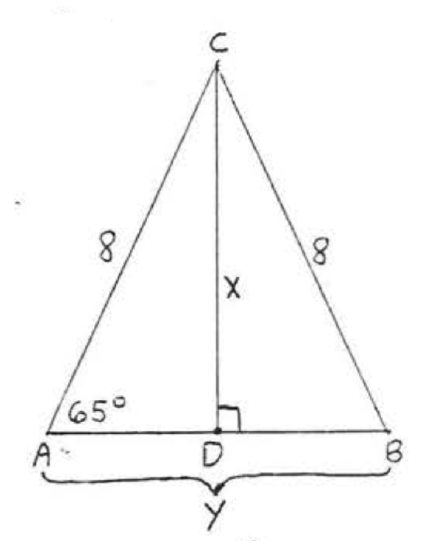
Solution
\(\begin{array} {rcl} {\sin 65^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {.9063} & = & {\dfrac{x}{8}} \\ {(8)(.9063)} & = & {\dfrac{x}{\cancel{8}} (\cancel{8})} \\ {7.2504} & = & {x} \\ {7.3} & = & {x} \end{array}\)
To find \(y\) we first find \(AD\):
\(\begin{array} {rcl} {\cos 65^{\circ}} & = & {\dfrac{\text{adj}}{\text{hyp}}} \\ {.4226} & = & {\dfrac{AD}{8}} \\ {(8)(.4226)} & = & {\dfrac{AD}{8} (8)} \\ {3.3808} & = & {AD} \end{array}\)
Since \(AC = BC = 8\) we have \(\angle A = \angle B = 65^{\circ}\). Therefore \(BD = AD = 3.3808\). \(y = AD + BD = 3.3808 + 3.3808 = 6.7616 = 6.8\).
Answer: \(x = 7.3, y = 6.8\).
The first table of trigonometric values was constructed by the Greek astronomer Hipparchus (c. 180-125 B.C.). Hipparchus assumed the vertex of each angle to be the center of a circle, as \(\angle AOB\) is shown to be in the circle of Figure \(\PageIndex{1}\). Depending on the number of degrees in \(\angle AOB\), his table would give the length of the chord \(AB\) relative to the radius of the circle. Today we would measure \(\angle AOC\) instead of \(\angle AOB\) and use the half chord \(AC\) instead of \(AB\). The ratio \(\dfrac{AC}{AO}\) is then just the sine of \(\angle AOC\).
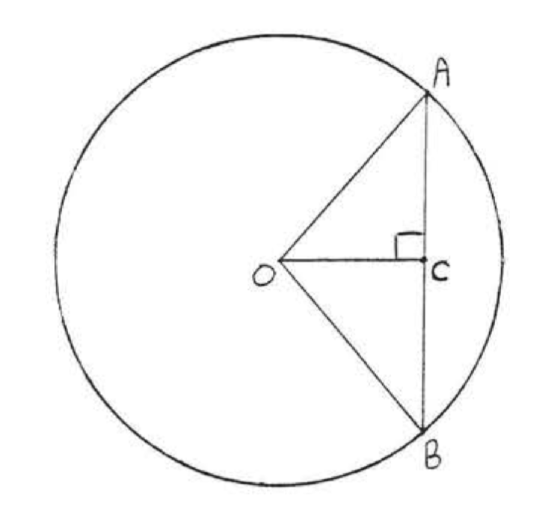
Hipparchus obtained some of the values for his table from the properties of special geometric figures, such as the \(30^{\circ}-60^{\circ}-90^{\circ}\) triangle and the \(45^{\circ}-45^{\circ}-90^{\circ}\) triangle. The rest of the values were obtained from those already known by using trigonometric identities and approximation. The identities he used were essentially the half-angle and sum and difference formulas which students encounter in modern trigonometrJ courses.
The trigonometry of the Greeks, and later of the Hindus and the Arabs, was based primarily on the sine function. The Hindus replaced the table of chords of Hipparchus with a table of half chords. The term sine is derived from a Hindu word meaning "half-chord."
Gradually the right triangle replaced the chords of circles as the basis of trigonometric definitions. The cosine is just the sine of the complement of the angle in a right triangle, For example the complement of \(60^{\circ}\) is \(30^{\circ}\) and \(\cos 60^{\circ} = \sin 30^{\circ} = .5\).
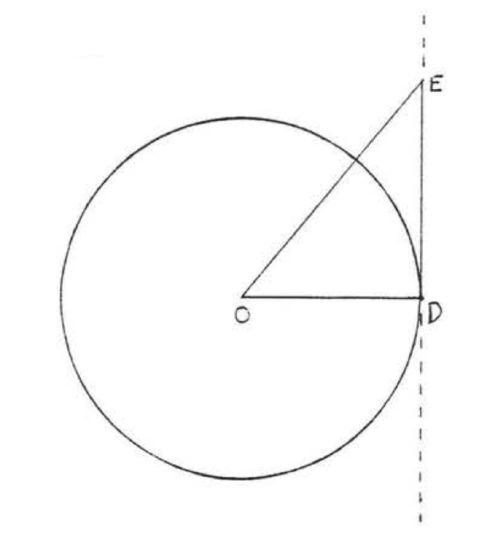
A tangent is a line which touches a circle at only one point (see Chapter 7). In trigonometry it refers to just that part of the tangent line intercepted by the angle, relative to the radius of the circle. In Figure \(\PageIndex{2}\) the tangent of \(\angle DOE\) is the segment \(DE\) divided by the radius \(OD\). The ancient Greeks were probably aware of the tangent function but the first known table of values was constructed by the Arabs in 10th century. The term "tangent" was adopted in the 16th century.
Modern trigonometric tables are constructed from infinite series. These were first discovered in the 17th century by Newton, Leibniz and others. For example the infinite series for the sine function is
\[\sin x = x - \dfrac{x^3}{6} + \dfrac{x^5}{120} - \dfrac{x^7}{5040} + \cdots\]
where \(x\) is in radians, 1 radian = 57.296 degrees. A good approximation of the sine of an angle can be obtained from the infinite series by summing just the first few tenns. This is also the method computers and pocket calculators use to find trigonometric values. The derivation of these formulas is found in calculus textbooks.
Problems
1 - 10. Find each of the following using the table:
1. \(\sin 10^{\circ}\)
2. \(\sin 30^{\circ}\)
3. \(\cos 80^{\circ}\)
4. \(\cos 60^{\circ}\)
5. \(\tan 45^{\circ}\)
6. \(\tan 60^{\circ}\)
7. \(\sin 18^{\circ}\)
8. \(\cos 72^{\circ}\)
9. \(\tan 50^{\circ}\)
10. \(\tan 80^{\circ}\)
11 - 30. Find \(x\) to the nearest tenth:
11.
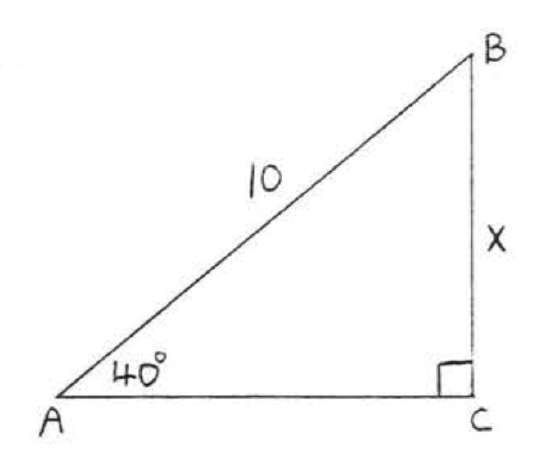
12.
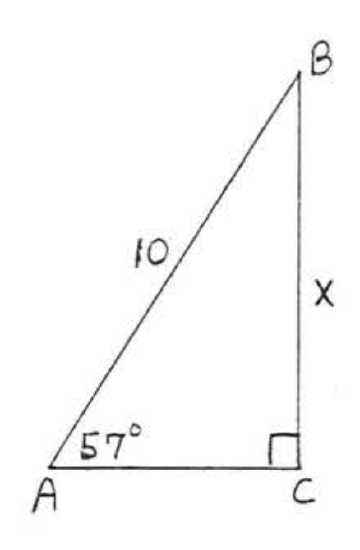
13.
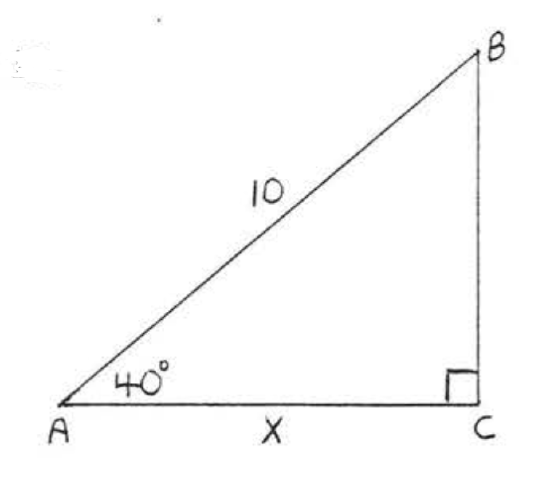
14.
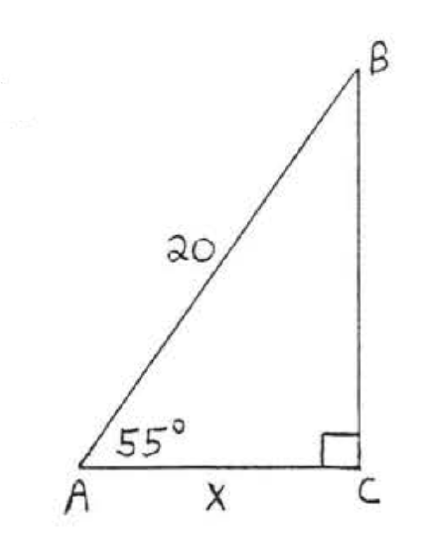
15.
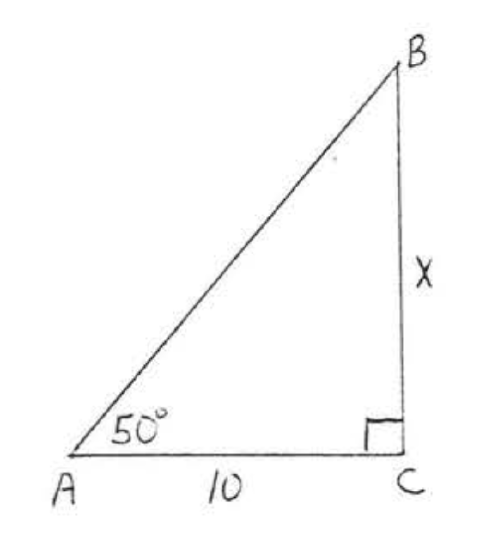
16.
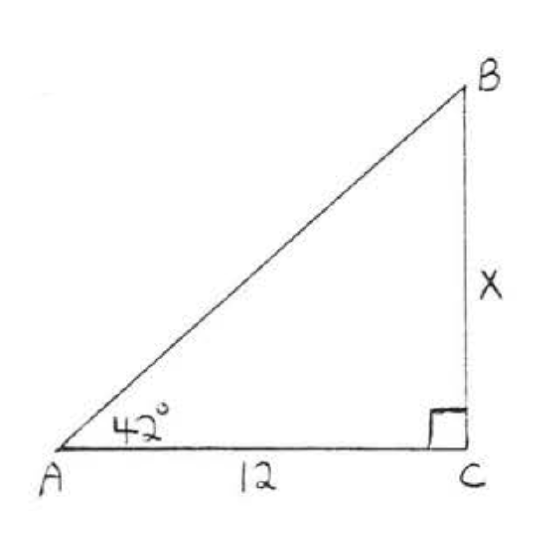
17.
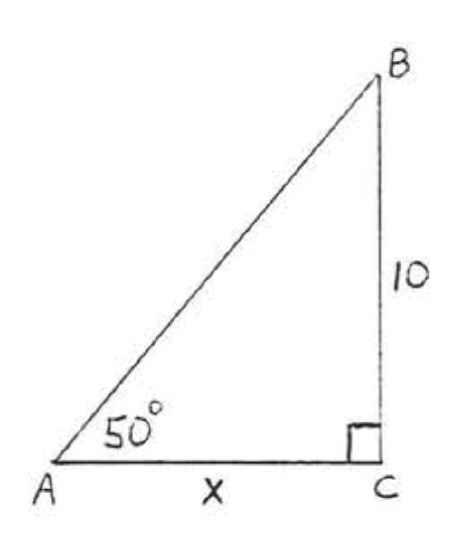
18.
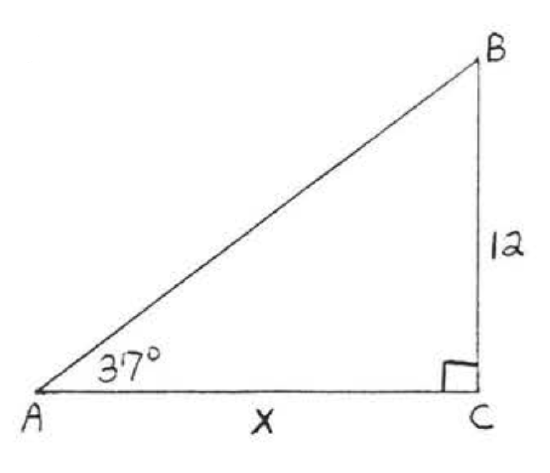
19.
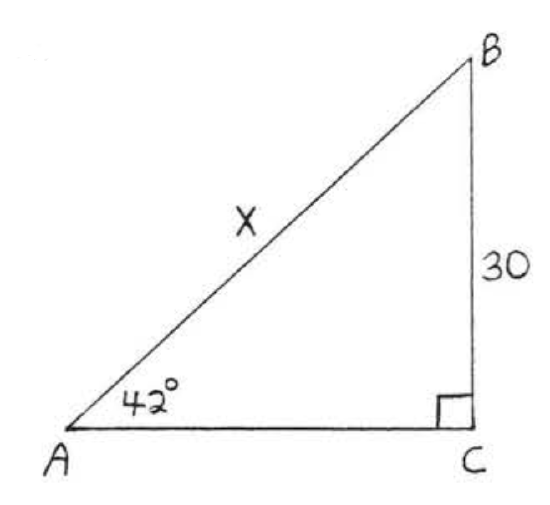
20.
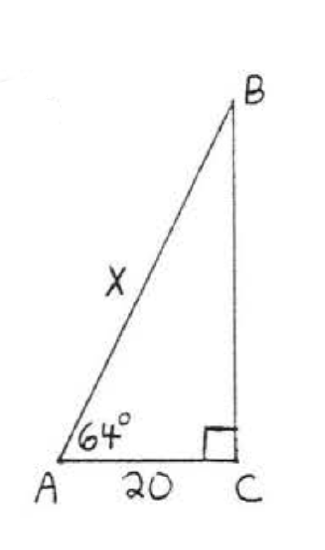
21.
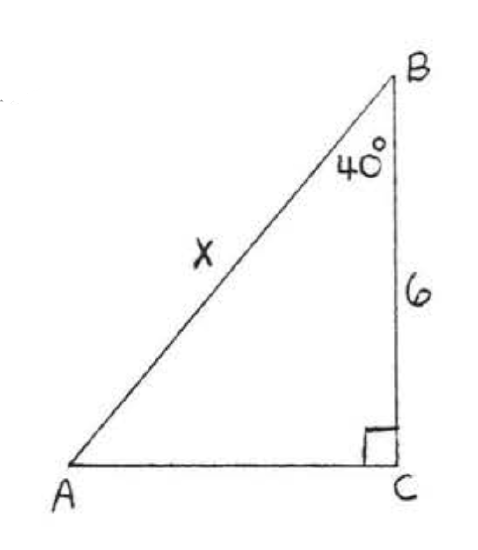
22.
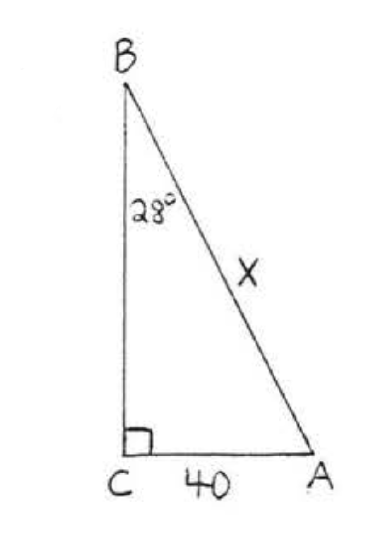
23.
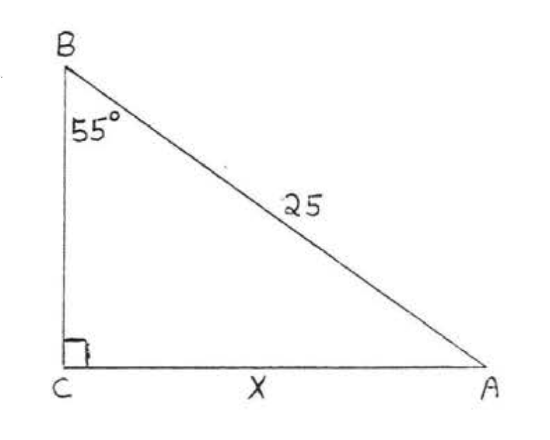
24.
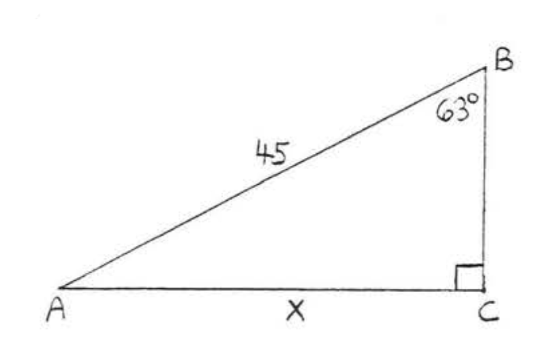
25.
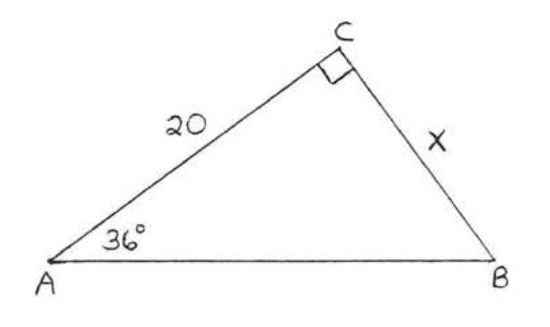
26.
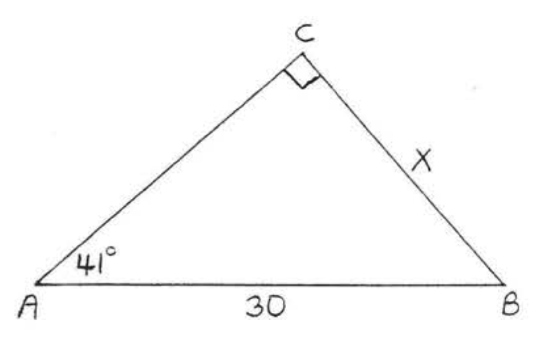
27.
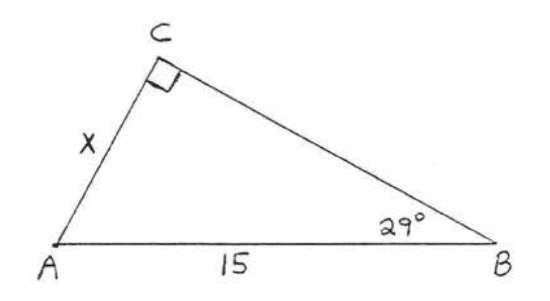
28.
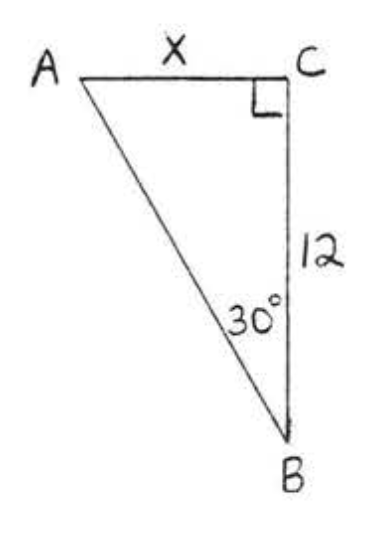
29.
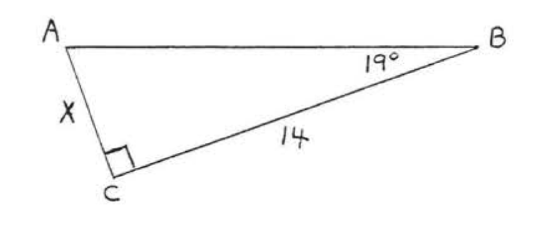
30.
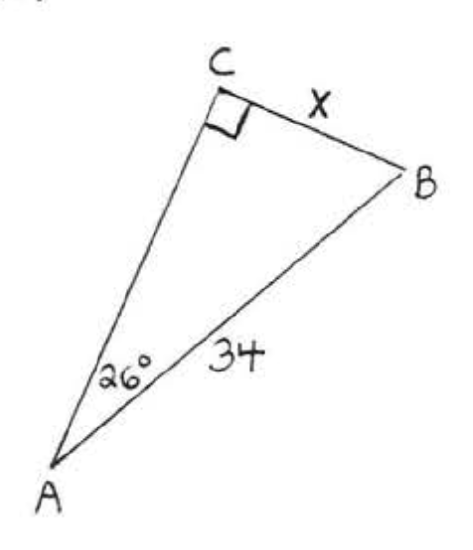
31 - 38. Find \(x\) to the nearest degree:
31.
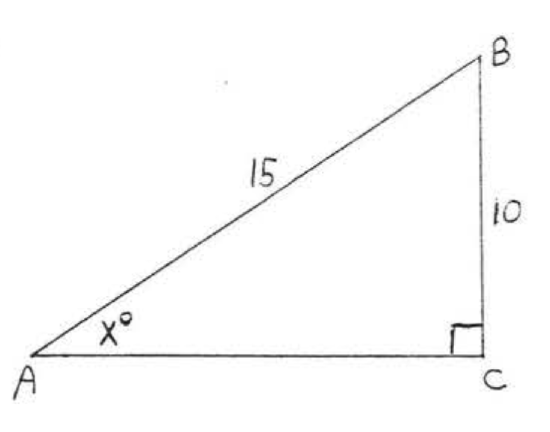
32.
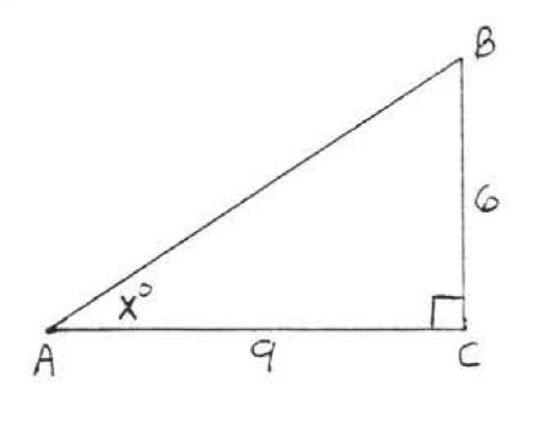
33.
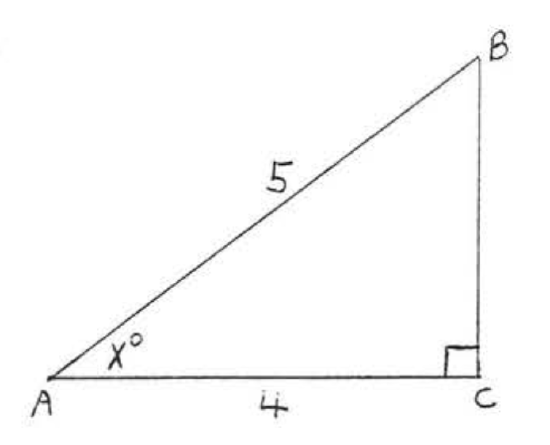
34.
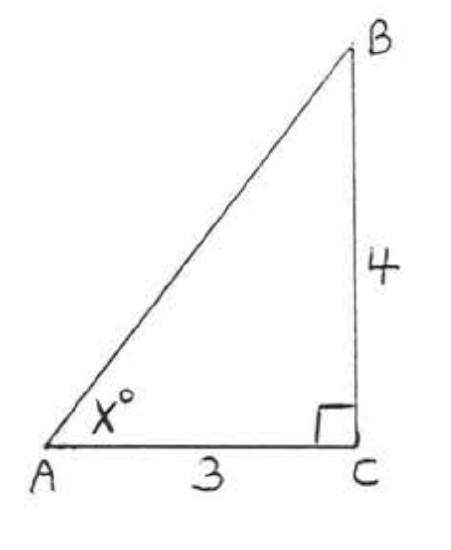
35.
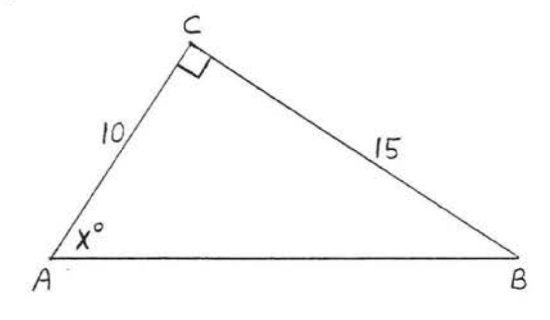
36.
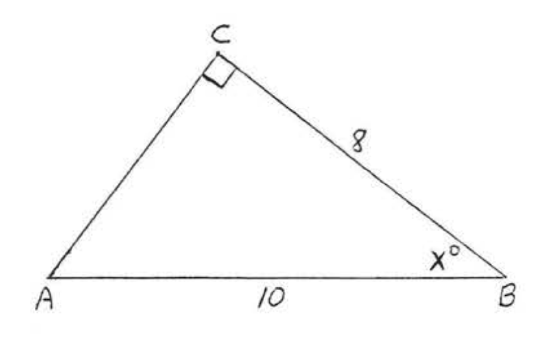
37.
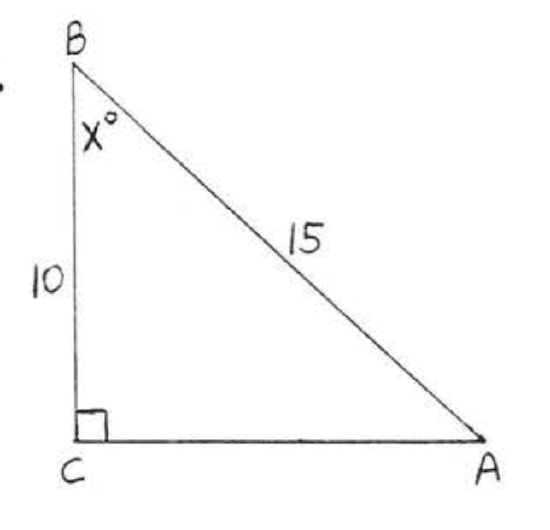
38.
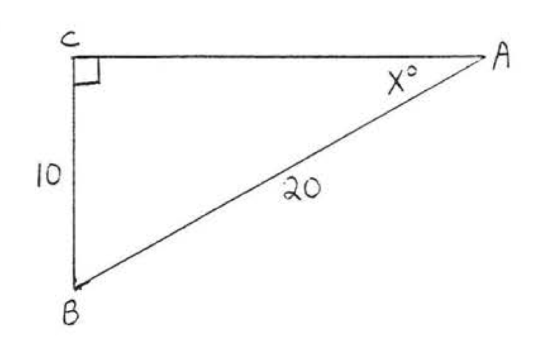
39 - 46. Find \(x\) or \(x\) and \(y\) to the nearest tenth:
39.
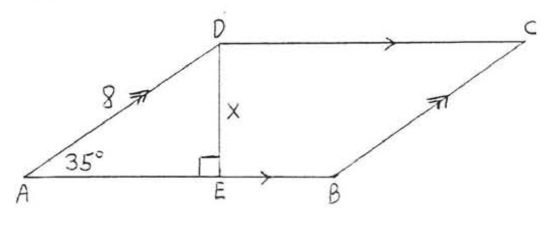
40.
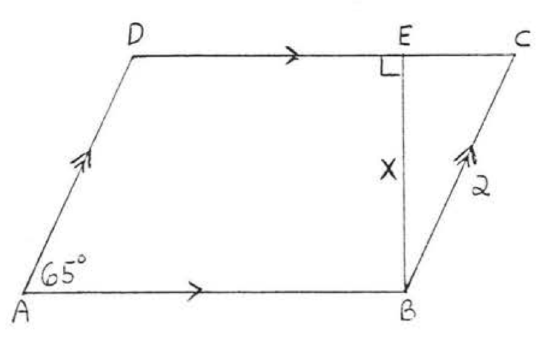
41.
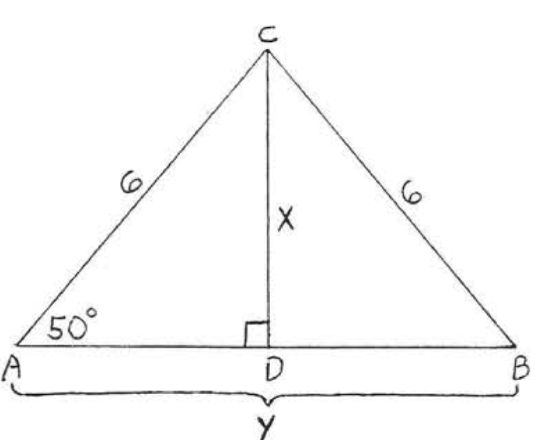
42.
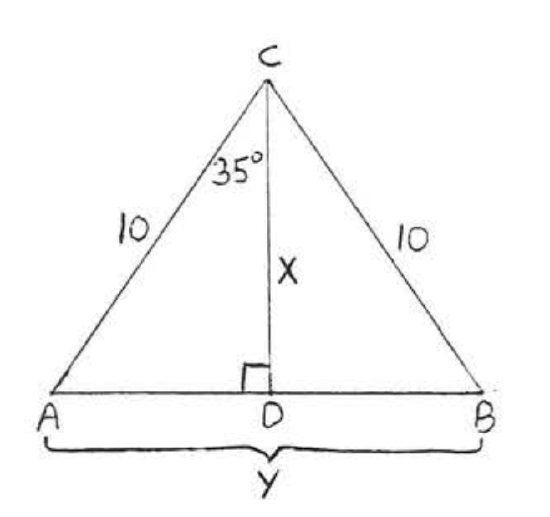
43.
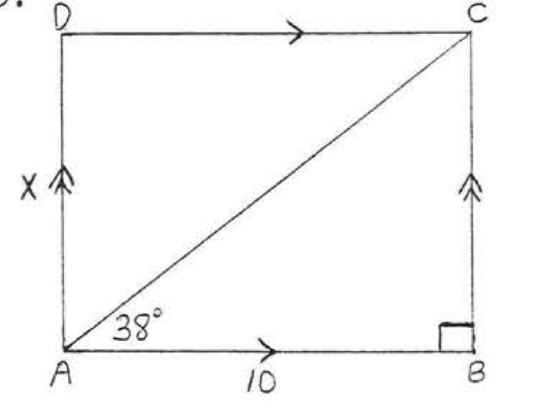
44.
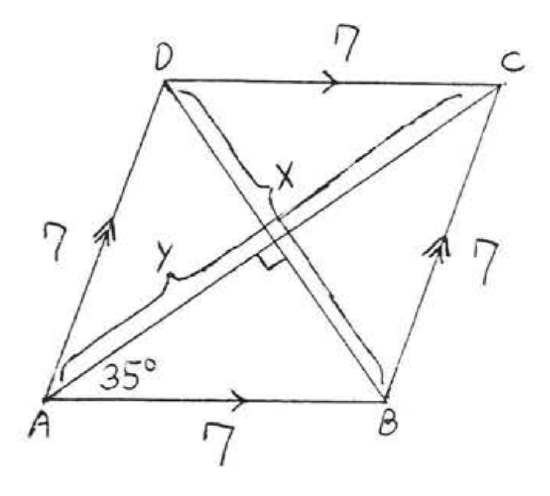
45.
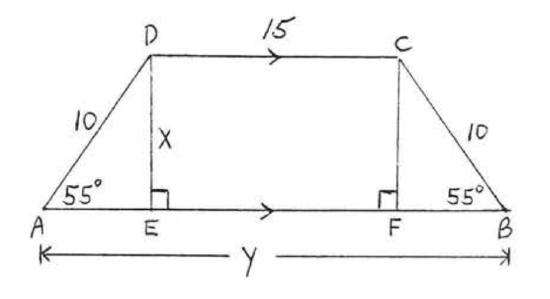
46.